2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》填空题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》填空题专题训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 438.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》填空题专题训练(附答案)
1.如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且=,作∠ACB的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为 .
2.如图,四边形ABCD中,点E、F分别为AD、BC的中点,延长FE交CD延长线于点G,交BA延长线于点H,若∠BHF与∠CGF互余,AB=4,CD=6,则EF的长为 .
3.如图,在△ABC中,E是AB的中点,D是AC上一点,连接DE,BH⊥AC于H,若2∠ADE=90°﹣∠HBC,AD:BC=4:3,CD=2,则BC的长为 .
4.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点,连接AF,BF,∠AFB=90°.已知AB=6,BC=10,则EF的长是 .
5.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=13,AC=8,则DF的长为 .
6.如图,在四边形ABCD中,AB∥CD,AD∥BC,点E为CD上一点且DE=3EC,点F,G分别是AE,BE的中点,若FG=4cm,则DE的长度为 .
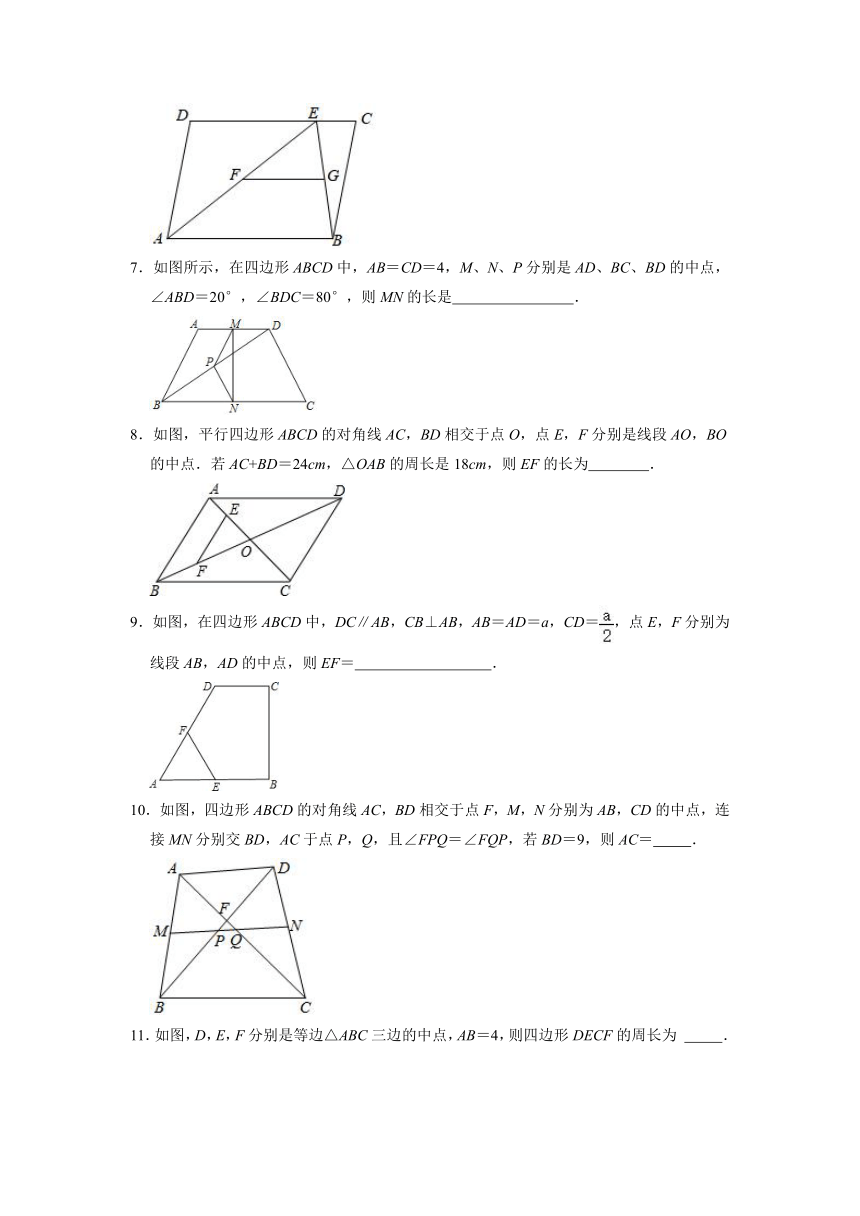
7.如图所示,在四边形ABCD中,AB=CD=4,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=80°,则MN的长是 .
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为 .
9.如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF= .
10.如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC= .
11.如图,D,E,F分别是等边△ABC三边的中点,AB=4,则四边形DECF的周长为 .
12.如图已知,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,连接MN,如果AB=10,BC=15.MN=3,那么△ABC的周长是 .
13.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
14.如图,在△ABC中,E、F、G、H分别为AB、AC、DC、BD的中点,若AD=3,BC=8,则四边形EFGH的周长是 .
15.如图,在△ABC中,AB2﹣BC2=AC2,点D是边BC上一点,点E、F分别是AB、AD的中点.若AB=12,AD=10,EF=2,则△CEF的周长是 .
16.如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠BEF= 度.
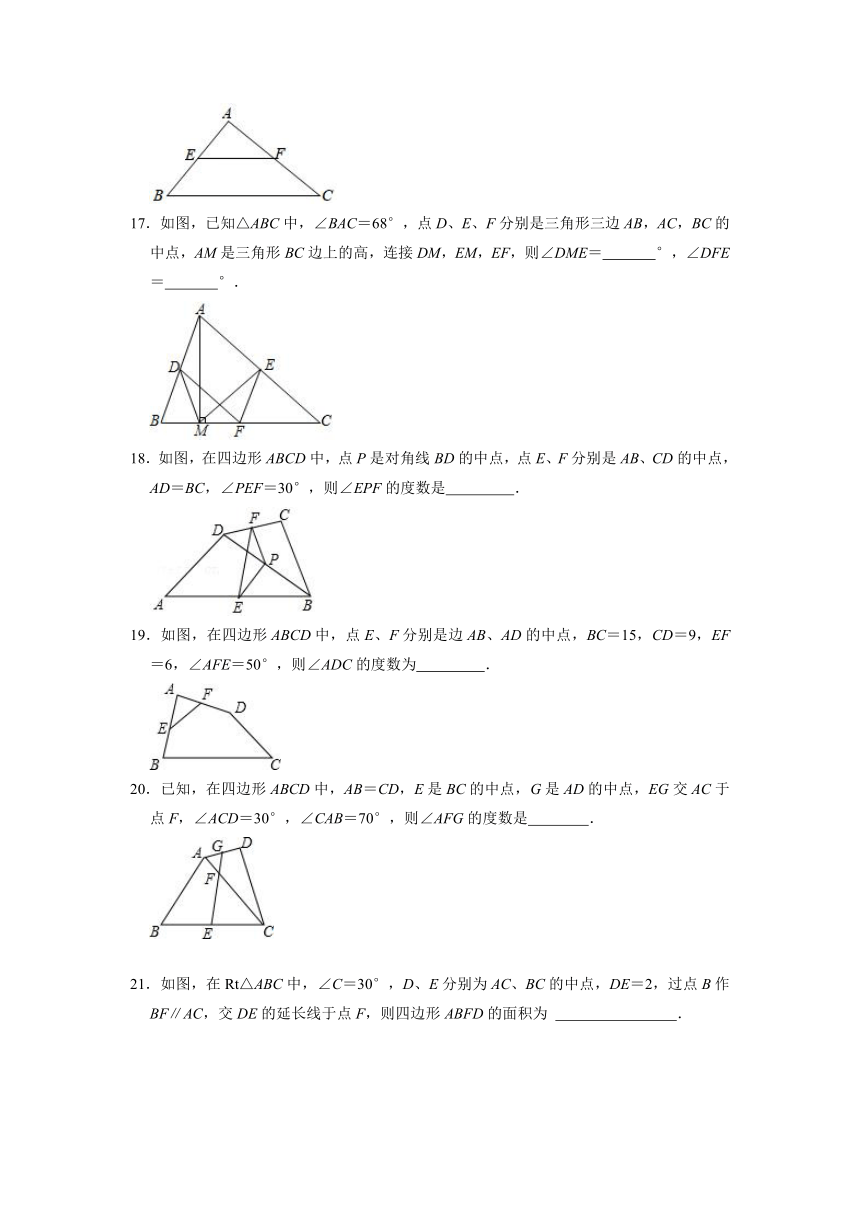
17.如图,已知△ABC中,∠BAC=68°,点D、E、F分别是三角形三边AB,AC,BC的中点,AM是三角形BC边上的高,连接DM,EM,EF,则∠DME= °,∠DFE= °.
18.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
19.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,则∠ADC的度数为 .
20.已知,在四边形ABCD中,AB=CD,E是BC的中点,G是AD的中点,EG交AC于点F,∠ACD=30°,∠CAB=70°,则∠AFG的度数是 .
21.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
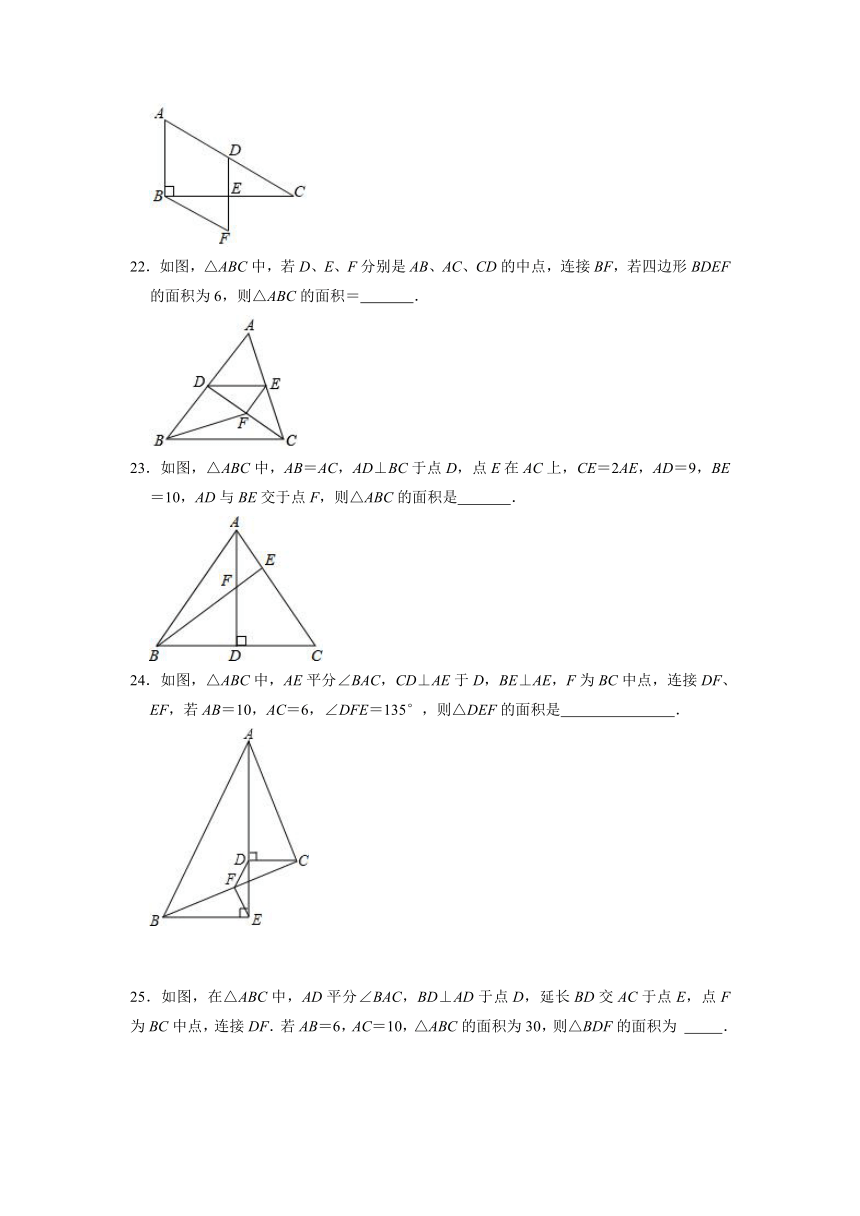
22.如图,△ABC中,若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF的面积为6,则△ABC的面积= .
23.如图,△ABC中,AB=AC,AD⊥BC于点D,点E在AC上,CE=2AE,AD=9,BE=10,AD与BE交于点F,则△ABC的面积是 .
24.如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连接DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是 .
25.如图,在△ABC中,AD平分∠BAC,BD⊥AD于点D,延长BD交AC于点E,点F为BC中点,连接DF.若AB=6,AC=10,△ABC的面积为30,则△BDF的面积为 .
26.如图,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.若AD、BC所在直线互相垂直,的值为 .
27.如图,已知E是AC的中点,C是BD的中点,那么= .
28.如图,点D为△ABC的边AC的中点,点E为AB上一点,若∠AED=150°,∠ABC=120°,则的值为 .
29.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD的值为 .
参考答案
1.解:∵DC=AC=10,∠ACB的平分线CF交AD于F,
∴F为AD的中点,CF⊥AD,
∴∠CFD=90°,
∵DC=10,CF=8,
∴DF==6,
∴AD=2DF=12,
∵=,
∴BD=8,
∵点E是AB的中点,
∴EF为△ABD的中位线,
∴EF=BD=4,
故答案为:4.
2.解:连接BD,取BD的中点M,连接EM,FM,
∵E、F分别为AD、BC的中点,M为BD的中点,
∴EM,MF分别为△ADB、△BCD的中位线,
∴EM∥AB,MF∥DC,EM=AB=2,MF=DC=3,
∵MF∥DC,
∴∠BFM=∠BCD,
∵∠FGC+∠GCF=∠BFH=∠BFM+∠EFM,
∴∠FGC=∠EFM,
∵EM∥AB,
∴∠FEM=∠FHB,
∵∠BHF与∠CGF互余,
∴∠CGF+∠BHF=∠EFM+∠FEM=90°,
∴∠EMF=180°﹣∠EFM﹣∠FEM=90°,
∴△EMF是直角三角形,
∴EF=,
故答案为:.
3.解:如图,延长AC至N,使CN=BC,连接BN,
∵2∠ADE=90°﹣∠HBC,∠BCA=90°﹣∠HBC,
∴∠BCA=2∠ADE,
∵CN=BC,
∴∠N=∠CBN,
∴∠BCA=∠N+∠CBN=2∠N,
∴∠ADE=∠N,
∴DE∥BN,
又∵E是AB的中点,
∴DE是△ABN的中位线,
∴AD=DN,
∵AD:BC=4:3,
∴设AD=DN=4x,BC=CN=3x,
∴CD=DN﹣CN=x=2,
∴BC=6,
故答案为6.
4.解:∵点D,E分别是边AB,AC的中点,BC=10,
∴DE=BC=5,
在Rt△AFB中,点D是边AB的中点,AB=6,
∴DF=AB=3,
∴EF=DE﹣DF=5﹣3=2,
故答案为:2.
5.解:延长CF交AB于点G,
∵AE平分∠BAC,
∴∠GAF=∠CAF,
∴AF垂直平分CG,
∴AC=AG,
GF=CF,
又∵点D是BC中点,
∴DF是△CBG的中位线,
∴DF=BG=(AB﹣AG)=(AB﹣AC)=2.5,
故答案为:2.5.
6.解:如图,在四边形ABCD中,AB∥CD,AD∥BC,则四边形ABCD是平行四边形,故AB=CD.
∵点F,G分别是AE,BE的中点,
∴FG是△AEB的中位线.
∴AB=2FG=8cm.
∴CD=AB=8cm.
∵DE=3EC,
∴DE=6cm.
故答案是:6cm.
7.解:作PH⊥MN于H,
∵M、N、P分别是AD、BC、BD的中点,
∴PM=AB=2,PN=CD=2,PM∥AB,PN∥CD,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=80°,PM=PN,
∴∠MPN=120°,
∵PM=PN,
∴∠PMN=30°,MH=HN,
∴PH=PM=1,
由勾股定理得,MH==,
∴MN=2MH=2,
故答案为:2.
8.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24厘米,
∴OA+OB=12cm,
∵△OAB的周长是18厘米,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3cm.
故答案为:3cm.
9.解:连接DE,
∵四边形ABCD为直角梯形,AB=AD=a,CD=,CB⊥AB,点E,F分别为线段AB,AD的中点
∴△AED为直角三角形.则EF是Rt△AED斜边上的中线,
由直角三角形斜边上的中线等于斜边的一半得,EF=DE=AB=.
故答案为:
10.解:取线段BC的中点E,连接EM、EN,如图所示.
∵M、N,E分别为AB,CD,BC的中点,
∴ME∥AC,ME=AC,NE∥BD,NE=BD=,
∴∠EMN=∠FQP,∠ENM=∠FPQ.
又∵∠FPQ=∠FQP,
∴∠EMN=∠ENM.
∴ME=NE=.
∴AC=2ME=9.
故答案为:9.
11.解:∵△ABC为等边三角形,AB=4,
∴AC=BC=AB=4,
∵D,E,F分别是等边△ABC三边的中点,
∴DF=BC=2,EC=BC=2,DE=AC=2,FC=AC=2,
∴四边形DECF的周长=2+2+2+2=8,
故答案为:8.
12.解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=10,BN=ND,
∵BM=MC,
∴DC=2MN=6,
∴AC=AD+DC=16,
∴△ABC的周长=AB+BC+AC=10+15+16=41,
故答案为:41.
13.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=3,
∴DE=2MN=6,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=22,
∴△ABC的周长=AB+AC+BC=22+16=38,
故答案为:38.
14.解:∵E、F分别为AB、AC的中点,
∴EF=BC=4,
同理可得,FG=AD=1.5,GH=BC=4,EH=AD=1.5,
∴四边形EFGH的周长=4+1.5+4+1.5=11,
故答案为:11.
15.解:∵AB2﹣BC2=AC2,
∴∠ACB=90°,
∵点E、F分别是AB、AD的中点,AB=12,AD=10,
∴CE=AB=6,CF=AD=5,
∵EF=2,
∴△CEF的周长=CE+CF+EF=13,
故答案为:13.
16.解:∵E是AB的中点,F是AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,
∴∠BEF=180°﹣∠B=180°﹣50°=130°,
故答案为:130.
17.解:∵∠BAC=68°,
∴∠B+∠C=180°﹣68°=112°,
∵AM是三角形BC边上的高,
∴∠AMB=∠AMC=90°,
在Rt△AMB中,D是AB的中点,
∴DM=AB=DB,
∴∠DMB=∠B,
同理可得,∠EMC=∠C,
∴∠DMB+∠EMC=∠B+∠C=112°,
∴∠DME=180°﹣(∠DMB+∠EMC)=68°,
∵点D、E、F分别是三角形三边AB,AC,BC的中点,
∴DF、EF分别是△ABC的中位线,
DF∥AC,EF∥AB,
∴∠DFB=∠C,∠EFC=∠B,
∴∠DFB+∠EFC=∠B+∠C=112°,
∴∠DFE=180°﹣(∠DFB+∠EFC)=68°,
故答案为:68;68.
18.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
19.解:连接BD,
∵E、F分别是边AB、AD的中点,
∴EF∥BD,BD=2EF=12,
∴∠ADB=∠AFE=50°,
BD2+CD2=225,BC2=225,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=140°,
故答案为:140°.
20.解:取AC的中点M,连接GM、EM,
∵G是AD的中点,E是BC 的中点,
∴GM是△ADC的中位线,EM是△ABC的中位线,
∴GM=DC,EM=,GM∥CD,EM∥AB,
∵AB=CD,
∴GM=EM,
∴∠GEM=∠EGM,
∵EM∥AB,
∴∠EMC=∠BAC=70°,
∴∠AME=180°﹣70°=110°,
∵GM∥CD,
∴∠AMG=∠ACD=30°,
∴∠EMG=110°+30°=140°,
∴∠EGM==20°,
∴∠AFG=∠EGM+∠AMG=20°+30°=50°,
故答案为50°.
21.解:∵D、E分别为AC、BC的中点,
即DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴AB=2DE,DF∥AB,
又∵BF∥AC,
∴BF∥AD,
∴四边形ABFD是平行四边形,
∵AB⊥BE,
∴S平行四边形ABFD=AB BE,
∵DE=2,
∴AB=2×2=4,
在Rt△ABC中,
∵∠C=30°,
∴AC=2AB=2×4=8,
∴BC===4,
∴BE=BC=2,
∴S平行四边形ABFD=4×2=8,
故答案为8.
22.解:∵点F是CD的中点,
∴S△DEF=S△CEF,
设S△DEF=S△CEF=x,
∵D、E分别是AB、AC的中点,
∴S△ADE=S△CDE=2x,S△BDC=S△ADC=4x,S△BDF=2x,
∴S 四边形BDEF=3x.
∵S 四边形BDEF=6,
∴3x=6,
∴x=2,
∴S△ABC=2S△BDC=8x=16,
故答案为:16.
23.解:如图,取CE的中点G,连接DG.
∵△ABC中,AB=AC,AD⊥BC,
∴BD=CD,即点D是BC的中点,
∴GD是△BCE的中位线,
∴DG∥BE,DG=BE=5.
又∵CE=2AE,
∴AE=GE,即点E是AG的中点,
∴点F是AD的中点,
∴AF=DF=4.5,EF是△ADG的中位线,
∴EF=DG=2.5,
∴BF=BE﹣EF=7.5.
则在直角△BFD中,由勾股定理易求BD=6.
∴BC=12.
则△ABC的面积是:BC AD=×12×9=54.
故答案是:54.
24.解:延长CD交AB于M,延长AC、BE交于点N,作EH⊥DF交DF的延长线于H.
∵AD⊥CM,
∴∠ADC=∠ADM=90°,
∵∠DAM=∠DAC,∠DAM+∠AMC=90°,∠DAC+∠ACM=90°,
∴∠AMC=∠ACM,
∴AM=AC=6,同理可以证明:AB=AN=10,
∴BM=CN=4,
∵AD⊥CM,AM=AC,
∴DM=DC,同理BE=EN,
∵BF=CF,
∴FD=BM=2,EF=CN=2,
∵∠DFE=135°,
∴∠EFH=45°,EH=EF=,
∴S△DEF= DF HE=,
故答案为.
25.解:∵AD平分∠BAC,BD⊥AD,
∴AB=AE=6,BD=DE,
∴CE=AC﹣AE=10﹣6=4,
∵BD=DE,F为BC的中点,
∵△ABC的面积为30,
∴S△BCE=S△ABC=×30=12,
连接CD,
∴S△BCD=S△BCE=×12=3.
故答案为:3.
26.解:连接BD,取BD的中点H,连接EH、FH,
由题意可知:GE是线段AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
,
∴△AGD≌△BGC(SAS),
∴AD=BC,
∵点E、F、H分别是AB、CD、BD的中点,
∴EH∥AD,EH=AD,FH∥BC,FH=BC,
∵AD=BC,
∴EH=FH,
∵直线AD与直线BC垂直,
∴EH⊥FH,
∴=,
∴=,
故答案为:.
27.解:取BF的中点G,连接CG,如图所示:
∵C是BD的中点,
∴CG是△BDF的中位线,
∴CG∥DF,CG=DF,
∵E是AC的中点,
∴EF是△ACG的中位线,
∴EF=CG,
∴EF=DF,
即DF=4EF,
∴ED=3EF,
∴=,
故答案为:.
28.解:如图,取AB中点F,连接DF,作FG⊥DE于G.
∵点D为△ABC的边AC的中点,F为AB中点,
∴DF是△ABC的中位线,
∴DF∥BC,DF=BC,
∴∠EFD=∠ABC=120°,
∵∠AED=150°,
∴∠DEF=180°﹣∠AED=30°,
∠EDF=∠AED﹣EFD=30°,
∴∠DEF=∠EDF=30°,
∴DF=EF,
∵FG⊥DE,
∴DG=DE.
在Rt△DGF中,∵∠DGF=90°,∠GDF=30°,
∴GF=DF,DG=GF=DF,
∴===.
故答案为:.
29.解:∵DE是△ABC的中位线,
∴DE=BC,DE∥BC,
∵DF=FE,
∴DF=BC,
∴==,
∴=,
∵AD=BD,
∴GD:AD=1:3,
∴AG:GD=2:1,
故答案为2.
1.如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且=,作∠ACB的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为 .
2.如图,四边形ABCD中,点E、F分别为AD、BC的中点,延长FE交CD延长线于点G,交BA延长线于点H,若∠BHF与∠CGF互余,AB=4,CD=6,则EF的长为 .
3.如图,在△ABC中,E是AB的中点,D是AC上一点,连接DE,BH⊥AC于H,若2∠ADE=90°﹣∠HBC,AD:BC=4:3,CD=2,则BC的长为 .
4.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点,连接AF,BF,∠AFB=90°.已知AB=6,BC=10,则EF的长是 .
5.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=13,AC=8,则DF的长为 .
6.如图,在四边形ABCD中,AB∥CD,AD∥BC,点E为CD上一点且DE=3EC,点F,G分别是AE,BE的中点,若FG=4cm,则DE的长度为 .
7.如图所示,在四边形ABCD中,AB=CD=4,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=80°,则MN的长是 .
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为 .
9.如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF= .
10.如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC= .
11.如图,D,E,F分别是等边△ABC三边的中点,AB=4,则四边形DECF的周长为 .
12.如图已知,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,连接MN,如果AB=10,BC=15.MN=3,那么△ABC的周长是 .
13.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
14.如图,在△ABC中,E、F、G、H分别为AB、AC、DC、BD的中点,若AD=3,BC=8,则四边形EFGH的周长是 .
15.如图,在△ABC中,AB2﹣BC2=AC2,点D是边BC上一点,点E、F分别是AB、AD的中点.若AB=12,AD=10,EF=2,则△CEF的周长是 .
16.如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠BEF= 度.
17.如图,已知△ABC中,∠BAC=68°,点D、E、F分别是三角形三边AB,AC,BC的中点,AM是三角形BC边上的高,连接DM,EM,EF,则∠DME= °,∠DFE= °.
18.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
19.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,则∠ADC的度数为 .
20.已知,在四边形ABCD中,AB=CD,E是BC的中点,G是AD的中点,EG交AC于点F,∠ACD=30°,∠CAB=70°,则∠AFG的度数是 .
21.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
22.如图,△ABC中,若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF的面积为6,则△ABC的面积= .
23.如图,△ABC中,AB=AC,AD⊥BC于点D,点E在AC上,CE=2AE,AD=9,BE=10,AD与BE交于点F,则△ABC的面积是 .
24.如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连接DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是 .
25.如图,在△ABC中,AD平分∠BAC,BD⊥AD于点D,延长BD交AC于点E,点F为BC中点,连接DF.若AB=6,AC=10,△ABC的面积为30,则△BDF的面积为 .
26.如图,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.若AD、BC所在直线互相垂直,的值为 .
27.如图,已知E是AC的中点,C是BD的中点,那么= .
28.如图,点D为△ABC的边AC的中点,点E为AB上一点,若∠AED=150°,∠ABC=120°,则的值为 .
29.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD的值为 .
参考答案
1.解:∵DC=AC=10,∠ACB的平分线CF交AD于F,
∴F为AD的中点,CF⊥AD,
∴∠CFD=90°,
∵DC=10,CF=8,
∴DF==6,
∴AD=2DF=12,
∵=,
∴BD=8,
∵点E是AB的中点,
∴EF为△ABD的中位线,
∴EF=BD=4,
故答案为:4.
2.解:连接BD,取BD的中点M,连接EM,FM,
∵E、F分别为AD、BC的中点,M为BD的中点,
∴EM,MF分别为△ADB、△BCD的中位线,
∴EM∥AB,MF∥DC,EM=AB=2,MF=DC=3,
∵MF∥DC,
∴∠BFM=∠BCD,
∵∠FGC+∠GCF=∠BFH=∠BFM+∠EFM,
∴∠FGC=∠EFM,
∵EM∥AB,
∴∠FEM=∠FHB,
∵∠BHF与∠CGF互余,
∴∠CGF+∠BHF=∠EFM+∠FEM=90°,
∴∠EMF=180°﹣∠EFM﹣∠FEM=90°,
∴△EMF是直角三角形,
∴EF=,
故答案为:.
3.解:如图,延长AC至N,使CN=BC,连接BN,
∵2∠ADE=90°﹣∠HBC,∠BCA=90°﹣∠HBC,
∴∠BCA=2∠ADE,
∵CN=BC,
∴∠N=∠CBN,
∴∠BCA=∠N+∠CBN=2∠N,
∴∠ADE=∠N,
∴DE∥BN,
又∵E是AB的中点,
∴DE是△ABN的中位线,
∴AD=DN,
∵AD:BC=4:3,
∴设AD=DN=4x,BC=CN=3x,
∴CD=DN﹣CN=x=2,
∴BC=6,
故答案为6.
4.解:∵点D,E分别是边AB,AC的中点,BC=10,
∴DE=BC=5,
在Rt△AFB中,点D是边AB的中点,AB=6,
∴DF=AB=3,
∴EF=DE﹣DF=5﹣3=2,
故答案为:2.
5.解:延长CF交AB于点G,
∵AE平分∠BAC,
∴∠GAF=∠CAF,
∴AF垂直平分CG,
∴AC=AG,
GF=CF,
又∵点D是BC中点,
∴DF是△CBG的中位线,
∴DF=BG=(AB﹣AG)=(AB﹣AC)=2.5,
故答案为:2.5.
6.解:如图,在四边形ABCD中,AB∥CD,AD∥BC,则四边形ABCD是平行四边形,故AB=CD.
∵点F,G分别是AE,BE的中点,
∴FG是△AEB的中位线.
∴AB=2FG=8cm.
∴CD=AB=8cm.
∵DE=3EC,
∴DE=6cm.
故答案是:6cm.
7.解:作PH⊥MN于H,
∵M、N、P分别是AD、BC、BD的中点,
∴PM=AB=2,PN=CD=2,PM∥AB,PN∥CD,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=80°,PM=PN,
∴∠MPN=120°,
∵PM=PN,
∴∠PMN=30°,MH=HN,
∴PH=PM=1,
由勾股定理得,MH==,
∴MN=2MH=2,
故答案为:2.
8.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24厘米,
∴OA+OB=12cm,
∵△OAB的周长是18厘米,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3cm.
故答案为:3cm.
9.解:连接DE,
∵四边形ABCD为直角梯形,AB=AD=a,CD=,CB⊥AB,点E,F分别为线段AB,AD的中点
∴△AED为直角三角形.则EF是Rt△AED斜边上的中线,
由直角三角形斜边上的中线等于斜边的一半得,EF=DE=AB=.
故答案为:
10.解:取线段BC的中点E,连接EM、EN,如图所示.
∵M、N,E分别为AB,CD,BC的中点,
∴ME∥AC,ME=AC,NE∥BD,NE=BD=,
∴∠EMN=∠FQP,∠ENM=∠FPQ.
又∵∠FPQ=∠FQP,
∴∠EMN=∠ENM.
∴ME=NE=.
∴AC=2ME=9.
故答案为:9.
11.解:∵△ABC为等边三角形,AB=4,
∴AC=BC=AB=4,
∵D,E,F分别是等边△ABC三边的中点,
∴DF=BC=2,EC=BC=2,DE=AC=2,FC=AC=2,
∴四边形DECF的周长=2+2+2+2=8,
故答案为:8.
12.解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=10,BN=ND,
∵BM=MC,
∴DC=2MN=6,
∴AC=AD+DC=16,
∴△ABC的周长=AB+BC+AC=10+15+16=41,
故答案为:41.
13.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=3,
∴DE=2MN=6,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=22,
∴△ABC的周长=AB+AC+BC=22+16=38,
故答案为:38.
14.解:∵E、F分别为AB、AC的中点,
∴EF=BC=4,
同理可得,FG=AD=1.5,GH=BC=4,EH=AD=1.5,
∴四边形EFGH的周长=4+1.5+4+1.5=11,
故答案为:11.
15.解:∵AB2﹣BC2=AC2,
∴∠ACB=90°,
∵点E、F分别是AB、AD的中点,AB=12,AD=10,
∴CE=AB=6,CF=AD=5,
∵EF=2,
∴△CEF的周长=CE+CF+EF=13,
故答案为:13.
16.解:∵E是AB的中点,F是AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,
∴∠BEF=180°﹣∠B=180°﹣50°=130°,
故答案为:130.
17.解:∵∠BAC=68°,
∴∠B+∠C=180°﹣68°=112°,
∵AM是三角形BC边上的高,
∴∠AMB=∠AMC=90°,
在Rt△AMB中,D是AB的中点,
∴DM=AB=DB,
∴∠DMB=∠B,
同理可得,∠EMC=∠C,
∴∠DMB+∠EMC=∠B+∠C=112°,
∴∠DME=180°﹣(∠DMB+∠EMC)=68°,
∵点D、E、F分别是三角形三边AB,AC,BC的中点,
∴DF、EF分别是△ABC的中位线,
DF∥AC,EF∥AB,
∴∠DFB=∠C,∠EFC=∠B,
∴∠DFB+∠EFC=∠B+∠C=112°,
∴∠DFE=180°﹣(∠DFB+∠EFC)=68°,
故答案为:68;68.
18.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
19.解:连接BD,
∵E、F分别是边AB、AD的中点,
∴EF∥BD,BD=2EF=12,
∴∠ADB=∠AFE=50°,
BD2+CD2=225,BC2=225,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=140°,
故答案为:140°.
20.解:取AC的中点M,连接GM、EM,
∵G是AD的中点,E是BC 的中点,
∴GM是△ADC的中位线,EM是△ABC的中位线,
∴GM=DC,EM=,GM∥CD,EM∥AB,
∵AB=CD,
∴GM=EM,
∴∠GEM=∠EGM,
∵EM∥AB,
∴∠EMC=∠BAC=70°,
∴∠AME=180°﹣70°=110°,
∵GM∥CD,
∴∠AMG=∠ACD=30°,
∴∠EMG=110°+30°=140°,
∴∠EGM==20°,
∴∠AFG=∠EGM+∠AMG=20°+30°=50°,
故答案为50°.
21.解:∵D、E分别为AC、BC的中点,
即DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴AB=2DE,DF∥AB,
又∵BF∥AC,
∴BF∥AD,
∴四边形ABFD是平行四边形,
∵AB⊥BE,
∴S平行四边形ABFD=AB BE,
∵DE=2,
∴AB=2×2=4,
在Rt△ABC中,
∵∠C=30°,
∴AC=2AB=2×4=8,
∴BC===4,
∴BE=BC=2,
∴S平行四边形ABFD=4×2=8,
故答案为8.
22.解:∵点F是CD的中点,
∴S△DEF=S△CEF,
设S△DEF=S△CEF=x,
∵D、E分别是AB、AC的中点,
∴S△ADE=S△CDE=2x,S△BDC=S△ADC=4x,S△BDF=2x,
∴S 四边形BDEF=3x.
∵S 四边形BDEF=6,
∴3x=6,
∴x=2,
∴S△ABC=2S△BDC=8x=16,
故答案为:16.
23.解:如图,取CE的中点G,连接DG.
∵△ABC中,AB=AC,AD⊥BC,
∴BD=CD,即点D是BC的中点,
∴GD是△BCE的中位线,
∴DG∥BE,DG=BE=5.
又∵CE=2AE,
∴AE=GE,即点E是AG的中点,
∴点F是AD的中点,
∴AF=DF=4.5,EF是△ADG的中位线,
∴EF=DG=2.5,
∴BF=BE﹣EF=7.5.
则在直角△BFD中,由勾股定理易求BD=6.
∴BC=12.
则△ABC的面积是:BC AD=×12×9=54.
故答案是:54.
24.解:延长CD交AB于M,延长AC、BE交于点N,作EH⊥DF交DF的延长线于H.
∵AD⊥CM,
∴∠ADC=∠ADM=90°,
∵∠DAM=∠DAC,∠DAM+∠AMC=90°,∠DAC+∠ACM=90°,
∴∠AMC=∠ACM,
∴AM=AC=6,同理可以证明:AB=AN=10,
∴BM=CN=4,
∵AD⊥CM,AM=AC,
∴DM=DC,同理BE=EN,
∵BF=CF,
∴FD=BM=2,EF=CN=2,
∵∠DFE=135°,
∴∠EFH=45°,EH=EF=,
∴S△DEF= DF HE=,
故答案为.
25.解:∵AD平分∠BAC,BD⊥AD,
∴AB=AE=6,BD=DE,
∴CE=AC﹣AE=10﹣6=4,
∵BD=DE,F为BC的中点,
∵△ABC的面积为30,
∴S△BCE=S△ABC=×30=12,
连接CD,
∴S△BCD=S△BCE=×12=3.
故答案为:3.
26.解:连接BD,取BD的中点H,连接EH、FH,
由题意可知:GE是线段AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
,
∴△AGD≌△BGC(SAS),
∴AD=BC,
∵点E、F、H分别是AB、CD、BD的中点,
∴EH∥AD,EH=AD,FH∥BC,FH=BC,
∵AD=BC,
∴EH=FH,
∵直线AD与直线BC垂直,
∴EH⊥FH,
∴=,
∴=,
故答案为:.
27.解:取BF的中点G,连接CG,如图所示:
∵C是BD的中点,
∴CG是△BDF的中位线,
∴CG∥DF,CG=DF,
∵E是AC的中点,
∴EF是△ACG的中位线,
∴EF=CG,
∴EF=DF,
即DF=4EF,
∴ED=3EF,
∴=,
故答案为:.
28.解:如图,取AB中点F,连接DF,作FG⊥DE于G.
∵点D为△ABC的边AC的中点,F为AB中点,
∴DF是△ABC的中位线,
∴DF∥BC,DF=BC,
∴∠EFD=∠ABC=120°,
∵∠AED=150°,
∴∠DEF=180°﹣∠AED=30°,
∠EDF=∠AED﹣EFD=30°,
∴∠DEF=∠EDF=30°,
∴DF=EF,
∵FG⊥DE,
∴DG=DE.
在Rt△DGF中,∵∠DGF=90°,∠GDF=30°,
∴GF=DF,DG=GF=DF,
∴===.
故答案为:.
29.解:∵DE是△ABC的中位线,
∴DE=BC,DE∥BC,
∵DF=FE,
∴DF=BC,
∴==,
∴=,
∵AD=BD,
∴GD:AD=1:3,
∴AG:GD=2:1,
故答案为2.
