勾股定理(一)课件
图片预览


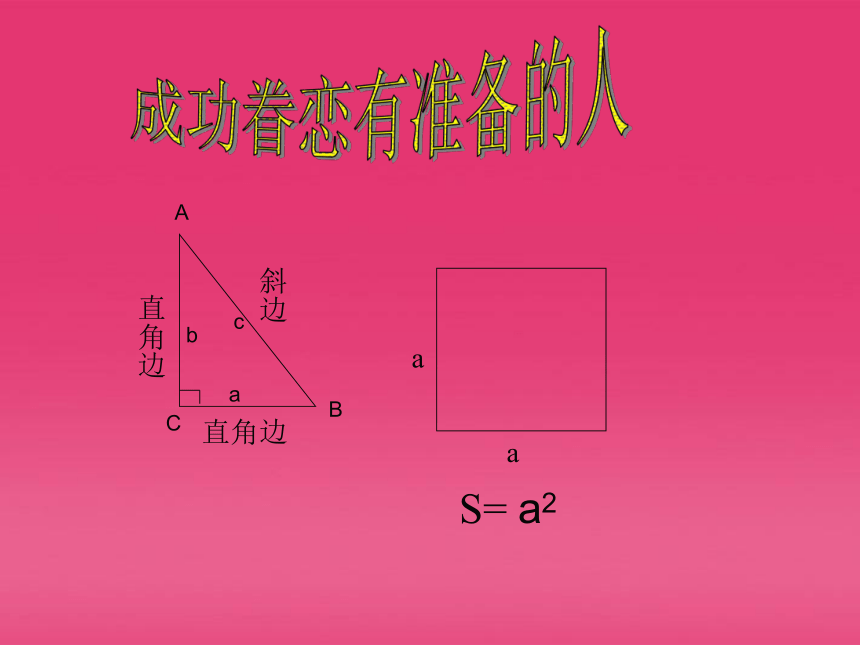


文档简介
(共26张PPT)
八年级(上)第十四章
勾股定理
人类一直想弄清楚其他星球上是否存在着“人”,并试图与“他们”取得联系,那么我们怎样才能与“外星人”接触呢?数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号。
勾股定理有着悠久的历史。古巴比伦人和古代中国人看出了这个关系;古希腊的毕达哥拉斯学派首先证明了这个关系,很多具有古老文化的民族和国家都会说:我们首先认识的数学定理是勾股定理。
直角边
直角边
斜边
a
a
S= a2
A
B
C
c
a
b
如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?
9米
12米
提出问题
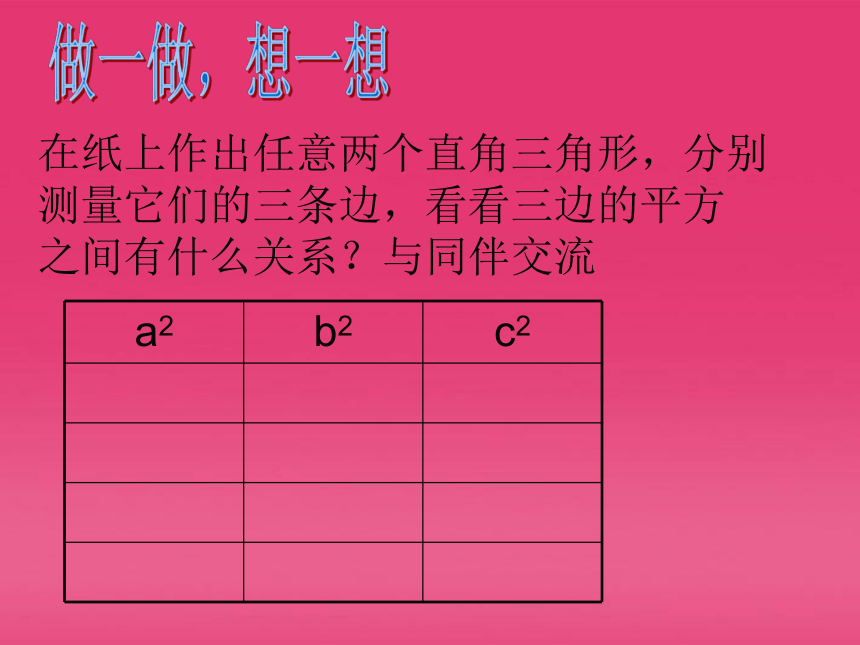
在纸上作出任意两个直角三角形,分别
测量它们的三条边,看看三边的平方
之间有什么关系?与同伴交流
a2 b2 c2
探索1
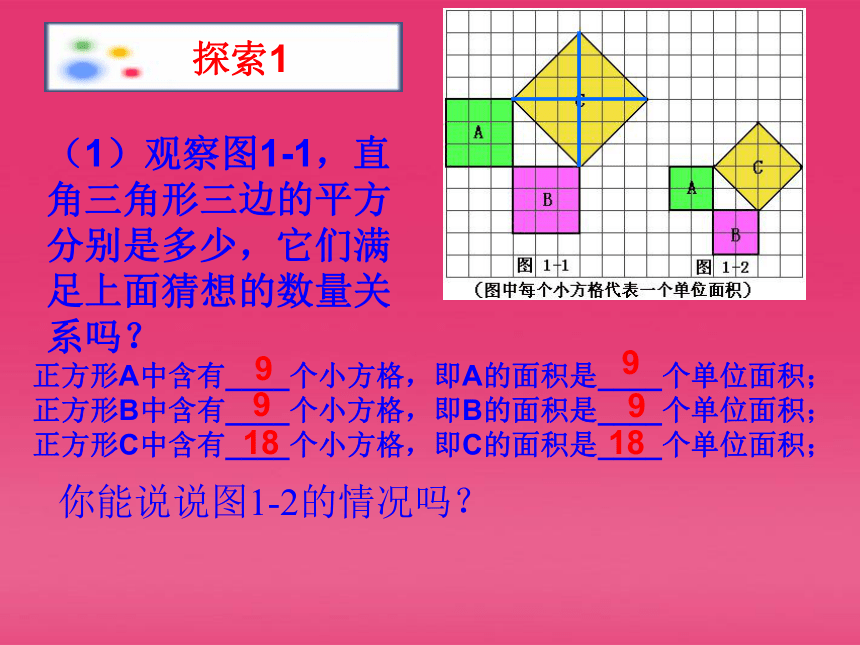
(1)观察图1-1,直角三角形三边的平方分别是多少,它们满足上面猜想的数量关系吗?
正方形A中含有____个小方格,即A的面积是____个单位面积;
正方形B中含有____个小方格,即B的面积是____个单位面积;
正方形C中含有____个小方格,即C的面积是____个单位面积;
9
9
18
18
9
9
你能说说图1-2的情况吗?
做一做
A的面积
(单位面积) B的面积
(单位面积) C的面积
(单位面积)
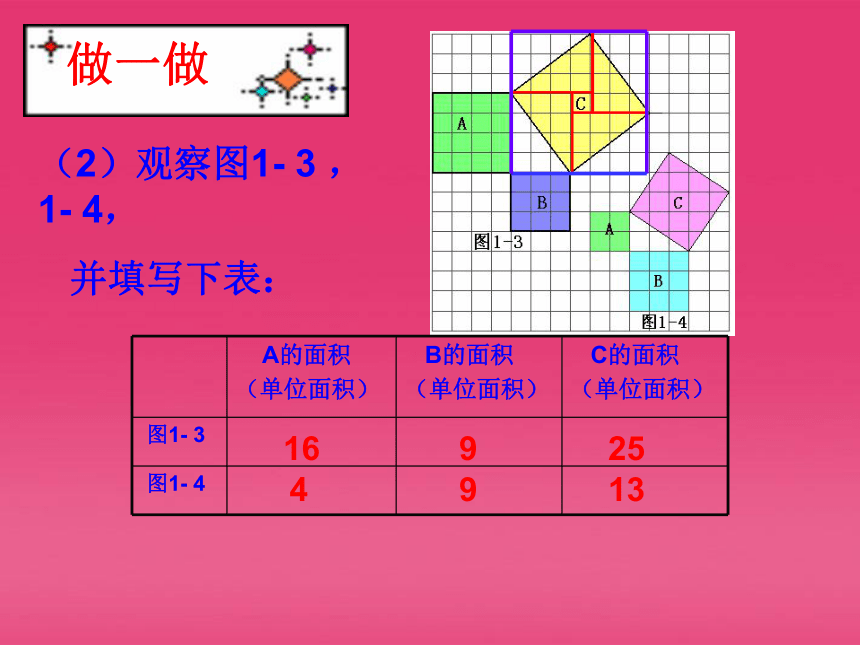
图1- 3
图1- 4
16
9
25
4
9
13
(2)观察图1- 3 ,1- 4,
并填写下表:
以直角边为边长的两个正方形的面积和等于以斜边为边长的正方形的面积
D
C
B
A
8
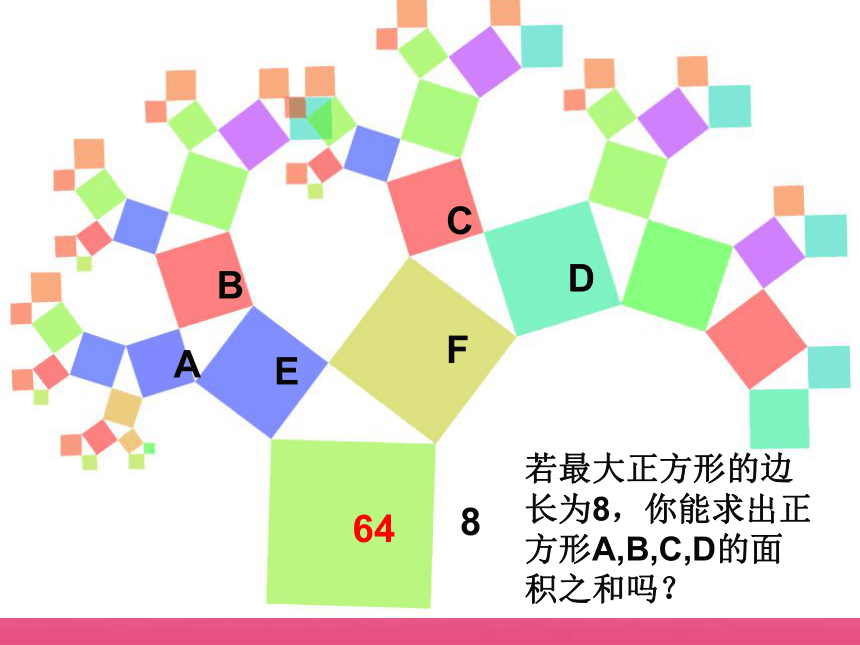
若最大正方形的边长为8,你能求出正方形A,B,C,D的面积之和吗?
F
E
64
a
b
c
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
弦图
现在我们一起来探索“弦图”的奥妙吧!
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称弦。
勾
股
弦
勾股定理(毕达哥拉斯定理)
直角三角形两直角边的平方和等于斜边的平方,如果用a、b和c分别表示直角三角形的两直角边和斜边,那么 a2+ b2= c2
a
b
c
∵ △ABC为直角三角形,
∴ AC2+BC2=AB2.
(或a2+b2=c2)
A
C
B
几何语言表述
判断
直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a +b =c .
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
例1 已知Rt△ABC中,∠C=90°.
①若a = 5,b =12 ,求c 的长。
②若c= 10,b = 8, 求a 的长。
例2 若一个直角三角形的三边长分别为3,
4, x,求x的值。
A
B
C
定理应用
判断:直角三角形的两边长分别是3和4,则第三边长是5. ( )
例3 如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?
9米
12米
定理应用
勇闯新高
如图,一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处。折断处离地面的高度是多少?
练一练
1、求下图中字母所代表的正方形的面积。
225
400
A
81
225
B
625
144
2、求出下列直角三角形中未知边的长度。
6
8
x
5
x
13
10
12
3、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
4判断
■在直角三角形中,两边的平方和等于第三边的平方. ( )
■若三角形的三边长a、b、c满足
(a+b)2=c2+2ab.那么这个三角形是直角三角形 ( )
■若a、b、c为Rt△ABC的三边,且∠C=90°,则a2+b2=c2. ( )
√
×
√
◆若a=6,c=10,则b=____.
在Rt△ABC中,∠C=900.
◆若a=12,b=5,则斜边c上的高h=___.
◆若a:b=3:4,c=10,则a=___,b=___.
8
8
6
5填空
◆若直角三角形的三边为6、8、x,则x的长为 ( )
A.6 B.8
C.10 D.以上答案均不对
D
6选择
7 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是7cm,则正方形A、B、C、D的面积之和是______.
49cm2
7cm
A
B
C
D
小结:
1、通过用格点三角形及“弦图”的方式探索直角三角形两直角边与斜边之间的关系。
2、得到直角三角形两直角边与斜边之间的关系——勾股定理:直角三角形两直角边的平方和等于斜边的平方。
3、练习的使用了勾股定理来解决直角三角形里的一些问题。
这些内容你都掌握清楚了吗?
谢谢
八年级(上)第十四章
勾股定理
人类一直想弄清楚其他星球上是否存在着“人”,并试图与“他们”取得联系,那么我们怎样才能与“外星人”接触呢?数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号。
勾股定理有着悠久的历史。古巴比伦人和古代中国人看出了这个关系;古希腊的毕达哥拉斯学派首先证明了这个关系,很多具有古老文化的民族和国家都会说:我们首先认识的数学定理是勾股定理。
直角边
直角边
斜边
a
a
S= a2
A
B
C
c
a
b
如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?
9米
12米
提出问题
在纸上作出任意两个直角三角形,分别
测量它们的三条边,看看三边的平方
之间有什么关系?与同伴交流
a2 b2 c2
探索1
(1)观察图1-1,直角三角形三边的平方分别是多少,它们满足上面猜想的数量关系吗?
正方形A中含有____个小方格,即A的面积是____个单位面积;
正方形B中含有____个小方格,即B的面积是____个单位面积;
正方形C中含有____个小方格,即C的面积是____个单位面积;
9
9
18
18
9
9
你能说说图1-2的情况吗?
做一做
A的面积
(单位面积) B的面积
(单位面积) C的面积
(单位面积)
图1- 3
图1- 4
16
9
25
4
9
13
(2)观察图1- 3 ,1- 4,
并填写下表:
以直角边为边长的两个正方形的面积和等于以斜边为边长的正方形的面积
D
C
B
A
8
若最大正方形的边长为8,你能求出正方形A,B,C,D的面积之和吗?
F
E
64
a
b
c
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
弦图
现在我们一起来探索“弦图”的奥妙吧!
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称弦。
勾
股
弦
勾股定理(毕达哥拉斯定理)
直角三角形两直角边的平方和等于斜边的平方,如果用a、b和c分别表示直角三角形的两直角边和斜边,那么 a2+ b2= c2
a
b
c
∵ △ABC为直角三角形,
∴ AC2+BC2=AB2.
(或a2+b2=c2)
A
C
B
几何语言表述
判断
直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a +b =c .
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
例1 已知Rt△ABC中,∠C=90°.
①若a = 5,b =12 ,求c 的长。
②若c= 10,b = 8, 求a 的长。
例2 若一个直角三角形的三边长分别为3,
4, x,求x的值。
A
B
C
定理应用
判断:直角三角形的两边长分别是3和4,则第三边长是5. ( )
例3 如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?
9米
12米
定理应用
勇闯新高
如图,一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处。折断处离地面的高度是多少?
练一练
1、求下图中字母所代表的正方形的面积。
225
400
A
81
225
B
625
144
2、求出下列直角三角形中未知边的长度。
6
8
x
5
x
13
10
12
3、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
4判断
■在直角三角形中,两边的平方和等于第三边的平方. ( )
■若三角形的三边长a、b、c满足
(a+b)2=c2+2ab.那么这个三角形是直角三角形 ( )
■若a、b、c为Rt△ABC的三边,且∠C=90°,则a2+b2=c2. ( )
√
×
√
◆若a=6,c=10,则b=____.
在Rt△ABC中,∠C=900.
◆若a=12,b=5,则斜边c上的高h=___.
◆若a:b=3:4,c=10,则a=___,b=___.
8
8
6
5填空
◆若直角三角形的三边为6、8、x,则x的长为 ( )
A.6 B.8
C.10 D.以上答案均不对
D
6选择
7 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是7cm,则正方形A、B、C、D的面积之和是______.
49cm2
7cm
A
B
C
D
小结:
1、通过用格点三角形及“弦图”的方式探索直角三角形两直角边与斜边之间的关系。
2、得到直角三角形两直角边与斜边之间的关系——勾股定理:直角三角形两直角边的平方和等于斜边的平方。
3、练习的使用了勾股定理来解决直角三角形里的一些问题。
这些内容你都掌握清楚了吗?
谢谢
