2021-2022学年华东师大版八年级数学上册《第14章勾股定理》同步达标训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册《第14章勾股定理》同步达标训练 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 398.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 23:37:40 | ||
图片预览


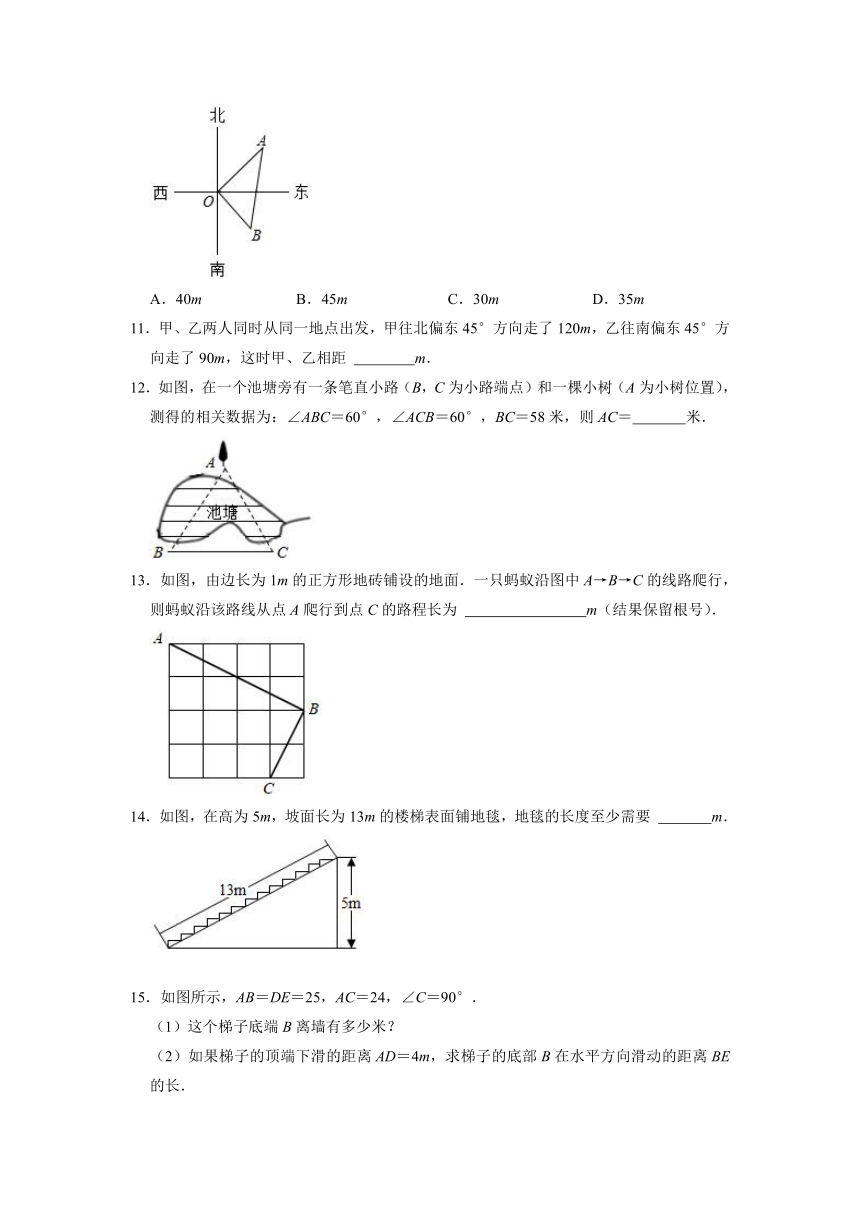


文档简介
2021-2022学年华师大版八年级数学上册《第14章勾股定理》同步达标训练(附答案)
1.如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,则蝴蛛所走的最短路线的长度是( )
A.20cm B.25cm C.23cm D.24cm
2.为了预防新冠疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地AB=2.1米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,则人头顶离测温仪的距离AD等于( )
A.1.2米 B.1.3米 C.1.4米 D.1.5米
3.国庆节期间,重庆南开中学用彩灯带装饰了艺术楼大厅的所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为( )
A.米 B.米 C.米 D.5米
4.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km B.14km C.11km D.10km
5.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
6.如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为( )
A.5尺 B.25尺 C.13尺 D.12尺
7.我国古代著名的“赵爽弦图”的示意图如图所示,它是由四个全等的直角三角形围成的.若AC=2,BC=3,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到一个如图所示“数学风车”,则这个风车的外围周长是( )
A. B.8 C. D.
8.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露出在杯子外面长为hcm,则h的取值范围是( )
A.0≤h≤12 B.12≤h≤13 C.11≤h≤12 D.12≤h≤24
9.如图,正四棱柱的底面边长为10cm,侧棱长为16cm,一只蚂蚁从点A出发,沿棱柱侧面到点C′处吃食物,那么它需要爬行的最短路径的长是( )cm.
A.8 B.4 C.2 D.12
10.如图,在水塔O的东北方向24m处有一抽水站A,在水塔的东南方向18m处有一建筑工地B,在AB间建一条直水管,则水管AB的长为( )
A.40m B.45m C.30m D.35m
11.甲、乙两人同时从同一地点出发,甲往北偏东45°方向走了120m,乙往南偏东45°方向走了90m,这时甲、乙相距 m.
12.如图,在一个池塘旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置),测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=58米,则AC= 米.
13.如图,由边长为1m的正方形地砖铺设的地面.一只蚂蚁沿图中A→B→C的线路爬行,则蚂蚁沿该路线从点A爬行到点C的路程长为 m(结果保留根号).
14.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 m.
15.如图所示,AB=DE=25,AC=24,∠C=90°.
(1)这个梯子底端B离墙有多少米?
(2)如果梯子的顶端下滑的距离AD=4m,求梯子的底部B在水平方向滑动的距离BE的长.
16.为了丰富少年儿童的业余生活,某社区要在如图所示的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=5千米,CA=3千米,DB=2千米,试问:
(1)图书室E应该建在距点A多少千米处,即AE= 千米,才能使它到两所学校的距离相等?
(2)证明上题中的结论.
17.勾股定理是一个基本的几何定理,早在我国西汉时期的《周髀算经》就有“勾三股四弦五”的记载.如果一个三角形三边长都是正整数,这三个正整数叫做一组“勾股数”,如:3,4,5;5,12,13;等都是勾股数.把勾股数同时乘以相同的正整数倍得到的也是勾股数,我们把这种勾股数称为“派生勾股数”.因为6=3×2,8=4×2,10=5×2,那么6,8,10就是“派生勾股数”,如果一组勾股数斜边比一条直角边大3,我们把这种勾股数称为“新新勾股数”.
(1)请判断9,12,16和10,24,26是否为“派生勾股数”;
(2)请求出斜边小于200的所有“新新勾股数”.
18.在数的发展中,我们发现有理数已经不能满足人们的需要,比如正方形ABCD的面积为2,则它的边长就不是一个有理数,所以就产生了像这样的无理数.
问题:
(1)如图1,在数轴上作出表示的点A(保留作图痕迹);
(2)如图2,在边长均为1的正方形网格中,画出线段AB(A、B均为格点),使得AB长为;
(3)已知Rt△ABC的面积为5,点A、B、C均为格点,点A如图所示.请在图3网格中画出Rt△ABC.
19.如图所示,△OA1A2、△OA2A3、△OA3A4、△OA4A5、…都是直角三角形,请细心观察图形,认真分析各式,然后解答问题.
OA22=()2+1=2,S1=;
OA32=12+()2=3,S2=;
OA42=12+()2=4,S3=;
…
(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S33+…+S102的值.
20.如图是由边长为1的小正方形拼成的网格.
(1)在图1网格中找格点P,使得AP与AB垂直.
(2)在图2网格中找格点P,使得△ABP的面积是3.
(3)在图3网格中找格点P,使得PA=PB.
21.如图,在△ABC中,∠A=60°,AB=4cm,AC=12cm.动点P从点A开始沿AB边以1cm/s的速度运动,动点Q从点C开始沿CA边以3cm/s的速度运动.点P和点Q同时出发,当点P到达点B时,点Q也随之停止运动.设动点的运动时间为ts(0<t<4),解答下列问题:
(1)当t为何值时,点A在PQ的垂直平分线上?
(2)在运动过程中,是否存在某一时刻t,使△APQ是直角三角形?若存在,求出t的值;若不存在,请说明理由.
22.教材中的探究:如图,把两个边长为1的小正方形沿对角线剪开,用所得到的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法(数轴的单位长度为1).
阅读理解:
图1中大正方形的边长为 ,图2中点A表示的数为 ;
迁移应用:
(2)请你参照上面的方法,把5个小正方形按图3位置摆放,并将其进行裁剪,拼成一个大正方形.
①请在图3中画出裁剪线,并在图3中画出所拼得的大正方形的示意图(画出一种即可).
②利用①中的成果,在图4的数轴上分别标出表示数﹣与2﹣的点,并比较它们的大小.
23.如图,每个小正方形的边长都为为1.
(1)求四边形ABCD的面积;
(2)证明:∠ABC=90°.
24.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)勾股定理的证明,人们已经找到了400多种方法,请从图1、图2中任选一种方法来证明该定理.(图1、图2均满足证明勾股定理所需的条件)
(2)如图3、图4、图5,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3有 个.(不需要证明)
25.如图,线段AB,BC,CD和BD都为5cm,动点P从点A出发沿A→B→D以2cm/s的速度运动到点D,动点Q从点D出发沿D→C→B→A以2.8cm/s的速度运动到点A.若两点同时开始运动5s时,P,Q相距3cm.试确定两点运动5s时,问△APQ的形状.
参考答案
1.解:如图所示,作点F关于直线AB的对称点F′,
则SF′长度即为蝴蛛所走的最短路线的长度,
∴SF'==25(cm).
即蝴蛛所走的最短路线的长度是25cn,
故选:B.
2.解:如图,过点D作DE⊥AB于点E,
∵AB=2.1米,BE=CD=1.6米,ED=BC=1.2米,
∴AE=AB﹣BE=2.1﹣1.6=0.5(米).
在Rt△ADE中,由勾股定理得到:AD===1.3(米),
故选:B.
3.解:将圆柱表面切开展开呈长方形,
则彩灯带长为2个长方形的对角线长,
∵圆柱高3米,底面周长2米,
∴AC2=22+1.52=6.25,
∴AC=2.5(米),
∴每根柱子所用彩灯带的最短长度为5m.
故选:D.
4.解:过点B作BC⊥AC,垂足为C.
观察图形可知AC=AF﹣MF+MC=8﹣3+1=6(km),BC=2+5=7(km),
在Rt△ACB中,AB===10(km).
答:登陆点到宝藏埋藏点的直线距离是10km,
故选:D.
5.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
6.解:如图:由题意可知AB=5尺,设AC长为x尺,则BC长为(25﹣x)尺,
在Rt△ABC中,由勾股定理得:AC2+AB2=BC2,
则x2+52=(25﹣x)2,
解得:x=12,即AC=12尺,
故选:D.
7.解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,
则x2=62+22=40,
所以x=2,
所以风车的外围周长为4(BD+AC)=4×(2+3)=8+12.
故选:D.
8.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:此时,AB===13(cm),
故h=24﹣13=11(cm).
故h的取值范围是:11cm≤h≤12cm.
故选:C.
9.解:把长方体展开为平面图形,分两种情形:
如图1中,AC′==2(cm),
如图2中,AC′==4(cm),
∵4<2,
∴爬行的最短路径是4cm,
故选:B.
10.解:∵OA是东北方向,OB是东南方向,
∴∠AOB=90°,
又∵OA=24m,OB=18m,
∴AB=
=
=30(m).
故选:C.
11.解:如图所示:由题意可得,∠AOB=90°,AO=120m,BO=90m,
则AB==150(m).
故答案为:150.
12.解:∵∠ABC=60°,∠ACB=60°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∵BC=58米,
∴AC=58米.
故答案为:58.
13.解:由勾股定理得:
AB=,BC=(m),
∴AB+BC=(m),
故答案为:3.
14.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
∴地毯的长度至少是12+5=17(米).
故答案为:17.
15.解:(1)由题意知AB=DE=25米,AC=24米,AD=4米,
在直角△ABC中,∠C=90°,
∴BC2+AC2=AB2,
∴米,
∴这个梯子底端离墙有7米;
(2)已知AD=4米,则CD=24﹣4=20(米),
在直角△CDE中,∠C=90°,
∴BD2+CE2=DE2,
∴(米),
∴BE=15﹣7=8(米),
答:梯子的底部在水平方向滑动了8m.
16.(1)解:设AE=x千米,则EB=(5﹣x)千米,
∵CA⊥AB,DB⊥AB,
∴∠CAE=∠EBD=90°,
在Rt△ACE和Rt△EBD中,由勾股定理得:AC2+AE2=EC2,BE2+DB2=ED2,
由题意得:EC=ED,
∴CA2+AE2=BE2+DB2,
∴32+x2=(5﹣x)2+22,
解得:x=2,
即AE=2千米,
故答案为:2;
(2)证明:由(1)得:AE=2千米,EB=3千米,
∵CA=3千米,DB=2千米,
∴CA=EB,AE=DB,
在△ACE和△BED中,
,
∴△ACE≌△BED(SAS),
∴EC=ED.
17.解:(1)∵9=3×3,12=4×3,16÷3≠5,
∴9,12,16不是“派生勾股数”;
∵10=5×2,24=12×2,26=13×2,
∴10,24,26是“派生勾股数”;
(2)勾股数3,4,5,把勾股数同时乘以3可得9,12,15,15﹣12=3,9,12,15是“新新勾股数”;
勾股数5,12,13,把勾股数同时乘以3可得15,36,39,39﹣36=3,15,36,39是“新新勾股数”;
勾股数7,24,25,把勾股数同时乘以3可得21,72,75,75﹣72=3,21,72,75是“新新勾股数”;
勾股数9,40,41,把勾股数同时乘以3可得27,120,123,123﹣120=3,27,120,123是“新新勾股数”;
勾股数11,60,61,把勾股数同时乘以3可得33,180,183,183﹣180=3,33,180,183是“新新勾股数”.
综上所述,斜边小于200的所有“新新勾股数”有9,12,15;15,36,39;21,72,75;27,120,123;33,180,183.
18.解:(1)如图所示:点E即为所求;
(2)如图所示:AB=;
(3)如图所示,△ABC即为所求.
19.解:(1)结合已知数据,可得:
OAn2=n,则Sn=;
(2)∵OAn2=n,
∴OA10=;
(3)S12+S22+S32+…+S102
=++++…+
=
=.
20.解:(1)如图1,AP⊥AB.
(2)如图2,△ABP的面积==3.
∴格点P使得△ABP的面积是3(答案不唯一).
(3)如图3,∵PA==,PB==,
∴格点P使得PA=PB(答案不唯一).
21.解:(1)若点A在线段PQ的垂直平分线上,则AP=AQ,
∵AP=t,AQ=12﹣3t,
∴t=12﹣3t,
解得:t=3,
答:当t=3时,点A在线段PQ的垂直平分线上;
(2)①若∠APQ=90°,
则△APQ是直角三角形,
∵∠A=60°,
∴∠AQP=30°,
∴AQ=2AP,
∴12﹣3t=2t,
∴t=,
②若∠AQP=90°,
则△APQ是直角三角形,
∵∠A=60°,
∴∠APQ=30°,
∴AP=2AQ,
∴t=2(12﹣3t),
∴t=.
∴当t=或时,△APQ是直角三角形.
22.解:(1)由图可得,点A到原点的距离为:,点A在原点右侧,
∴点A表示的实数为,
故答案为:,;
(2)①如图所示:
②表示数﹣与2﹣的点如图所示:
∴﹣<2﹣.
解:(1)由题意得四边形ABCD的面积为:
;
(2)证明:如图,连接AC,
∵AB2=32+22=13,BC2=32+22=13,AC2=52+12=26,且13+13=26,
∴AB2+BC2=AC2.
∴∠ABC=90°.
24.解:(1)如选择图1,四个相同的直角三角形的面积和再加上中间小四边形的面积等于大正方形的面积,
即
化简得:a2+b2=c2,
如选择图2,大正方形的面积等于四个相同的直角三角形的面积和再加上中间四边形的面积,
即,
化简得:a2+b2=c2.
(2)在图3中,
∵在直角三角形中,两条直角边的平方和等于斜边的平方,
即:a2+b2=c2.
∴S1+S2=a2+b2,S3=c2,
∴S1+S2=S3,
在图4中,
∵S1=π=,
S2==,
S3==,
∵a2+b2=c2,
∴S1+S2=S3,
在图5中,
∵S1=a×a=a2,
S2=b×b=,
S3=c×c=,
而a2+b2=c2,
∴S1+S2=S3,
∴三个图形中面积关系满足S1+S2=S3的有3个,
故答案为:3.
25.解:5s时,动点P运动的路程为2×5=10(cm),即点P运动到D点(点P与点D重合),
动点Q运动的路程为2.8×5=14(cm),
因为DC=BC=BA=5cm,
所以点Q在BA上,且BQ=14﹣10=4(cm).
在△BPQ中,因为BP=5cm,BQ=4cm,PQ=3cm,
所以BQ2+PQ2=42+32=25=BP2,
所以△BPQ是直角三角形,且∠BQP=90°,
所以∠AQP=180°﹣90°=90°,
所以两点运动5s时,△APQ是直角三角形.
1.如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,则蝴蛛所走的最短路线的长度是( )
A.20cm B.25cm C.23cm D.24cm
2.为了预防新冠疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地AB=2.1米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,则人头顶离测温仪的距离AD等于( )
A.1.2米 B.1.3米 C.1.4米 D.1.5米
3.国庆节期间,重庆南开中学用彩灯带装饰了艺术楼大厅的所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为( )
A.米 B.米 C.米 D.5米
4.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km B.14km C.11km D.10km
5.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
6.如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为( )
A.5尺 B.25尺 C.13尺 D.12尺
7.我国古代著名的“赵爽弦图”的示意图如图所示,它是由四个全等的直角三角形围成的.若AC=2,BC=3,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到一个如图所示“数学风车”,则这个风车的外围周长是( )
A. B.8 C. D.
8.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露出在杯子外面长为hcm,则h的取值范围是( )
A.0≤h≤12 B.12≤h≤13 C.11≤h≤12 D.12≤h≤24
9.如图,正四棱柱的底面边长为10cm,侧棱长为16cm,一只蚂蚁从点A出发,沿棱柱侧面到点C′处吃食物,那么它需要爬行的最短路径的长是( )cm.
A.8 B.4 C.2 D.12
10.如图,在水塔O的东北方向24m处有一抽水站A,在水塔的东南方向18m处有一建筑工地B,在AB间建一条直水管,则水管AB的长为( )
A.40m B.45m C.30m D.35m
11.甲、乙两人同时从同一地点出发,甲往北偏东45°方向走了120m,乙往南偏东45°方向走了90m,这时甲、乙相距 m.
12.如图,在一个池塘旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置),测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=58米,则AC= 米.
13.如图,由边长为1m的正方形地砖铺设的地面.一只蚂蚁沿图中A→B→C的线路爬行,则蚂蚁沿该路线从点A爬行到点C的路程长为 m(结果保留根号).
14.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 m.
15.如图所示,AB=DE=25,AC=24,∠C=90°.
(1)这个梯子底端B离墙有多少米?
(2)如果梯子的顶端下滑的距离AD=4m,求梯子的底部B在水平方向滑动的距离BE的长.
16.为了丰富少年儿童的业余生活,某社区要在如图所示的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=5千米,CA=3千米,DB=2千米,试问:
(1)图书室E应该建在距点A多少千米处,即AE= 千米,才能使它到两所学校的距离相等?
(2)证明上题中的结论.
17.勾股定理是一个基本的几何定理,早在我国西汉时期的《周髀算经》就有“勾三股四弦五”的记载.如果一个三角形三边长都是正整数,这三个正整数叫做一组“勾股数”,如:3,4,5;5,12,13;等都是勾股数.把勾股数同时乘以相同的正整数倍得到的也是勾股数,我们把这种勾股数称为“派生勾股数”.因为6=3×2,8=4×2,10=5×2,那么6,8,10就是“派生勾股数”,如果一组勾股数斜边比一条直角边大3,我们把这种勾股数称为“新新勾股数”.
(1)请判断9,12,16和10,24,26是否为“派生勾股数”;
(2)请求出斜边小于200的所有“新新勾股数”.
18.在数的发展中,我们发现有理数已经不能满足人们的需要,比如正方形ABCD的面积为2,则它的边长就不是一个有理数,所以就产生了像这样的无理数.
问题:
(1)如图1,在数轴上作出表示的点A(保留作图痕迹);
(2)如图2,在边长均为1的正方形网格中,画出线段AB(A、B均为格点),使得AB长为;
(3)已知Rt△ABC的面积为5,点A、B、C均为格点,点A如图所示.请在图3网格中画出Rt△ABC.
19.如图所示,△OA1A2、△OA2A3、△OA3A4、△OA4A5、…都是直角三角形,请细心观察图形,认真分析各式,然后解答问题.
OA22=()2+1=2,S1=;
OA32=12+()2=3,S2=;
OA42=12+()2=4,S3=;
…
(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S33+…+S102的值.
20.如图是由边长为1的小正方形拼成的网格.
(1)在图1网格中找格点P,使得AP与AB垂直.
(2)在图2网格中找格点P,使得△ABP的面积是3.
(3)在图3网格中找格点P,使得PA=PB.
21.如图,在△ABC中,∠A=60°,AB=4cm,AC=12cm.动点P从点A开始沿AB边以1cm/s的速度运动,动点Q从点C开始沿CA边以3cm/s的速度运动.点P和点Q同时出发,当点P到达点B时,点Q也随之停止运动.设动点的运动时间为ts(0<t<4),解答下列问题:
(1)当t为何值时,点A在PQ的垂直平分线上?
(2)在运动过程中,是否存在某一时刻t,使△APQ是直角三角形?若存在,求出t的值;若不存在,请说明理由.
22.教材中的探究:如图,把两个边长为1的小正方形沿对角线剪开,用所得到的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法(数轴的单位长度为1).
阅读理解:
图1中大正方形的边长为 ,图2中点A表示的数为 ;
迁移应用:
(2)请你参照上面的方法,把5个小正方形按图3位置摆放,并将其进行裁剪,拼成一个大正方形.
①请在图3中画出裁剪线,并在图3中画出所拼得的大正方形的示意图(画出一种即可).
②利用①中的成果,在图4的数轴上分别标出表示数﹣与2﹣的点,并比较它们的大小.
23.如图,每个小正方形的边长都为为1.
(1)求四边形ABCD的面积;
(2)证明:∠ABC=90°.
24.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)勾股定理的证明,人们已经找到了400多种方法,请从图1、图2中任选一种方法来证明该定理.(图1、图2均满足证明勾股定理所需的条件)
(2)如图3、图4、图5,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3有 个.(不需要证明)
25.如图,线段AB,BC,CD和BD都为5cm,动点P从点A出发沿A→B→D以2cm/s的速度运动到点D,动点Q从点D出发沿D→C→B→A以2.8cm/s的速度运动到点A.若两点同时开始运动5s时,P,Q相距3cm.试确定两点运动5s时,问△APQ的形状.
参考答案
1.解:如图所示,作点F关于直线AB的对称点F′,
则SF′长度即为蝴蛛所走的最短路线的长度,
∴SF'==25(cm).
即蝴蛛所走的最短路线的长度是25cn,
故选:B.
2.解:如图,过点D作DE⊥AB于点E,
∵AB=2.1米,BE=CD=1.6米,ED=BC=1.2米,
∴AE=AB﹣BE=2.1﹣1.6=0.5(米).
在Rt△ADE中,由勾股定理得到:AD===1.3(米),
故选:B.
3.解:将圆柱表面切开展开呈长方形,
则彩灯带长为2个长方形的对角线长,
∵圆柱高3米,底面周长2米,
∴AC2=22+1.52=6.25,
∴AC=2.5(米),
∴每根柱子所用彩灯带的最短长度为5m.
故选:D.
4.解:过点B作BC⊥AC,垂足为C.
观察图形可知AC=AF﹣MF+MC=8﹣3+1=6(km),BC=2+5=7(km),
在Rt△ACB中,AB===10(km).
答:登陆点到宝藏埋藏点的直线距离是10km,
故选:D.
5.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
6.解:如图:由题意可知AB=5尺,设AC长为x尺,则BC长为(25﹣x)尺,
在Rt△ABC中,由勾股定理得:AC2+AB2=BC2,
则x2+52=(25﹣x)2,
解得:x=12,即AC=12尺,
故选:D.
7.解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,
则x2=62+22=40,
所以x=2,
所以风车的外围周长为4(BD+AC)=4×(2+3)=8+12.
故选:D.
8.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:此时,AB===13(cm),
故h=24﹣13=11(cm).
故h的取值范围是:11cm≤h≤12cm.
故选:C.
9.解:把长方体展开为平面图形,分两种情形:
如图1中,AC′==2(cm),
如图2中,AC′==4(cm),
∵4<2,
∴爬行的最短路径是4cm,
故选:B.
10.解:∵OA是东北方向,OB是东南方向,
∴∠AOB=90°,
又∵OA=24m,OB=18m,
∴AB=
=
=30(m).
故选:C.
11.解:如图所示:由题意可得,∠AOB=90°,AO=120m,BO=90m,
则AB==150(m).
故答案为:150.
12.解:∵∠ABC=60°,∠ACB=60°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∵BC=58米,
∴AC=58米.
故答案为:58.
13.解:由勾股定理得:
AB=,BC=(m),
∴AB+BC=(m),
故答案为:3.
14.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
∴地毯的长度至少是12+5=17(米).
故答案为:17.
15.解:(1)由题意知AB=DE=25米,AC=24米,AD=4米,
在直角△ABC中,∠C=90°,
∴BC2+AC2=AB2,
∴米,
∴这个梯子底端离墙有7米;
(2)已知AD=4米,则CD=24﹣4=20(米),
在直角△CDE中,∠C=90°,
∴BD2+CE2=DE2,
∴(米),
∴BE=15﹣7=8(米),
答:梯子的底部在水平方向滑动了8m.
16.(1)解:设AE=x千米,则EB=(5﹣x)千米,
∵CA⊥AB,DB⊥AB,
∴∠CAE=∠EBD=90°,
在Rt△ACE和Rt△EBD中,由勾股定理得:AC2+AE2=EC2,BE2+DB2=ED2,
由题意得:EC=ED,
∴CA2+AE2=BE2+DB2,
∴32+x2=(5﹣x)2+22,
解得:x=2,
即AE=2千米,
故答案为:2;
(2)证明:由(1)得:AE=2千米,EB=3千米,
∵CA=3千米,DB=2千米,
∴CA=EB,AE=DB,
在△ACE和△BED中,
,
∴△ACE≌△BED(SAS),
∴EC=ED.
17.解:(1)∵9=3×3,12=4×3,16÷3≠5,
∴9,12,16不是“派生勾股数”;
∵10=5×2,24=12×2,26=13×2,
∴10,24,26是“派生勾股数”;
(2)勾股数3,4,5,把勾股数同时乘以3可得9,12,15,15﹣12=3,9,12,15是“新新勾股数”;
勾股数5,12,13,把勾股数同时乘以3可得15,36,39,39﹣36=3,15,36,39是“新新勾股数”;
勾股数7,24,25,把勾股数同时乘以3可得21,72,75,75﹣72=3,21,72,75是“新新勾股数”;
勾股数9,40,41,把勾股数同时乘以3可得27,120,123,123﹣120=3,27,120,123是“新新勾股数”;
勾股数11,60,61,把勾股数同时乘以3可得33,180,183,183﹣180=3,33,180,183是“新新勾股数”.
综上所述,斜边小于200的所有“新新勾股数”有9,12,15;15,36,39;21,72,75;27,120,123;33,180,183.
18.解:(1)如图所示:点E即为所求;
(2)如图所示:AB=;
(3)如图所示,△ABC即为所求.
19.解:(1)结合已知数据,可得:
OAn2=n,则Sn=;
(2)∵OAn2=n,
∴OA10=;
(3)S12+S22+S32+…+S102
=++++…+
=
=.
20.解:(1)如图1,AP⊥AB.
(2)如图2,△ABP的面积==3.
∴格点P使得△ABP的面积是3(答案不唯一).
(3)如图3,∵PA==,PB==,
∴格点P使得PA=PB(答案不唯一).
21.解:(1)若点A在线段PQ的垂直平分线上,则AP=AQ,
∵AP=t,AQ=12﹣3t,
∴t=12﹣3t,
解得:t=3,
答:当t=3时,点A在线段PQ的垂直平分线上;
(2)①若∠APQ=90°,
则△APQ是直角三角形,
∵∠A=60°,
∴∠AQP=30°,
∴AQ=2AP,
∴12﹣3t=2t,
∴t=,
②若∠AQP=90°,
则△APQ是直角三角形,
∵∠A=60°,
∴∠APQ=30°,
∴AP=2AQ,
∴t=2(12﹣3t),
∴t=.
∴当t=或时,△APQ是直角三角形.
22.解:(1)由图可得,点A到原点的距离为:,点A在原点右侧,
∴点A表示的实数为,
故答案为:,;
(2)①如图所示:
②表示数﹣与2﹣的点如图所示:
∴﹣<2﹣.
解:(1)由题意得四边形ABCD的面积为:
;
(2)证明:如图,连接AC,
∵AB2=32+22=13,BC2=32+22=13,AC2=52+12=26,且13+13=26,
∴AB2+BC2=AC2.
∴∠ABC=90°.
24.解:(1)如选择图1,四个相同的直角三角形的面积和再加上中间小四边形的面积等于大正方形的面积,
即
化简得:a2+b2=c2,
如选择图2,大正方形的面积等于四个相同的直角三角形的面积和再加上中间四边形的面积,
即,
化简得:a2+b2=c2.
(2)在图3中,
∵在直角三角形中,两条直角边的平方和等于斜边的平方,
即:a2+b2=c2.
∴S1+S2=a2+b2,S3=c2,
∴S1+S2=S3,
在图4中,
∵S1=π=,
S2==,
S3==,
∵a2+b2=c2,
∴S1+S2=S3,
在图5中,
∵S1=a×a=a2,
S2=b×b=,
S3=c×c=,
而a2+b2=c2,
∴S1+S2=S3,
∴三个图形中面积关系满足S1+S2=S3的有3个,
故答案为:3.
25.解:5s时,动点P运动的路程为2×5=10(cm),即点P运动到D点(点P与点D重合),
动点Q运动的路程为2.8×5=14(cm),
因为DC=BC=BA=5cm,
所以点Q在BA上,且BQ=14﹣10=4(cm).
在△BPQ中,因为BP=5cm,BQ=4cm,PQ=3cm,
所以BQ2+PQ2=42+32=25=BP2,
所以△BPQ是直角三角形,且∠BQP=90°,
所以∠AQP=180°﹣90°=90°,
所以两点运动5s时,△APQ是直角三角形.
