2021-2022学年鲁教版(五四制)八年级数学上册5.2平行四边形的判定 同步达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学上册5.2平行四边形的判定 同步达标测试(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学上册《5.2平行四边形的判定》同步达标测试(附答案)
一.选择题(共10小题,满分40分)
1.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种 B.4种 C.5种 D.6种
2.点A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个条件,不能使四边形ABCD是平行四边形的组合是( )
A.①② B.②③ C.①③ D.③④
3.下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.AB=AD,CB=CD
C.AB=CD,AD=BC D.∠B=∠C,∠A=∠D
4.下列给出的条件中,不能判定四边形ABCD是平行四边形的为( )
A.AB=CD,AD=BC B.AD=BC,AD∥BC
C.AB=CD,∠B=∠D D.AB∥CD,∠A=∠C
5.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.对角线相等四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行且相等的四边形是平行四边形
6.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.有两对邻角互补的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
7.如图,在 ABCD中,点E是AD边上一点,(点E和点A、D不重合),要使四边形EBCD为等腰梯形,还需要添加一个条件,下列条件中不一定符合要求的是( )
A.∠A=∠BEA B.AB=EB C.∠EBC=∠A D.AE=ED
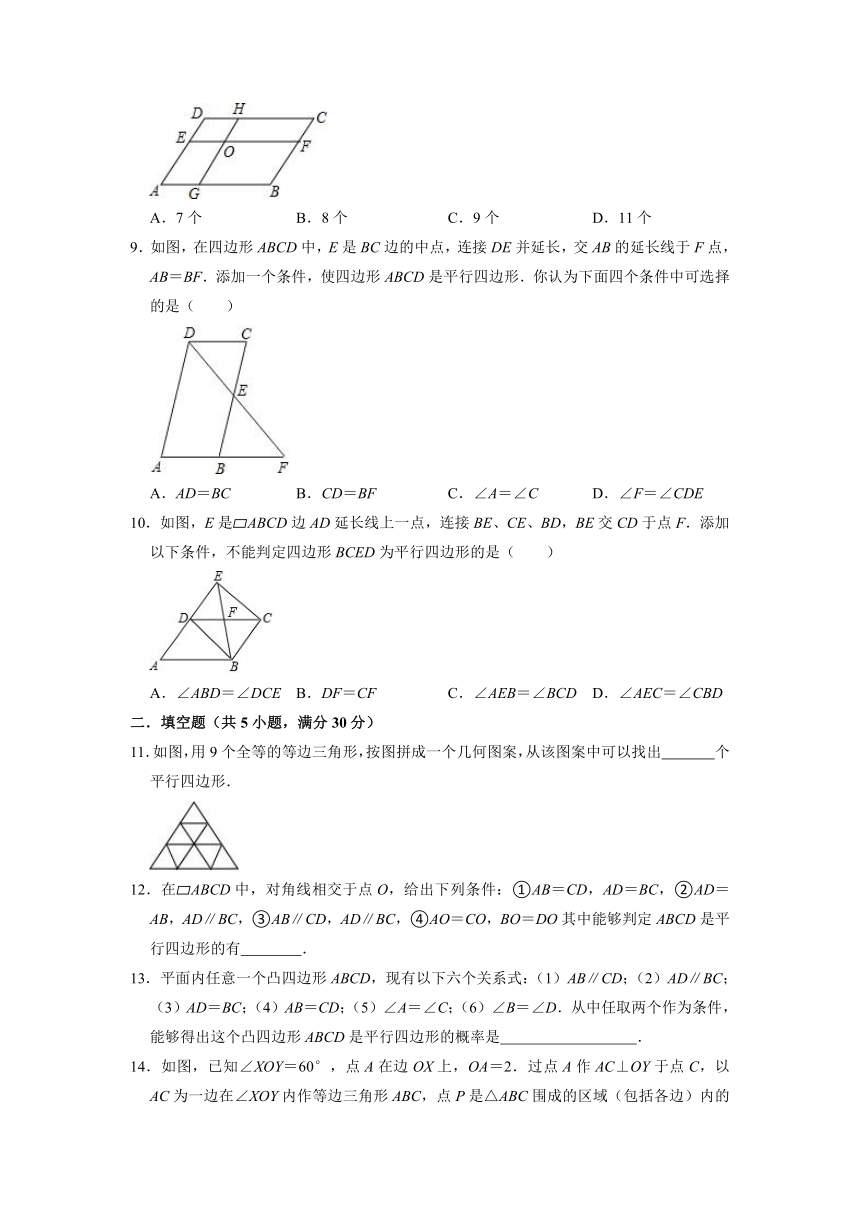
8.如图,在 ABCD中,EF∥AB,GH∥AD,EF与GH交于点O,则该图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
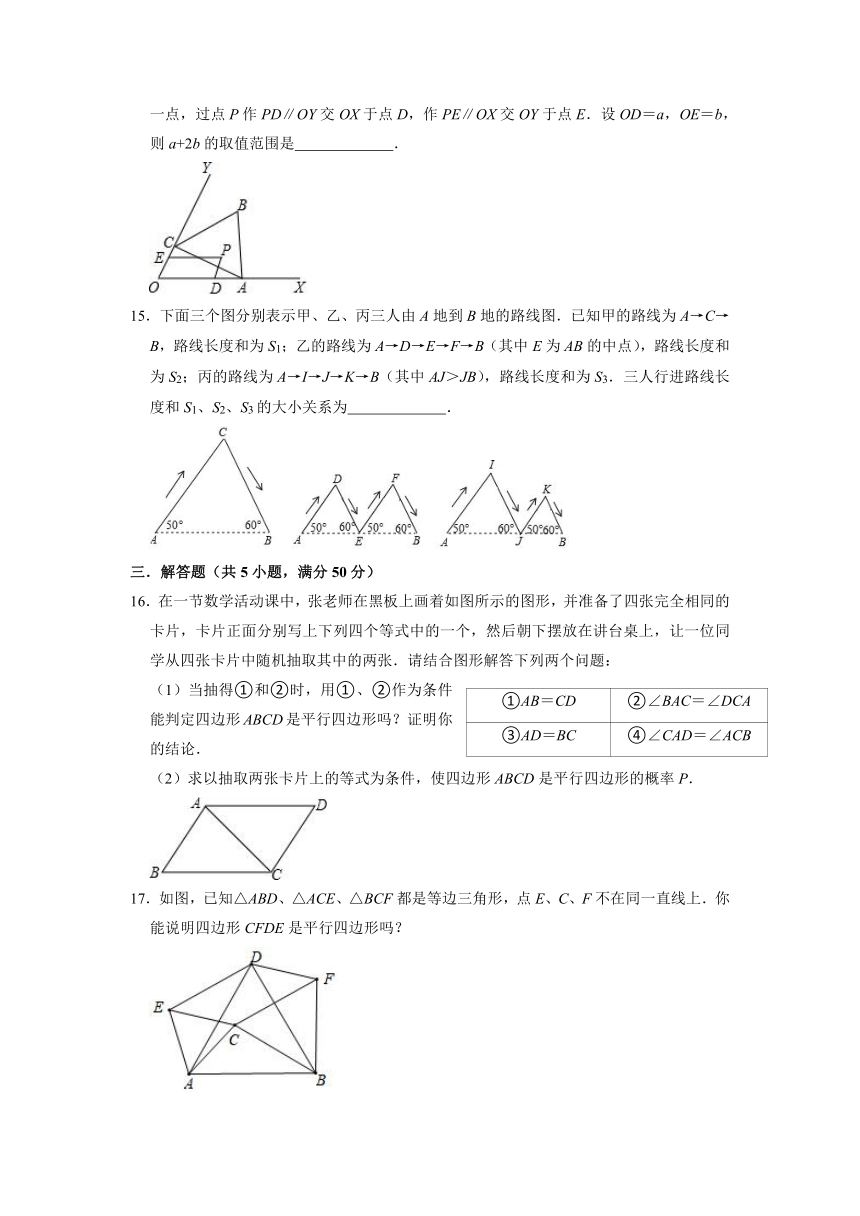
9.如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF C.∠A=∠C D.∠F=∠CDE
10.如图,E是 ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
二.填空题(共5小题,满分30分)
11.如图,用9个全等的等边三角形,按图拼成一个几何图案,从该图案中可以找出 个平行四边形.
12.在 ABCD中,对角线相交于点O,给出下列条件:①AB=CD,AD=BC,②AD=AB,AD∥BC,③AB∥CD,AD∥BC,④AO=CO,BO=DO其中能够判定ABCD是平行四边形的有 .
13.平面内任意一个凸四边形ABCD,现有以下六个关系式:(1)AB∥CD;(2)AD∥BC;(3)AD=BC;(4)AB=CD;(5)∠A=∠C;(6)∠B=∠D.从中任取两个作为条件,能够得出这个凸四边形ABCD是平行四边形的概率是 .
14.如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是 .
15.下面三个图分别表示甲、乙、丙三人由A地到B地的路线图.已知甲的路线为A→C→B,路线长度和为S1;乙的路线为A→D→E→F→B(其中E为AB的中点),路线长度和为S2;丙的路线为A→I→J→K→B(其中AJ>JB),路线长度和为S3.三人行进路线长度和S1、S2、S3的大小关系为 .
三.解答题(共5小题,满分50分)
16.在一节数学活动课中,张老师在黑板上画着如图所示的图形,并准备了四张完全相同的卡片,卡片正面分别写上下列四个等式中的一个,然后朝下摆放在讲台桌上,让一位同学从四张卡片中随机抽取其中的两张.请结合图形解答下列两个问题:
①AB=CD ②∠BAC=∠DCA
③AD=BC ④∠CAD=∠ACB
(1)当抽得①和②时,用①、②作为条件能判定四边形ABCD是平行四边形吗?证明你的结论.
(2)求以抽取两张卡片上的等式为条件,使四边形ABCD是平行四边形的概率P.
17.如图,已知△ABD、△ACE、△BCF都是等边三角形,点E、C、F不在同一直线上.你能说明四边形CFDE是平行四边形吗?
18.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.
19.如图,在平行四边形ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DEBF是平行四边形.
20.如图, ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
(1)求证:△AOE≌△COF;
(2)证明:四边形AECF是平行四边形.
参考答案
一.选择题(共10小题,满分40分)
1.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
2.解:A、∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形;故本选项错误;
B、②③不能判断四边形ABCD是平行四边形,可能是等腰梯形,故本选项正确;
C、∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形;故本选项错误;
D、∵BC=AD,AD∥BC,
∴四边形ABCD是平行四边形;故本选项错误;
故选:B.
3.解:A、根据AD∥CD,AD=BC不能判断四边形ABCD是平行四边形,故本选项错误;
B、根据AB=AD,BC=CD,不能判断四边形ABCD是平行四边形,故本选项错误;
C、根据AB=CD,AD=BC,得出四边形ABCD是平行四边形,故本选项正确;
D、根据∠B=∠C,∠A=∠D不能判断四边形ABCD是平行四边形,故本选项错误;
故选:C.
4.解:A、AB=CD,AD=BC,即四边形ABCD的两组对边相等,则该四边形是平行四边形,故本选项不符合题意;
B、AD=BC,AD∥BC,即四边形ABCD的一组对边平行且相等,则该四边形是平行四边形,故本选项不符合题意;
C、AB=CD,∠B=∠D,即四边形ABCD的一组对边相等,一组对角相等,所以不能判定该四边形是平行四边形.故本选项符合题意;
D、∵AB∥CD,
∴∠A+∠D=180°,∠B+∠C=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,故本选项不符合题意;
故选:C.
5.解:A、有一组邻边相等的平行四边形是菱形,本选项说法错误;
B、对角线相等平行四边形是矩形,本选项说法错误;
C、对角线垂直且相等的平行四边形是正方形,本选项说法错误;
D、一组对边平行且相等的四边形是平行四边形,本选项说法正确;
故选:D.
6.解:
A、∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,正确,故本选项不符合题意;
B、根据∠A+∠D=180°和∠B+∠C=180°只能推出AB∥CD,不一定是平行四边形,故本选项符合题意;
C、∵四边形ABCD的对角线AC、BD交于O,OA=OC,OB=OD,
∴四边形ABCD是平行四边形,正确,故本选项符合题意;
D、∵AB∥CD,
∴∠B+∠C=180°,
∵∠B=∠D,
∴∠C+∠D=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,正确,故本选项不符合题意;
故选:B.
7.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴DE≠BC,
∴四边形EBCD是梯形,
A、∵∠A=∠BEA,
∴AB=BE=CD,
∴梯形EBCD是等腰梯形,正确,不符合题意;
B、∵AB=BE=CD,
∴梯形EBCD是等腰梯形,正确,不符合题意;
C、∵AD∥BC,
∴∠AEB=∠EBC,
∵∠EBC=∠A,
∴∠A=∠BEA,
∴AB=BE=CD,
∴梯形EBCD是等腰梯形,正确,不符合题意;
D、根据AE=ED推不出符合等腰梯形的条件,错误,符合题意.
故选:D.
8.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边DEOH、DEFC、DHGA、BGOF、BGHC、BAEF、AGOE、CHOF和ABCD都是平行四边形,共9个.
故选:C.
9.解:添加:∠F=∠CDE,
理由:
∵∠F=∠CDE,
∴CD∥AB,
在△DEC与△FEB中,,
∴△DEC≌△FEB(AAS),
∴DC=BF,
∵AB=BF,
∴DC=AB,
∴四边形ABCD为平行四边形,
故选:D.
10.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴BCED为平行四边形,故A正确;
∵DE∥BC,
∴∠DEF=∠CBF,
在△DEF与△CBF中,,
∴△DEF≌△CBF(AAS),
∴EF=BF,
∵DF=CF,
∴四边形BCED为平行四边形,故B正确;
∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故C错误;
∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确,
故选:C.
二.填空题(共5小题,满分30分)
11.解:两个全等的等边三角形,以一边为对角线构成的四边形是平行四边形,这样的两个平行四边形又可组成较大的平行四边形,从该图案中可以找出15个平行四边形.
故答案为:15.
12.解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,∴①正确;
根据AD=AB,AD∥BC不能推出四边形ABCD是平行四边形,∴②错误;
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,∴③正确;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,∴④正确;
即其中能判定四边形ABCD是平行四边形的有①③④,
故答案为:①③④.
13.解:根据题意可得:从所给的六个关系式中任取两个作为条件,共15种取法;
其中①AB∥CD,AD∥BC;②AD=BC,AB=CD;③∠A=∠C,∠B=∠D;
④AB∥CD,AB=CD;⑤AD∥BC,AD=BC;
⑥AB∥CD,∠A=∠C;⑦AB∥CD,∠B=∠D;⑧AD∥BC,∠A=∠C;⑨AD∥BC,∠B=∠D,
共9种能得出这个四边形ABCD是平行四边形,
故其概率为=.
故答案为:.
14.解:如图1,过P作PH⊥OY交于点H,
∵PD∥OY,PE∥OX,
∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,
∴EP=OD=a,
Rt△HEP中,∠EPH=30°,
∴EH=EP=a,
∴a+2b=2(a+b)=2(EH+EO)=2OH,
当P在AC边上时,H与C重合,此时OH的最小值=OC=OA=1,即a+2b的最小值是2;
当P在点B时,如图2,OC=1,AC=BC=,
Rt△CHP中,∠HCP=30°,
∴PH=,CH=,
则OH的最大值是:OC+CH=1+=,即(a+2b)的最大值是5,
∴2≤a+2b≤5.
15.解:如图所示,延长AD,BF交于点G,延长AI,BK交于点H,
依据ASA可知,△ABC≌△ABG≌△ABH,
∴AC=AG=AH,BC=BG=BH,
∵∠A=∠BEF=50°,∠AED=∠B=60°,
∴DG∥EF,DE∥GF,
∴四边形DEFG是平行四边形,
∴EF=DG,DE=FG,
同理可得IJ=HK,JK=IH,
∴S2=AD+DE+EF+BF=AD+FG+DG+BF=AG+BG=AC+BC,
S3=AI+IJ+JK+BK=AI+KH+IH+BK=AH+BH=AC+BC,
又∵S1=AC+BC,
∴S1=S2=S3,
故答案为:S1=S2=S3.
三.解答题(共5小题,满分40分)
16.解:(1)答:是平行四边形
证明:∵∠BAC=∠DCA∴AB∥CD
∵AB=CD∴四边形ABCD是平行四边形
(2)解:在四张卡片中随机抽取两张,可能情况有①和②,①和③,①和④,②和③,②和④,③和④共6种情况.
其中①和②,①和④,②和③,③和④作为条件,四边形ABCD是平行四边形,共4种.
∴四边形ABCD是平行四边形的概率是P=
17.证明:∵△ABD、△ACE都是等边三角形,
∴AD=AB,AE=AC,∠BAD=∠CAE=60°,
∴∠BAC=∠DAE,
∴△BAC≌△DAE(SAS),
∴DE=BC,
又∵等边三角形BCF中,CF=BC,
∴DE=CF,
同理可得,DF=EC,
∴四边形DECF是平行四边形.
18.证明:∵DE=DC,
∴∠DEC=∠C.
∵∠B=∠C,
∴∠B=∠DEC,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是平行四边形.
∴AD=BE.
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠CDB=∠ABD,
∵DF平分∠CDB,BE平分∠ABD,
∴∠FDB=∠CDB,∠EBD=∠ABD,
∴∠FDB=∠EBD,
∴DF∥BE,
∵AD∥BC,即ED∥BF,
∴四边形DEBF是平行四边形.
20.解:(1)∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.
∵在△AOE与△COF中,
,
∴△AOE≌△COF(AAS);
(2)如图,连接EC、AF,
由(1)可知△AOE≌△COF,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形.
一.选择题(共10小题,满分40分)
1.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种 B.4种 C.5种 D.6种
2.点A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个条件,不能使四边形ABCD是平行四边形的组合是( )
A.①② B.②③ C.①③ D.③④
3.下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.AB=AD,CB=CD
C.AB=CD,AD=BC D.∠B=∠C,∠A=∠D
4.下列给出的条件中,不能判定四边形ABCD是平行四边形的为( )
A.AB=CD,AD=BC B.AD=BC,AD∥BC
C.AB=CD,∠B=∠D D.AB∥CD,∠A=∠C
5.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.对角线相等四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行且相等的四边形是平行四边形
6.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.有两对邻角互补的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
7.如图,在 ABCD中,点E是AD边上一点,(点E和点A、D不重合),要使四边形EBCD为等腰梯形,还需要添加一个条件,下列条件中不一定符合要求的是( )
A.∠A=∠BEA B.AB=EB C.∠EBC=∠A D.AE=ED
8.如图,在 ABCD中,EF∥AB,GH∥AD,EF与GH交于点O,则该图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
9.如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF C.∠A=∠C D.∠F=∠CDE
10.如图,E是 ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
二.填空题(共5小题,满分30分)
11.如图,用9个全等的等边三角形,按图拼成一个几何图案,从该图案中可以找出 个平行四边形.
12.在 ABCD中,对角线相交于点O,给出下列条件:①AB=CD,AD=BC,②AD=AB,AD∥BC,③AB∥CD,AD∥BC,④AO=CO,BO=DO其中能够判定ABCD是平行四边形的有 .
13.平面内任意一个凸四边形ABCD,现有以下六个关系式:(1)AB∥CD;(2)AD∥BC;(3)AD=BC;(4)AB=CD;(5)∠A=∠C;(6)∠B=∠D.从中任取两个作为条件,能够得出这个凸四边形ABCD是平行四边形的概率是 .
14.如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是 .
15.下面三个图分别表示甲、乙、丙三人由A地到B地的路线图.已知甲的路线为A→C→B,路线长度和为S1;乙的路线为A→D→E→F→B(其中E为AB的中点),路线长度和为S2;丙的路线为A→I→J→K→B(其中AJ>JB),路线长度和为S3.三人行进路线长度和S1、S2、S3的大小关系为 .
三.解答题(共5小题,满分50分)
16.在一节数学活动课中,张老师在黑板上画着如图所示的图形,并准备了四张完全相同的卡片,卡片正面分别写上下列四个等式中的一个,然后朝下摆放在讲台桌上,让一位同学从四张卡片中随机抽取其中的两张.请结合图形解答下列两个问题:
①AB=CD ②∠BAC=∠DCA
③AD=BC ④∠CAD=∠ACB
(1)当抽得①和②时,用①、②作为条件能判定四边形ABCD是平行四边形吗?证明你的结论.
(2)求以抽取两张卡片上的等式为条件,使四边形ABCD是平行四边形的概率P.
17.如图,已知△ABD、△ACE、△BCF都是等边三角形,点E、C、F不在同一直线上.你能说明四边形CFDE是平行四边形吗?
18.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.
19.如图,在平行四边形ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DEBF是平行四边形.
20.如图, ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
(1)求证:△AOE≌△COF;
(2)证明:四边形AECF是平行四边形.
参考答案
一.选择题(共10小题,满分40分)
1.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
2.解:A、∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形;故本选项错误;
B、②③不能判断四边形ABCD是平行四边形,可能是等腰梯形,故本选项正确;
C、∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形;故本选项错误;
D、∵BC=AD,AD∥BC,
∴四边形ABCD是平行四边形;故本选项错误;
故选:B.
3.解:A、根据AD∥CD,AD=BC不能判断四边形ABCD是平行四边形,故本选项错误;
B、根据AB=AD,BC=CD,不能判断四边形ABCD是平行四边形,故本选项错误;
C、根据AB=CD,AD=BC,得出四边形ABCD是平行四边形,故本选项正确;
D、根据∠B=∠C,∠A=∠D不能判断四边形ABCD是平行四边形,故本选项错误;
故选:C.
4.解:A、AB=CD,AD=BC,即四边形ABCD的两组对边相等,则该四边形是平行四边形,故本选项不符合题意;
B、AD=BC,AD∥BC,即四边形ABCD的一组对边平行且相等,则该四边形是平行四边形,故本选项不符合题意;
C、AB=CD,∠B=∠D,即四边形ABCD的一组对边相等,一组对角相等,所以不能判定该四边形是平行四边形.故本选项符合题意;
D、∵AB∥CD,
∴∠A+∠D=180°,∠B+∠C=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,故本选项不符合题意;
故选:C.
5.解:A、有一组邻边相等的平行四边形是菱形,本选项说法错误;
B、对角线相等平行四边形是矩形,本选项说法错误;
C、对角线垂直且相等的平行四边形是正方形,本选项说法错误;
D、一组对边平行且相等的四边形是平行四边形,本选项说法正确;
故选:D.
6.解:
A、∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,正确,故本选项不符合题意;
B、根据∠A+∠D=180°和∠B+∠C=180°只能推出AB∥CD,不一定是平行四边形,故本选项符合题意;
C、∵四边形ABCD的对角线AC、BD交于O,OA=OC,OB=OD,
∴四边形ABCD是平行四边形,正确,故本选项符合题意;
D、∵AB∥CD,
∴∠B+∠C=180°,
∵∠B=∠D,
∴∠C+∠D=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,正确,故本选项不符合题意;
故选:B.
7.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴DE≠BC,
∴四边形EBCD是梯形,
A、∵∠A=∠BEA,
∴AB=BE=CD,
∴梯形EBCD是等腰梯形,正确,不符合题意;
B、∵AB=BE=CD,
∴梯形EBCD是等腰梯形,正确,不符合题意;
C、∵AD∥BC,
∴∠AEB=∠EBC,
∵∠EBC=∠A,
∴∠A=∠BEA,
∴AB=BE=CD,
∴梯形EBCD是等腰梯形,正确,不符合题意;
D、根据AE=ED推不出符合等腰梯形的条件,错误,符合题意.
故选:D.
8.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边DEOH、DEFC、DHGA、BGOF、BGHC、BAEF、AGOE、CHOF和ABCD都是平行四边形,共9个.
故选:C.
9.解:添加:∠F=∠CDE,
理由:
∵∠F=∠CDE,
∴CD∥AB,
在△DEC与△FEB中,,
∴△DEC≌△FEB(AAS),
∴DC=BF,
∵AB=BF,
∴DC=AB,
∴四边形ABCD为平行四边形,
故选:D.
10.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴BCED为平行四边形,故A正确;
∵DE∥BC,
∴∠DEF=∠CBF,
在△DEF与△CBF中,,
∴△DEF≌△CBF(AAS),
∴EF=BF,
∵DF=CF,
∴四边形BCED为平行四边形,故B正确;
∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故C错误;
∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确,
故选:C.
二.填空题(共5小题,满分30分)
11.解:两个全等的等边三角形,以一边为对角线构成的四边形是平行四边形,这样的两个平行四边形又可组成较大的平行四边形,从该图案中可以找出15个平行四边形.
故答案为:15.
12.解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,∴①正确;
根据AD=AB,AD∥BC不能推出四边形ABCD是平行四边形,∴②错误;
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,∴③正确;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,∴④正确;
即其中能判定四边形ABCD是平行四边形的有①③④,
故答案为:①③④.
13.解:根据题意可得:从所给的六个关系式中任取两个作为条件,共15种取法;
其中①AB∥CD,AD∥BC;②AD=BC,AB=CD;③∠A=∠C,∠B=∠D;
④AB∥CD,AB=CD;⑤AD∥BC,AD=BC;
⑥AB∥CD,∠A=∠C;⑦AB∥CD,∠B=∠D;⑧AD∥BC,∠A=∠C;⑨AD∥BC,∠B=∠D,
共9种能得出这个四边形ABCD是平行四边形,
故其概率为=.
故答案为:.
14.解:如图1,过P作PH⊥OY交于点H,
∵PD∥OY,PE∥OX,
∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,
∴EP=OD=a,
Rt△HEP中,∠EPH=30°,
∴EH=EP=a,
∴a+2b=2(a+b)=2(EH+EO)=2OH,
当P在AC边上时,H与C重合,此时OH的最小值=OC=OA=1,即a+2b的最小值是2;
当P在点B时,如图2,OC=1,AC=BC=,
Rt△CHP中,∠HCP=30°,
∴PH=,CH=,
则OH的最大值是:OC+CH=1+=,即(a+2b)的最大值是5,
∴2≤a+2b≤5.
15.解:如图所示,延长AD,BF交于点G,延长AI,BK交于点H,
依据ASA可知,△ABC≌△ABG≌△ABH,
∴AC=AG=AH,BC=BG=BH,
∵∠A=∠BEF=50°,∠AED=∠B=60°,
∴DG∥EF,DE∥GF,
∴四边形DEFG是平行四边形,
∴EF=DG,DE=FG,
同理可得IJ=HK,JK=IH,
∴S2=AD+DE+EF+BF=AD+FG+DG+BF=AG+BG=AC+BC,
S3=AI+IJ+JK+BK=AI+KH+IH+BK=AH+BH=AC+BC,
又∵S1=AC+BC,
∴S1=S2=S3,
故答案为:S1=S2=S3.
三.解答题(共5小题,满分40分)
16.解:(1)答:是平行四边形
证明:∵∠BAC=∠DCA∴AB∥CD
∵AB=CD∴四边形ABCD是平行四边形
(2)解:在四张卡片中随机抽取两张,可能情况有①和②,①和③,①和④,②和③,②和④,③和④共6种情况.
其中①和②,①和④,②和③,③和④作为条件,四边形ABCD是平行四边形,共4种.
∴四边形ABCD是平行四边形的概率是P=
17.证明:∵△ABD、△ACE都是等边三角形,
∴AD=AB,AE=AC,∠BAD=∠CAE=60°,
∴∠BAC=∠DAE,
∴△BAC≌△DAE(SAS),
∴DE=BC,
又∵等边三角形BCF中,CF=BC,
∴DE=CF,
同理可得,DF=EC,
∴四边形DECF是平行四边形.
18.证明:∵DE=DC,
∴∠DEC=∠C.
∵∠B=∠C,
∴∠B=∠DEC,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是平行四边形.
∴AD=BE.
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠CDB=∠ABD,
∵DF平分∠CDB,BE平分∠ABD,
∴∠FDB=∠CDB,∠EBD=∠ABD,
∴∠FDB=∠EBD,
∴DF∥BE,
∵AD∥BC,即ED∥BF,
∴四边形DEBF是平行四边形.
20.解:(1)∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.
∵在△AOE与△COF中,
,
∴△AOE≌△COF(AAS);
(2)如图,连接EC、AF,
由(1)可知△AOE≌△COF,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形.
