2021-2022学年鲁教版(五四制)七年级数学上册第5章位置与坐标 单元综合测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册第5章位置与坐标 单元综合测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 232.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 23:48:09 | ||
图片预览




文档简介
2021-2022学年鲁教版七年级数学上册《第5章位置与坐标》单元综合测评(附答案)
一.选择题(共10小题,满分40分)
1.在平面直角坐标系中,点A(a,1)与点B (5,﹣1)关于x轴对称,则( )
A.a=1 B.a=﹣1 C.a=5 D.a=﹣5
2.在平面直角坐标系xOy中,A、B两点关于y轴对称,若A的坐标是(2,﹣8),则点B的坐标是( )
A.(8,2) B.(2,8) C.(﹣2,8) D.(﹣2,﹣8)
3.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
4.在直角坐标系中,点P(6,8)到原点的距离为( )
A.10 B.﹣10 C.±10 D.12
5.在平面直角坐标系中,若点A(a,﹣b)在第三象限,则点B(﹣ab,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若线段AB∥x轴且AB=3,点A的坐标为(2,1),则点B的坐标为( )
A.(5,1) B.(﹣1,1)
C.(5,1)或(﹣1,1) D.(2,4)或(2,﹣2)
7.将点P(﹣2,﹣3)向左平移3个长度单位,再向上平移2个长度单位得到点Q,则点Q的坐标是( )
A.(1,﹣3) B.(﹣2,1) C.(﹣5,﹣1) D.(﹣5,5)
8.如图,在平面直角坐标系中,A(1,0),B(﹣2,4),AB绕点A顺时针旋转90°得到AC,则点C的坐标是( )
A.(4,3) B.(4,4) C.(5,3) D.(5,4)
9.若点M(a+3,2a﹣4)在x轴上,则点M的坐标为( )
A.(0,﹣10) B.(5,0) C.(10,0) D.(0,5)
10.平面直角坐标系中,已知点P(a,3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,3) B.(a,﹣3) C.(﹣a+2,3) D.(﹣a+4,3)
二.填空题(共8小题,满分32分)
11.已知|m+5|+=0,点P(m,n)关于x轴的对称点的坐标是 .
12.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)的坐标为 .
13.若点(2,a)与点(b,﹣1)关于原点对称,则ab= .
14.在平面直角坐标系中,已知两点坐标A(m﹣1,3),B(1,m2﹣1).若AB∥x轴,则m的值是 .
15.平面直角坐标系中,将点A(﹣1,2)先向左平移2个单位,再向上平移1个单位后得到的点A1的坐标为 .
16.在平面直角坐标系中,若点M(1﹣m,m+2)与点N(2m+3,m+2)之间的距离是5,则m= .
17.如图,在平面直角坐标系中,将点P(4,6)绕坐标原点O顺时针旋转90°得到点Q,则点Q的坐标为 .
18.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线,构成如图所示的“圆”坐标系,点A、B的坐标分别表示为(5,0°)、(4,300°),则点C的坐标表示为 .
三.解答题(共6小题,满分48分)
19.如图,在平面直角坐标系中,点A、B、C的坐标分别为A(2,﹣1),B(4,3),C(1,2).将△ABC先向左平移4个单位,再向下平移2个单位得到△A1B1C1.
(1)请在图中画出△A1B1C1;
(2)写出平移后的△A1B1C1三个顶点的坐标;
A1( , )
B1( , )
C1( , )
(3)求△ABC的面积.
20.已知点P(2a﹣2,a+5),解答下列各题.
(1)点P在x轴上,求出点P的坐标.
(2)点Q的坐标为(4,5),直线PQ∥y轴;求出点P的坐标.
(3)若点P在第二象限,且它到x轴、y轴的距离相等,求a2020+2020的值.
21.在平面直角坐标系中,点A(6,0),点B(0,8),把△AOB绕原点O逆时针旋转,得△COD,其中,点C,D分别为点A,B旋转后的对应点.记旋转角为α(0°<α<360°).
(1)如图,当α=45°时,求点C的坐标;
(2)当CD∥x轴时,求点C的坐标(直接写出结果即可).
22.先阅读下列一段文字,再回答后面的问题:已知在平面直角坐标系内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(1,3),B(﹣3,﹣5),试求A,B两点间的距离;
(2)已知线段MN∥y轴,MN=4,若点M的坐标为(2,﹣1),试求点N的坐标;
(3)已知一个三角形各顶点坐标为D(0,6),E(﹣3,2),F(3,2),你能判定此三角形的形状吗?说明理由.
23.综合与实践
问题背景
如图,在平面直角坐标系中,点A的坐标为(﹣3,5),点B的坐标为(0,1),点C的坐标为(4,5),将线段AB沿AC方向平移,平移距离为线段AC的长度.
动手操作
(1)画出AB平移后的线段CD,直接写出B的对应点D的坐标;
探究证明
(2)连接BD,试探究∠BAC,∠BDC的数量关系,并证明你的结论;
拓展延伸
(3)若点E在线段BD上,连接AD,AE,且满足∠EAD=∠CAD,请求出∠ADB:∠AEB的值,并写出推理过程.
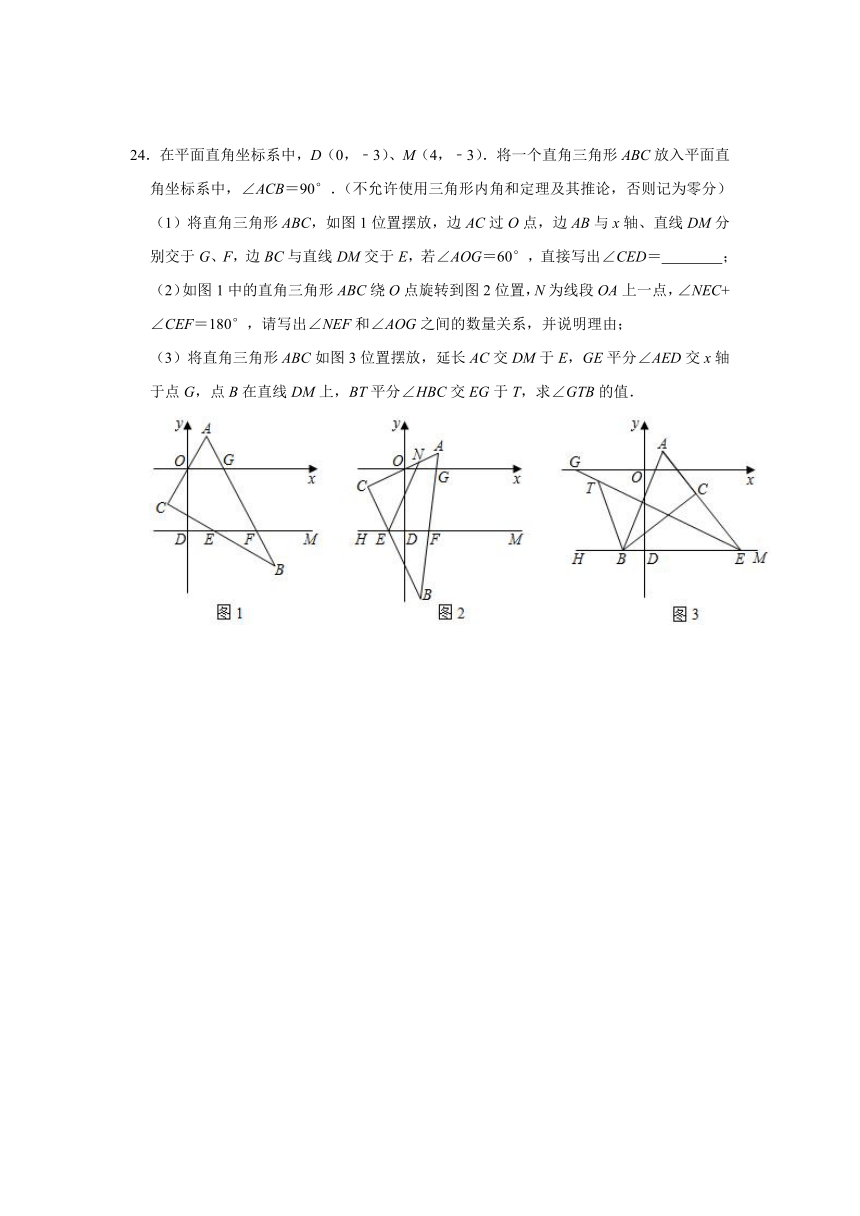
24.在平面直角坐标系中,D(0,﹣3)、M(4,﹣3).将一个直角三角形ABC放入平面直角坐标系中,∠ACB=90°.(不允许使用三角形内角和定理及其推论,否则记为零分)
(1)将直角三角形ABC,如图1位置摆放,边AC过O点,边AB与x轴、直线DM分别交于G、F,边BC与直线DM交于E,若∠AOG=60°,直接写出∠CED= ;
(2)如图1中的直角三角形ABC绕O点旋转到图2位置,N为线段OA上一点,∠NEC+∠CEF=180°,请写出∠NEF和∠AOG之间的数量关系,并说明理由;
(3)将直角三角形ABC如图3位置摆放,延长AC交DM于E,GE平分∠AED交x轴于点G,点B在直线DM上,BT平分∠HBC交EG于T,求∠GTB的值.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵点A(a,1)与点B (5,﹣1)关于x轴对称,
∴a=5,
故选:C.
2.解:∵A、B两点关于y轴对称,A的坐标是(2,﹣8),
∴点B的坐标是(﹣2,﹣8),
故选:D.
3.解:∵点P位于第二象限,
∴点的横坐标为负数,纵坐标为正数,
∵点距离x轴5个单位长度,距离y轴3个单位长度,
∴点的坐标为(﹣3,5).
故选:D.
4.解:点P(6,8)到原点的距离为:=10,故选:A.
5.解:∵点A(a,﹣b)在第三象限,
∴a<0,﹣b<0,
∴b>0,
∴﹣ab>0,
∴点B(﹣ab,b)所在的象限是第一象限.
故选:A.
6.解:∵AB∥x轴,点A的坐标为(2,1),
∴A、B两点纵坐标都是1,
又∵AB=3,
∴当B点在A点左边时,B的坐标为(﹣1,1),
当B点在A点右边时,B的坐标为(5,1).
故选:C.
7.解:根据题意,点Q的横坐标为:﹣2﹣3=﹣5;纵坐标为﹣3+2=﹣1;
即点Q的坐标是(﹣5,﹣1).
故选:C.
8.解:如图,过点B作BE⊥x轴于E,过点C作CF⊥x轴于F.
∵A(1,0),B(﹣2,4),
∴OA=1,BE=4,OE=2,AE=3,
∵∠AEB=∠AFC=∠BAC=90°,
∴∠B+∠BAE=90°,∠BAE+∠CAF=90°,
∴∠B=∠CAF,
∵AB=AC,
∴△BEA≌△AFC(AAS),
∴CF=AE=3,AF=BE=4,OF=1+4=5,
∴C(5,3),
故选:C.
9.解:∵点M(a+3,2a﹣4)在x轴上,
∴2a﹣4=0,
解得:a=2,
则a+3=5,
∴点M的坐标为:(5,0).
故选:B.
10.解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a,3)在第二象限,
∴a到直线m的距离为:2﹣a,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a,
故P点对称的点的坐标是:(﹣a+4,3).
故选:D.
二.填空题(共8小题,满分32分)
11.解:由于|m+5|+=0,
所以 m+5=0,n﹣3=0,
所以 m=﹣5,n=3,
所以 点P的坐标是(﹣5,3).
所以点P(m,n)关于x轴的对称点的坐标是 (﹣5,﹣3).
故答案是:(﹣5,﹣3).
12.解:∵A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,
∴a﹣5=0,b+3=0,
解得:a=5,b=﹣3,
∴C(a,b)的坐标为:(5,﹣3).
故答案为:(5,﹣3).
13.解:∵点(2,a)与点(b,﹣1)关于原点对称,
∴a=1,b=﹣2,
∴ab=﹣2.
故答案为:﹣2.
14.解:∵A(m﹣1,3),B (1,m2﹣1).AB∥x轴,
∴m2﹣1=3,
解得:m=±2;
当m=2时,A,B两点坐标都是(1,3),不符合题意,舍去,
∴m=﹣2;
故答案为:﹣2.
15.解:∵将点A(﹣1,2)先向左平移2个单位,横坐标﹣2,
再向上平移1个单位纵坐标+1,
∴平移后得到的点A1的坐标为:(﹣3,3).
故答案为:(﹣3,3).
16.解:∵点M(1﹣m,m+2)与点N(2m+3,m+2)的纵坐标都是m+2,
∴MN∥x轴,
点N在点M的左边时,1﹣m﹣(2m+3)=5,解得m=﹣,
点N在点M的右边时,2m+3﹣1+m=5,解得m=1,
综上所述,m的值是﹣或1.
故答案为:﹣或1.
17.解:作图如下,
∵∠MPO+∠POM=90°,∠QON+∠POM=90°,
∴∠MPO=∠QON,
在△PMO和△ONQ中,
,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
∵P点坐标为(4,6),
∴Q点坐标为(6,﹣4),
故答案为(6,﹣4).
18.解:如图所示:点C的坐标表示为(3,240°).
故答案为:(3,240°).
三.解答题(共6小题,满分48分)
19.解:(1)如图所示:△A1B1C1即为所求;
(2)A1(﹣2,﹣3),B1(0,1),C1(﹣3,0);
故答案为:﹣2,﹣3;0,1;﹣3,0.
(3)如图可得:
S△ABC=S长方形EFGB﹣S△BEC﹣S△CFA﹣S△AGB
=BE EF﹣EB CE﹣CF FA﹣AG BG
=3×4﹣×3×1﹣×3×1﹣×2×4
=5.
20.解:(1)∵点P在x轴上,
∴a+5=0,
∴a=﹣5,
∴2a﹣2=2×(﹣5)﹣2=﹣12,
∴点P的坐标为(﹣12,0).
(2)点Q的坐标为(4,5),直线PQ∥y轴,
∴2a﹣2=4,
∴a=3,
∴a+5=8,
∴点P的坐标为(4,8).
(3)∵点P在第二象限,且它到x轴、y轴的距离相等,
∴2a﹣2=﹣(a+5),
∴2a﹣2+a+5=0,
∴a=﹣1,
∴a2020+2020=(﹣1)2020+2020=2021.
∴a2020+2020的值为2021.
21.解:(1)如图,过点C作CE⊥OA于E.
∵A(6,0),
∵OA=OC=6,
∵∠COE=45°,
∴EC=OE=3,
∴C(3,3).
(2)如图,CD在x轴上方时,设CD交y轴于F,过点D作DT⊥x轴于T.
∵CD∥x轴,
∴CD⊥OF,
∵OB=OD=8,OC=OA=6,
∴CD===10,
∴DT=OF==,
∴OT===,CF=10﹣=,
∴C(,),
当CD在x轴下方时,同法可得C(﹣,﹣).
综上所述,满足条件的点C的坐标为(,)或(﹣,﹣).
22.解:(1)A,B两点间的距离==4;
(2)∵线段MN∥y轴,
∴M、N的横坐标相同,
设N(2,t),
∴|t+1|=4,解得t=3或﹣5,
∴N点坐标为(2,3)或(2,﹣5);
(3)△DEF为等腰三角形.
理由如下:
∵D(0,6),E(﹣3,2),F(3,2),
∴DE==5,DF==5,EF==6,
∴DE=DF,
∴△DEF为等腰三角形.
23.解:(1)如图,CD为所作,
因为AB向右平移7个单位,
所以D点坐标为(7,1);
(2)∠BAC=∠BDC.
理由如下:
∵AB平移后的线段CD,
∴AB∥CD,AC∥BD,
∴∠ABD+∠BDC=180°,∠BAC+∠ABD=180°,
∴∠BAC=∠BDC;
(3)∠ADB:∠AEB=1:2;
理由如下:∵AC∥BD,
∴∠CAD=∠ADB,∠AEB=∠CAE,
∵∠EAD=∠CAD,
∴∠CAE=2∠CAD,
∴∠AEB=2∠ADB,
即∠ADB:∠AEB=1:2.
24.解:(1)如图1,过C作CK∥x轴,则∠AOG=∠ACK=60°,
∵∠ACB=90°,
∴∠BCK=90°﹣60°=30°,
∵D(0,﹣3),M(4,﹣3)
∴DM∥x轴
∵CK∥x轴,
∴DM∥CK,
∴∠BCK=∠CED=30°,
故答案为:30°;
(2)∠NEF=2∠AOG,理由如下:
如图2,过点C作CK∥x轴,
∵D(0,﹣3),M(4,﹣3),
∴DM∥x轴,
∵CK∥x轴,
∴DM∥CK∥x轴,
∴∠AOG=∠ACK,
∵∠KCE+∠CEF=180°,∠NEC+∠CEF=180°,
∴∠KCE=∠NEC,
∵CK∥DM,
∴∠KCE=∠CEH,
∴∠NEC=∠CEH,
∵∠NEF=180°﹣∠NEC﹣∠CEH,
∴∠NEF=180°﹣2∠KCE,
∵∠AOG=∠ACK=90°﹣∠KCE,
∴∠NEF=2∠AOG;
(3)如图3,作TL∥MH,CK∥MH,
∵TL∥MH,CK∥MH,DM∥OG,
∴TL∥CK∥DM∥OG,
∵GE平分∠AED,BT平分∠HBC,
∴可设∠AEG=∠GEB=α,∠HBT=∠TBC=β,
可得∠AEB=2α,∠CBE=180°﹣2β,
∴∠ACB=180﹣2β+2α,
又∵∠ACB=90°,
∴180﹣2β+2α=90°,
∴β﹣α=45°,
∵TL∥MH,
∴∠GTL=∠GEB=α,∠BTL=180°﹣∠TBH=180°﹣β,
∴∠GTB=α+180°﹣β,
∴∠GTB=180°﹣(β﹣α)=135°.
一.选择题(共10小题,满分40分)
1.在平面直角坐标系中,点A(a,1)与点B (5,﹣1)关于x轴对称,则( )
A.a=1 B.a=﹣1 C.a=5 D.a=﹣5
2.在平面直角坐标系xOy中,A、B两点关于y轴对称,若A的坐标是(2,﹣8),则点B的坐标是( )
A.(8,2) B.(2,8) C.(﹣2,8) D.(﹣2,﹣8)
3.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
4.在直角坐标系中,点P(6,8)到原点的距离为( )
A.10 B.﹣10 C.±10 D.12
5.在平面直角坐标系中,若点A(a,﹣b)在第三象限,则点B(﹣ab,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若线段AB∥x轴且AB=3,点A的坐标为(2,1),则点B的坐标为( )
A.(5,1) B.(﹣1,1)
C.(5,1)或(﹣1,1) D.(2,4)或(2,﹣2)
7.将点P(﹣2,﹣3)向左平移3个长度单位,再向上平移2个长度单位得到点Q,则点Q的坐标是( )
A.(1,﹣3) B.(﹣2,1) C.(﹣5,﹣1) D.(﹣5,5)
8.如图,在平面直角坐标系中,A(1,0),B(﹣2,4),AB绕点A顺时针旋转90°得到AC,则点C的坐标是( )
A.(4,3) B.(4,4) C.(5,3) D.(5,4)
9.若点M(a+3,2a﹣4)在x轴上,则点M的坐标为( )
A.(0,﹣10) B.(5,0) C.(10,0) D.(0,5)
10.平面直角坐标系中,已知点P(a,3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,3) B.(a,﹣3) C.(﹣a+2,3) D.(﹣a+4,3)
二.填空题(共8小题,满分32分)
11.已知|m+5|+=0,点P(m,n)关于x轴的对称点的坐标是 .
12.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)的坐标为 .
13.若点(2,a)与点(b,﹣1)关于原点对称,则ab= .
14.在平面直角坐标系中,已知两点坐标A(m﹣1,3),B(1,m2﹣1).若AB∥x轴,则m的值是 .
15.平面直角坐标系中,将点A(﹣1,2)先向左平移2个单位,再向上平移1个单位后得到的点A1的坐标为 .
16.在平面直角坐标系中,若点M(1﹣m,m+2)与点N(2m+3,m+2)之间的距离是5,则m= .
17.如图,在平面直角坐标系中,将点P(4,6)绕坐标原点O顺时针旋转90°得到点Q,则点Q的坐标为 .
18.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线,构成如图所示的“圆”坐标系,点A、B的坐标分别表示为(5,0°)、(4,300°),则点C的坐标表示为 .
三.解答题(共6小题,满分48分)
19.如图,在平面直角坐标系中,点A、B、C的坐标分别为A(2,﹣1),B(4,3),C(1,2).将△ABC先向左平移4个单位,再向下平移2个单位得到△A1B1C1.
(1)请在图中画出△A1B1C1;
(2)写出平移后的△A1B1C1三个顶点的坐标;
A1( , )
B1( , )
C1( , )
(3)求△ABC的面积.
20.已知点P(2a﹣2,a+5),解答下列各题.
(1)点P在x轴上,求出点P的坐标.
(2)点Q的坐标为(4,5),直线PQ∥y轴;求出点P的坐标.
(3)若点P在第二象限,且它到x轴、y轴的距离相等,求a2020+2020的值.
21.在平面直角坐标系中,点A(6,0),点B(0,8),把△AOB绕原点O逆时针旋转,得△COD,其中,点C,D分别为点A,B旋转后的对应点.记旋转角为α(0°<α<360°).
(1)如图,当α=45°时,求点C的坐标;
(2)当CD∥x轴时,求点C的坐标(直接写出结果即可).
22.先阅读下列一段文字,再回答后面的问题:已知在平面直角坐标系内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(1,3),B(﹣3,﹣5),试求A,B两点间的距离;
(2)已知线段MN∥y轴,MN=4,若点M的坐标为(2,﹣1),试求点N的坐标;
(3)已知一个三角形各顶点坐标为D(0,6),E(﹣3,2),F(3,2),你能判定此三角形的形状吗?说明理由.
23.综合与实践
问题背景
如图,在平面直角坐标系中,点A的坐标为(﹣3,5),点B的坐标为(0,1),点C的坐标为(4,5),将线段AB沿AC方向平移,平移距离为线段AC的长度.
动手操作
(1)画出AB平移后的线段CD,直接写出B的对应点D的坐标;
探究证明
(2)连接BD,试探究∠BAC,∠BDC的数量关系,并证明你的结论;
拓展延伸
(3)若点E在线段BD上,连接AD,AE,且满足∠EAD=∠CAD,请求出∠ADB:∠AEB的值,并写出推理过程.
24.在平面直角坐标系中,D(0,﹣3)、M(4,﹣3).将一个直角三角形ABC放入平面直角坐标系中,∠ACB=90°.(不允许使用三角形内角和定理及其推论,否则记为零分)
(1)将直角三角形ABC,如图1位置摆放,边AC过O点,边AB与x轴、直线DM分别交于G、F,边BC与直线DM交于E,若∠AOG=60°,直接写出∠CED= ;
(2)如图1中的直角三角形ABC绕O点旋转到图2位置,N为线段OA上一点,∠NEC+∠CEF=180°,请写出∠NEF和∠AOG之间的数量关系,并说明理由;
(3)将直角三角形ABC如图3位置摆放,延长AC交DM于E,GE平分∠AED交x轴于点G,点B在直线DM上,BT平分∠HBC交EG于T,求∠GTB的值.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵点A(a,1)与点B (5,﹣1)关于x轴对称,
∴a=5,
故选:C.
2.解:∵A、B两点关于y轴对称,A的坐标是(2,﹣8),
∴点B的坐标是(﹣2,﹣8),
故选:D.
3.解:∵点P位于第二象限,
∴点的横坐标为负数,纵坐标为正数,
∵点距离x轴5个单位长度,距离y轴3个单位长度,
∴点的坐标为(﹣3,5).
故选:D.
4.解:点P(6,8)到原点的距离为:=10,故选:A.
5.解:∵点A(a,﹣b)在第三象限,
∴a<0,﹣b<0,
∴b>0,
∴﹣ab>0,
∴点B(﹣ab,b)所在的象限是第一象限.
故选:A.
6.解:∵AB∥x轴,点A的坐标为(2,1),
∴A、B两点纵坐标都是1,
又∵AB=3,
∴当B点在A点左边时,B的坐标为(﹣1,1),
当B点在A点右边时,B的坐标为(5,1).
故选:C.
7.解:根据题意,点Q的横坐标为:﹣2﹣3=﹣5;纵坐标为﹣3+2=﹣1;
即点Q的坐标是(﹣5,﹣1).
故选:C.
8.解:如图,过点B作BE⊥x轴于E,过点C作CF⊥x轴于F.
∵A(1,0),B(﹣2,4),
∴OA=1,BE=4,OE=2,AE=3,
∵∠AEB=∠AFC=∠BAC=90°,
∴∠B+∠BAE=90°,∠BAE+∠CAF=90°,
∴∠B=∠CAF,
∵AB=AC,
∴△BEA≌△AFC(AAS),
∴CF=AE=3,AF=BE=4,OF=1+4=5,
∴C(5,3),
故选:C.
9.解:∵点M(a+3,2a﹣4)在x轴上,
∴2a﹣4=0,
解得:a=2,
则a+3=5,
∴点M的坐标为:(5,0).
故选:B.
10.解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a,3)在第二象限,
∴a到直线m的距离为:2﹣a,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a,
故P点对称的点的坐标是:(﹣a+4,3).
故选:D.
二.填空题(共8小题,满分32分)
11.解:由于|m+5|+=0,
所以 m+5=0,n﹣3=0,
所以 m=﹣5,n=3,
所以 点P的坐标是(﹣5,3).
所以点P(m,n)关于x轴的对称点的坐标是 (﹣5,﹣3).
故答案是:(﹣5,﹣3).
12.解:∵A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,
∴a﹣5=0,b+3=0,
解得:a=5,b=﹣3,
∴C(a,b)的坐标为:(5,﹣3).
故答案为:(5,﹣3).
13.解:∵点(2,a)与点(b,﹣1)关于原点对称,
∴a=1,b=﹣2,
∴ab=﹣2.
故答案为:﹣2.
14.解:∵A(m﹣1,3),B (1,m2﹣1).AB∥x轴,
∴m2﹣1=3,
解得:m=±2;
当m=2时,A,B两点坐标都是(1,3),不符合题意,舍去,
∴m=﹣2;
故答案为:﹣2.
15.解:∵将点A(﹣1,2)先向左平移2个单位,横坐标﹣2,
再向上平移1个单位纵坐标+1,
∴平移后得到的点A1的坐标为:(﹣3,3).
故答案为:(﹣3,3).
16.解:∵点M(1﹣m,m+2)与点N(2m+3,m+2)的纵坐标都是m+2,
∴MN∥x轴,
点N在点M的左边时,1﹣m﹣(2m+3)=5,解得m=﹣,
点N在点M的右边时,2m+3﹣1+m=5,解得m=1,
综上所述,m的值是﹣或1.
故答案为:﹣或1.
17.解:作图如下,
∵∠MPO+∠POM=90°,∠QON+∠POM=90°,
∴∠MPO=∠QON,
在△PMO和△ONQ中,
,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
∵P点坐标为(4,6),
∴Q点坐标为(6,﹣4),
故答案为(6,﹣4).
18.解:如图所示:点C的坐标表示为(3,240°).
故答案为:(3,240°).
三.解答题(共6小题,满分48分)
19.解:(1)如图所示:△A1B1C1即为所求;
(2)A1(﹣2,﹣3),B1(0,1),C1(﹣3,0);
故答案为:﹣2,﹣3;0,1;﹣3,0.
(3)如图可得:
S△ABC=S长方形EFGB﹣S△BEC﹣S△CFA﹣S△AGB
=BE EF﹣EB CE﹣CF FA﹣AG BG
=3×4﹣×3×1﹣×3×1﹣×2×4
=5.
20.解:(1)∵点P在x轴上,
∴a+5=0,
∴a=﹣5,
∴2a﹣2=2×(﹣5)﹣2=﹣12,
∴点P的坐标为(﹣12,0).
(2)点Q的坐标为(4,5),直线PQ∥y轴,
∴2a﹣2=4,
∴a=3,
∴a+5=8,
∴点P的坐标为(4,8).
(3)∵点P在第二象限,且它到x轴、y轴的距离相等,
∴2a﹣2=﹣(a+5),
∴2a﹣2+a+5=0,
∴a=﹣1,
∴a2020+2020=(﹣1)2020+2020=2021.
∴a2020+2020的值为2021.
21.解:(1)如图,过点C作CE⊥OA于E.
∵A(6,0),
∵OA=OC=6,
∵∠COE=45°,
∴EC=OE=3,
∴C(3,3).
(2)如图,CD在x轴上方时,设CD交y轴于F,过点D作DT⊥x轴于T.
∵CD∥x轴,
∴CD⊥OF,
∵OB=OD=8,OC=OA=6,
∴CD===10,
∴DT=OF==,
∴OT===,CF=10﹣=,
∴C(,),
当CD在x轴下方时,同法可得C(﹣,﹣).
综上所述,满足条件的点C的坐标为(,)或(﹣,﹣).
22.解:(1)A,B两点间的距离==4;
(2)∵线段MN∥y轴,
∴M、N的横坐标相同,
设N(2,t),
∴|t+1|=4,解得t=3或﹣5,
∴N点坐标为(2,3)或(2,﹣5);
(3)△DEF为等腰三角形.
理由如下:
∵D(0,6),E(﹣3,2),F(3,2),
∴DE==5,DF==5,EF==6,
∴DE=DF,
∴△DEF为等腰三角形.
23.解:(1)如图,CD为所作,
因为AB向右平移7个单位,
所以D点坐标为(7,1);
(2)∠BAC=∠BDC.
理由如下:
∵AB平移后的线段CD,
∴AB∥CD,AC∥BD,
∴∠ABD+∠BDC=180°,∠BAC+∠ABD=180°,
∴∠BAC=∠BDC;
(3)∠ADB:∠AEB=1:2;
理由如下:∵AC∥BD,
∴∠CAD=∠ADB,∠AEB=∠CAE,
∵∠EAD=∠CAD,
∴∠CAE=2∠CAD,
∴∠AEB=2∠ADB,
即∠ADB:∠AEB=1:2.
24.解:(1)如图1,过C作CK∥x轴,则∠AOG=∠ACK=60°,
∵∠ACB=90°,
∴∠BCK=90°﹣60°=30°,
∵D(0,﹣3),M(4,﹣3)
∴DM∥x轴
∵CK∥x轴,
∴DM∥CK,
∴∠BCK=∠CED=30°,
故答案为:30°;
(2)∠NEF=2∠AOG,理由如下:
如图2,过点C作CK∥x轴,
∵D(0,﹣3),M(4,﹣3),
∴DM∥x轴,
∵CK∥x轴,
∴DM∥CK∥x轴,
∴∠AOG=∠ACK,
∵∠KCE+∠CEF=180°,∠NEC+∠CEF=180°,
∴∠KCE=∠NEC,
∵CK∥DM,
∴∠KCE=∠CEH,
∴∠NEC=∠CEH,
∵∠NEF=180°﹣∠NEC﹣∠CEH,
∴∠NEF=180°﹣2∠KCE,
∵∠AOG=∠ACK=90°﹣∠KCE,
∴∠NEF=2∠AOG;
(3)如图3,作TL∥MH,CK∥MH,
∵TL∥MH,CK∥MH,DM∥OG,
∴TL∥CK∥DM∥OG,
∵GE平分∠AED,BT平分∠HBC,
∴可设∠AEG=∠GEB=α,∠HBT=∠TBC=β,
可得∠AEB=2α,∠CBE=180°﹣2β,
∴∠ACB=180﹣2β+2α,
又∵∠ACB=90°,
∴180﹣2β+2α=90°,
∴β﹣α=45°,
∵TL∥MH,
∴∠GTL=∠GEB=α,∠BTL=180°﹣∠TBH=180°﹣β,
∴∠GTB=α+180°﹣β,
∴∠GTB=180°﹣(β﹣α)=135°.
