2021-2022学年高中数学必修上册课件:3.1.1 二次方程根的分布 课件(共14张ppt)
文档属性
| 名称 | 2021-2022学年高中数学必修上册课件:3.1.1 二次方程根的分布 课件(共14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 424.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
二次方程根的分布
2021-2022学年高中数学必修上册课件:
如果函数y=f(x)在区间[a,b]上的图象是连续
不断的一条曲线,并且有f(a)·f(b)<0,那么,函
数y=f(x)在区间(a,b) 内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
注:只要满足上述两个条件,就能判断函数在指定区间内存在零点.
复习旧知:零点存在性定理
引例
1.若关于x的方程ax2+bx+c=0()的两根一根大于0,一根小于0,则实数应满足条件是什么?
2.如果“一根大于1,一根小于1”呢?
一类:一元二次方程两根分布在两个不同区间内
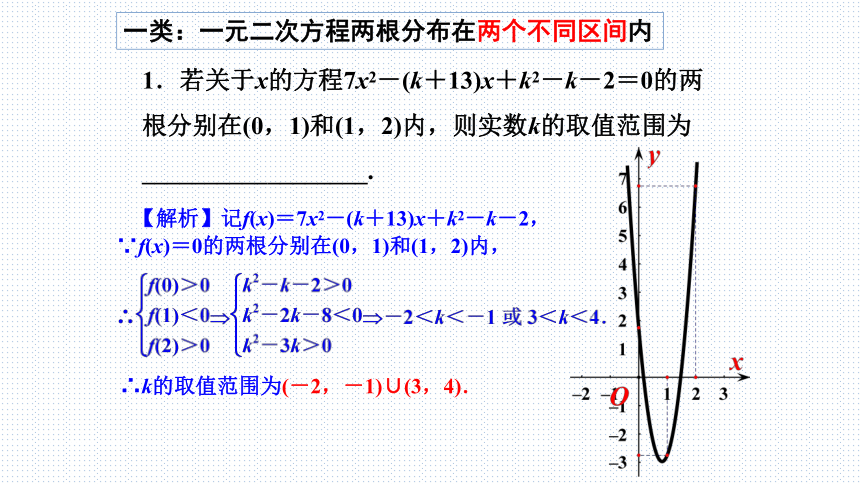
1.若关于x的方程7x2-(k+13)x+k2-k-2=0的两根分别在(0,1)和(1,2)内,则实数k的取值范围为__________________.
【解析】记f(x)=7x2-(k+13)x+k2-k-2,
∵f(x)=0的两根分别在(0,1)和(1,2)内,
∴k的取值范围为(-2,-1)∪(3,4).
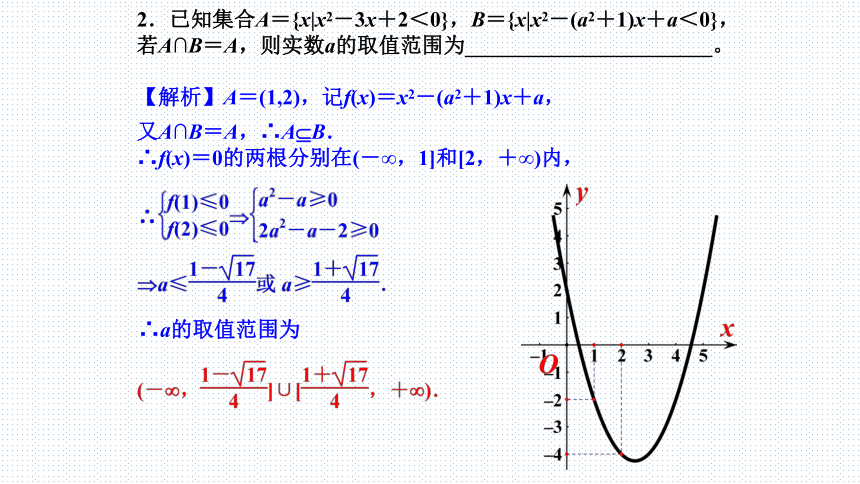
2.已知集合A={x|x2-3x+2<0},B={x|x2-(a2+1)x+a<0},若A∩B=A,则实数a的取值范围为_______________________。
【解析】A=(1,2),记f(x)=x2-(a2+1)x+a,
又A∩B=A,∴A B.
∴f(x)=0的两根分别在(-∞,1]和[2,+∞)内,
∴a的取值范围为
3.若关于x的不等式组 的整数解只
有-2,则实数k的取值范围为_____________。
4.若关于x的方程x2-mx-m+3=0在下列区间内有且只有一个根。
(1)(1,2),则实数m的取值范围为________________;
(2)[1,2],则实数m的取值范围为________________;
(3)(0,2),则实数m的取值范围为________________。
(2,)
(2,]
[,3)
小结:
一元二次方程两根分布在两个不同区间内的充要条件: 只需考虑方程对应函数在区间端点的符号即可.
二类:一元二次方程两根分布在同一个区间内
1.若关于x的方程x2+(a+1)x+1=0在区间(0,2)上
有两个根,则实数a的取值范围为___________.
(,3]
2.若关于x的方程x2+(2m-1)x+m2=0两个根都大于1,则实数m的取值范围为______________.
(,2)
3.已知A={x|x2+(p+2)x+p2=0},若A∩[-1,+∞)=Ф,
则实数p的取值范围为_____________________.
(,
4.若关于x的方程ax2+2x+1=0至少有一负实根,则实数a的取值范围为______________。
(,1]
小结:
一元二次方程两根分布在同一区间内的充要条件:必须同时考虑方程对应函数在区间端点的符号、方程根的判别式符号、对称轴在区间内.
二次方程根的分布
2021-2022学年高中数学必修上册课件:
如果函数y=f(x)在区间[a,b]上的图象是连续
不断的一条曲线,并且有f(a)·f(b)<0,那么,函
数y=f(x)在区间(a,b) 内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
注:只要满足上述两个条件,就能判断函数在指定区间内存在零点.
复习旧知:零点存在性定理
引例
1.若关于x的方程ax2+bx+c=0()的两根一根大于0,一根小于0,则实数应满足条件是什么?
2.如果“一根大于1,一根小于1”呢?
一类:一元二次方程两根分布在两个不同区间内
1.若关于x的方程7x2-(k+13)x+k2-k-2=0的两根分别在(0,1)和(1,2)内,则实数k的取值范围为__________________.
【解析】记f(x)=7x2-(k+13)x+k2-k-2,
∵f(x)=0的两根分别在(0,1)和(1,2)内,
∴k的取值范围为(-2,-1)∪(3,4).
2.已知集合A={x|x2-3x+2<0},B={x|x2-(a2+1)x+a<0},若A∩B=A,则实数a的取值范围为_______________________。
【解析】A=(1,2),记f(x)=x2-(a2+1)x+a,
又A∩B=A,∴A B.
∴f(x)=0的两根分别在(-∞,1]和[2,+∞)内,
∴a的取值范围为
3.若关于x的不等式组 的整数解只
有-2,则实数k的取值范围为_____________。
4.若关于x的方程x2-mx-m+3=0在下列区间内有且只有一个根。
(1)(1,2),则实数m的取值范围为________________;
(2)[1,2],则实数m的取值范围为________________;
(3)(0,2),则实数m的取值范围为________________。
(2,)
(2,]
[,3)
小结:
一元二次方程两根分布在两个不同区间内的充要条件: 只需考虑方程对应函数在区间端点的符号即可.
二类:一元二次方程两根分布在同一个区间内
1.若关于x的方程x2+(a+1)x+1=0在区间(0,2)上
有两个根,则实数a的取值范围为___________.
(,3]
2.若关于x的方程x2+(2m-1)x+m2=0两个根都大于1,则实数m的取值范围为______________.
(,2)
3.已知A={x|x2+(p+2)x+p2=0},若A∩[-1,+∞)=Ф,
则实数p的取值范围为_____________________.
(,
4.若关于x的方程ax2+2x+1=0至少有一负实根,则实数a的取值范围为______________。
(,1]
小结:
一元二次方程两根分布在同一区间内的充要条件:必须同时考虑方程对应函数在区间端点的符号、方程根的判别式符号、对称轴在区间内.
