人教版数学七年级上册_4.3.3余角和补角教学PPT(共17张)
文档属性
| 名称 | 人教版数学七年级上册_4.3.3余角和补角教学PPT(共17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 801.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
余角和补角
1、在一副三角尺中,每一块都有一个角是90°,
那么其余两个角的和是多少度?
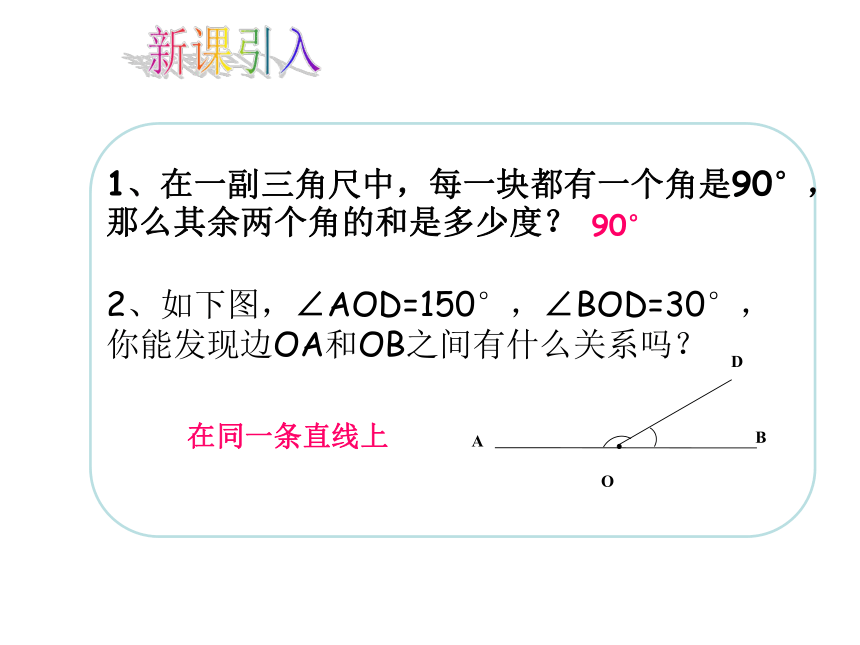
2、如下图,∠AOD=150°,∠BOD=30°,
你能发现边OA和OB之间有什么关系吗?
A
O
B
D
90°
在同一条直线上
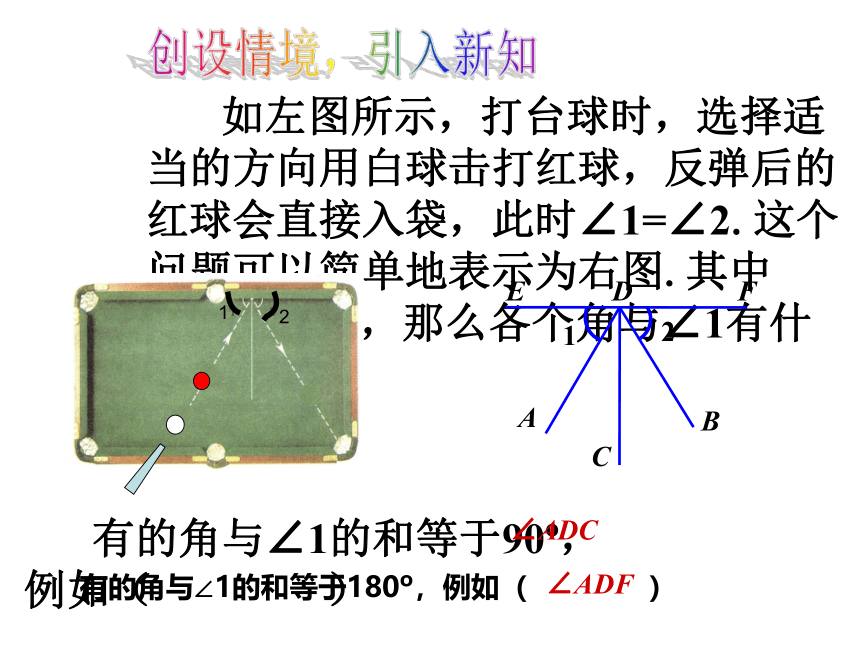
如左图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为右图.其中∠EDC=90 ,那么各个角与∠1有什么关系?
1
2
A
C
B
E
D
F
1
2
有的角与∠1的和等于90 ,例如( )
∠ADC
有的角与∠1的和等于180 ,例如( )
∠ADF
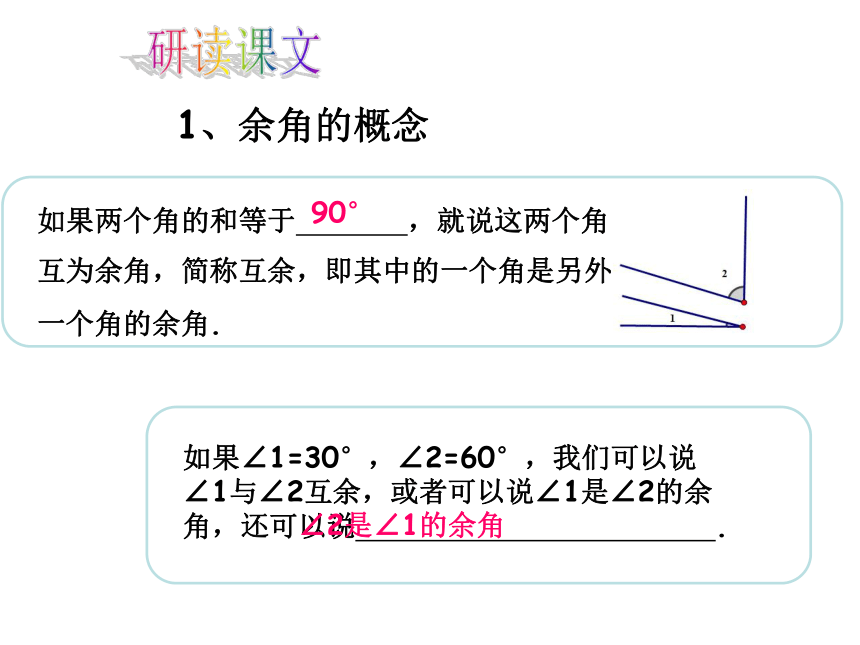
1、余角的概念
如果两个角的和等于 ,就说这两个角
互为余角,简称互余,即其中的一个角是另外
一个角的余角.
如果∠1=30°,∠2=60°,我们可以说∠1与∠2互余,或者可以说∠1是∠2的余角,还可以说 .
90°
∠2是∠1的余角
如果两个角的和等于 ,就说这两个
角互为补角,简称互补,即其中的一个角
是另外一个角的补角.
2、补角的概念
如果∠1=45°,∠2=135°,我们可以说∠1与∠2互补,或者可以说∠1是∠2的补角,还可以说 .
180°
∠2是∠1的补角
练一练
∠1和∠4;
∠2和∠3
∠1和∠8;
∠2和∠5;
∠3和∠6;
∠4和∠5;
1、∠1=10°,∠2=30°,∠3=60°,∠4=80°, ∠5=100°,∠6=120°,∠7=150°,∠8=170°,
其中互为余角的有: ;
互为补角的有: .
由此,我们可以得到补角性质:
类似地,余角的性质:
.
补角和余角的性质
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,求证:∠2=∠4
证明:∵∠1与∠2互补
∴∠2=180°-
∵∠3与∠4互补
∴∠4=180°-
∵∠1=∠3
∴180°-∠1=180°-∠3
∴∠2=∠4 ( )
2
1
3
4
∠1
∠3
同角(等角)的补角相等
同角(等角)的余角相等
等量代换
例3 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
所以∠COD +∠COE= ∠AOC+ ∠BOC
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
= (∠AOC+ ∠BOC)
=90°
所以, ∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,
∠COD 和∠BOE也互为余角.
方位角的概念
在生活当中,我们有时候需要用到角来描述方位,我们把这样的角称为方位角.方位角有时以 为基准,描述物体运动的方向.
正北或正南方向
方位角的表示习惯上以正北、正南方向为基准来描述物体的方向.即用“北偏东多少度”“北偏西多少度”或者“南偏东多少度”“南偏西多少度”来表示方向.
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上,同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
40°
B
C
10°
45°
D
画法 以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
1、一个角的余角比它大20°,则这个角是____.
35°
2、按照上北下南,左西右东的规定画出表示东南西北的十字线,然后在图上表示下列方向的射线:
(1)北偏东30° (2)南偏东15°
30°
15°
1、如果两个角的和等于90°,就说这两个角互为余角,简称_____,即其中的一个角是另外一个角的_____.
2、如果两个角的和等于180°,就说这两个角互为补角,简称_____,即其中的一个角是另外一个角的_____
3、同角(等角)的_____相等,
同角(等角)的_____相等.
4、学习反思:
互补
互余
余角
补角
补角
余角
成功=艰苦劳动+正确的方法+少说空话.
———— 爱因斯坦
余角和补角
1、在一副三角尺中,每一块都有一个角是90°,
那么其余两个角的和是多少度?
2、如下图,∠AOD=150°,∠BOD=30°,
你能发现边OA和OB之间有什么关系吗?
A
O
B
D
90°
在同一条直线上
如左图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为右图.其中∠EDC=90 ,那么各个角与∠1有什么关系?
1
2
A
C
B
E
D
F
1
2
有的角与∠1的和等于90 ,例如( )
∠ADC
有的角与∠1的和等于180 ,例如( )
∠ADF
1、余角的概念
如果两个角的和等于 ,就说这两个角
互为余角,简称互余,即其中的一个角是另外
一个角的余角.
如果∠1=30°,∠2=60°,我们可以说∠1与∠2互余,或者可以说∠1是∠2的余角,还可以说 .
90°
∠2是∠1的余角
如果两个角的和等于 ,就说这两个
角互为补角,简称互补,即其中的一个角
是另外一个角的补角.
2、补角的概念
如果∠1=45°,∠2=135°,我们可以说∠1与∠2互补,或者可以说∠1是∠2的补角,还可以说 .
180°
∠2是∠1的补角
练一练
∠1和∠4;
∠2和∠3
∠1和∠8;
∠2和∠5;
∠3和∠6;
∠4和∠5;
1、∠1=10°,∠2=30°,∠3=60°,∠4=80°, ∠5=100°,∠6=120°,∠7=150°,∠8=170°,
其中互为余角的有: ;
互为补角的有: .
由此,我们可以得到补角性质:
类似地,余角的性质:
.
补角和余角的性质
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,求证:∠2=∠4
证明:∵∠1与∠2互补
∴∠2=180°-
∵∠3与∠4互补
∴∠4=180°-
∵∠1=∠3
∴180°-∠1=180°-∠3
∴∠2=∠4 ( )
2
1
3
4
∠1
∠3
同角(等角)的补角相等
同角(等角)的余角相等
等量代换
例3 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
所以∠COD +∠COE= ∠AOC+ ∠BOC
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
= (∠AOC+ ∠BOC)
=90°
所以, ∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,
∠COD 和∠BOE也互为余角.
方位角的概念
在生活当中,我们有时候需要用到角来描述方位,我们把这样的角称为方位角.方位角有时以 为基准,描述物体运动的方向.
正北或正南方向
方位角的表示习惯上以正北、正南方向为基准来描述物体的方向.即用“北偏东多少度”“北偏西多少度”或者“南偏东多少度”“南偏西多少度”来表示方向.
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上,同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
40°
B
C
10°
45°
D
画法 以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
1、一个角的余角比它大20°,则这个角是____.
35°
2、按照上北下南,左西右东的规定画出表示东南西北的十字线,然后在图上表示下列方向的射线:
(1)北偏东30° (2)南偏东15°
30°
15°
1、如果两个角的和等于90°,就说这两个角互为余角,简称_____,即其中的一个角是另外一个角的_____.
2、如果两个角的和等于180°,就说这两个角互为补角,简称_____,即其中的一个角是另外一个角的_____
3、同角(等角)的_____相等,
同角(等角)的_____相等.
4、学习反思:
互补
互余
余角
补角
补角
余角
成功=艰苦劳动+正确的方法+少说空话.
———— 爱因斯坦
