人教版数学七年级上册4.1 几何图形练习(word版、含解析)
文档属性
| 名称 | 人教版数学七年级上册4.1 几何图形练习(word版、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 107.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 21:14:12 | ||
图片预览

文档简介
4.1 几何图形
一 、单选题(本大题共15小题,共45分)
1一个棱柱体有条棱,这是一个
A. 六棱柱 B. 七棱柱 C. 八棱柱 D. 九棱柱
2如图是一个正方体包装盒的表面展开图,若在其中的三个面,,上分别填上适当的数,使得,,的数字与其对面数字互为相反数,则,,上数字分别为
A. ,, B. ,, C. ,, D. ,,
3如图,正方体的个面上分别标有字母,,,,,,将该正方体按图示方式转动,根据图形可得,与字母相对的是
A. 字母 B. 字母 C. 字母 D. 字母
4如图,是一个正方体纸盒的展开图,若在其中的三个正方形,,内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形内的三个数依次为
A. ,, B. ,, C. ,, D. ,,
5如图,直角三角形绕直线旋转一周,得到的立体图形是
A. B. C. D.
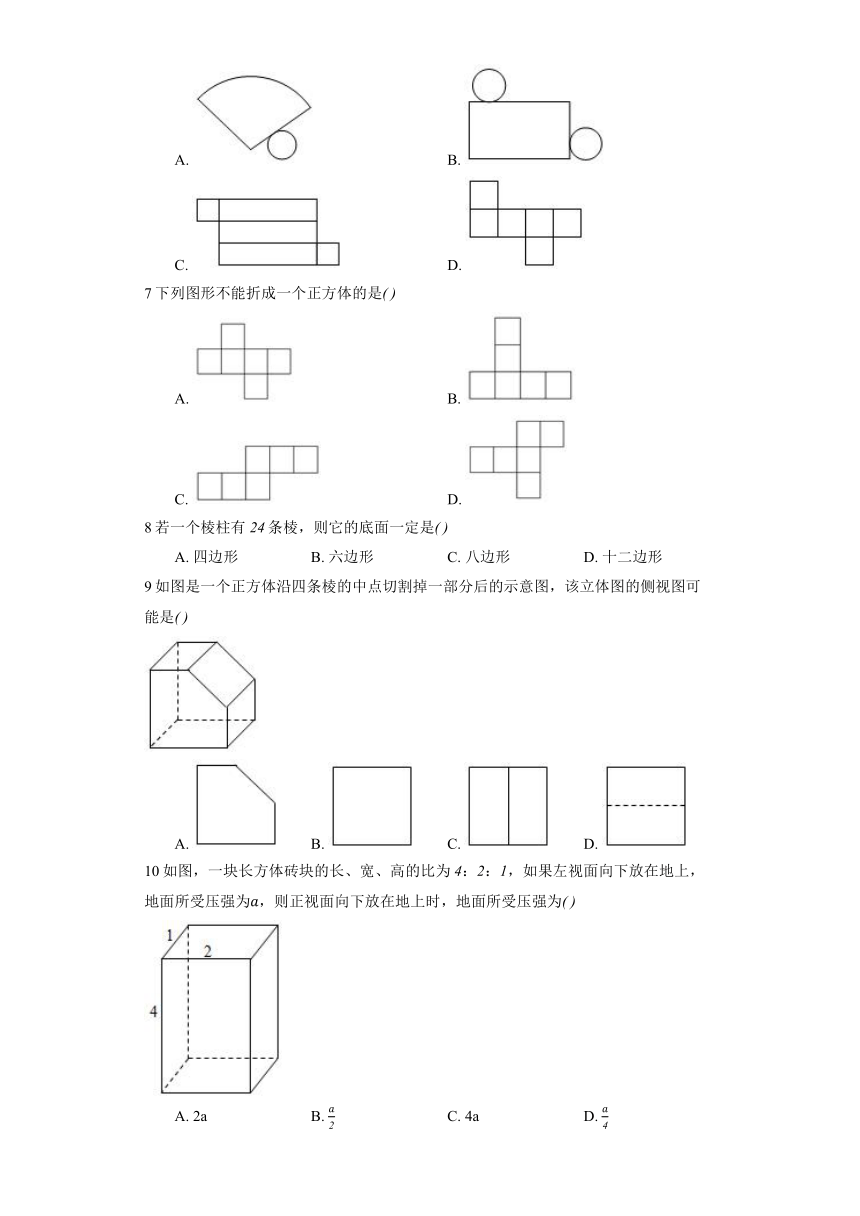
6以下平面图形按某种方式折叠后,能够围成立体图形的是
A. B.
C. D.
7下列图形不能折成一个正方体的是
A. B.
C. D.
8若一个棱柱有条棱,则它的底面一定是
A. 四边形 B. 六边形 C. 八边形 D. 十二边形
9如图是一个正方体沿四条棱的中点切割掉一部分后的示意图,该立体图的侧视图可能是
A. B. C. D.
10如图,一块长方体砖块的长、宽、高的比为::,如果左视面向下放在地上,地面所受压强为,则正视面向下放在地上时,地面所受压强为
A. B. C. D.
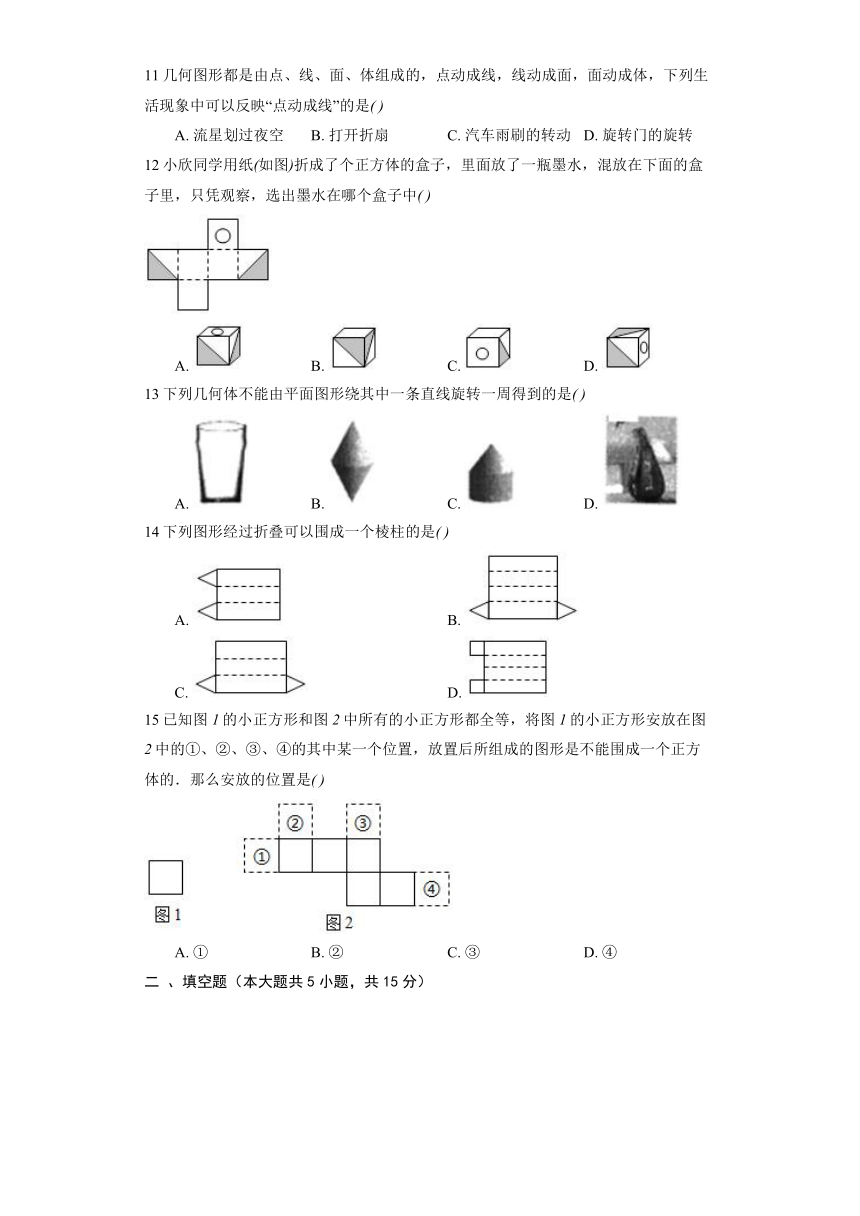
11几何图形都是由点、线、面、体组成的,点动成线,线动成面,面动成体,下列生活现象中可以反映“点动成线”的是
A. 流星划过夜空 B. 打开折扇 C. 汽车雨刷的转动 D. 旋转门的旋转
12小欣同学用纸如图折成了个正方体的盒子,里面放了一瓶墨水,混放在下面的盒子里,只凭观察,选出墨水在哪个盒子中
A. B. C. D.
13下列几何体不能由平面图形绕其中一条直线旋转一周得到的是
A. B. C. D.
14下列图形经过折叠可以围成一个棱柱的是
A. B.
C. D.
15已知图的小正方形和图中所有的小正方形都全等,将图的小正方形安放在图中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是
A. ① B. ② C. ③ D. ④
二 、填空题(本大题共5小题,共15分)
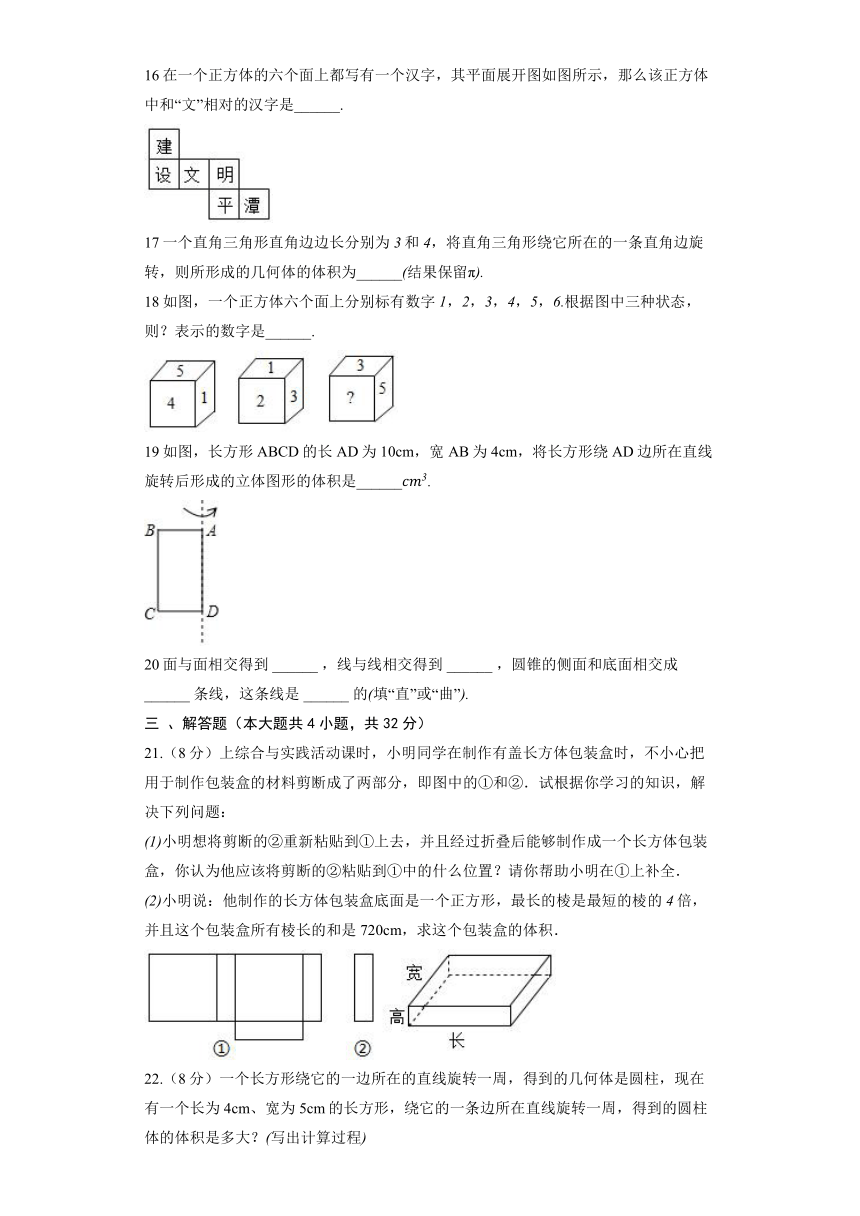
16在一个正方体的六个面上都写有一个汉字,其平面展开图如图所示,那么该正方体中和“文”相对的汉字是______.
17一个直角三角形直角边边长分别为和,将直角三角形绕它所在的一条直角边旋转,则所形成的几何体的体积为______结果保留
18如图,一个正方体六个面上分别标有数字,,,,,根据图中三种状态,则?表示的数字是______.
19如图,长方形的长为,宽为,将长方形绕边所在直线旋转后形成的立体图形的体积是______
20面与面相交得到 ______ ,线与线相交得到 ______ ,圆锥的侧面和底面相交成 ______ 条线,这条线是 ______ 的填“直”或“曲”
三 、解答题(本大题共4小题,共32分)
21.(8分)上综合与实践活动课时,小明同学在制作有盖长方体包装盒时,不小心把用于制作包装盒的材料剪断成了两部分,即图中的①和②.试根据你学习的知识,解决下列问题:
小明想将剪断的②重新粘贴到①上去,并且经过折叠后能够制作成一个长方体包装盒,你认为他应该将剪断的②粘贴到①中的什么位置?请你帮助小明在①上补全.
小明说:他制作的长方体包装盒底面是一个正方形,最长的棱是最短的棱的倍,并且这个包装盒所有棱长的和是,求这个包装盒的体积.
22.(8分)一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为、宽为的长方形,绕它的一条边所在直线旋转一周,得到的圆柱体的体积是多大?写出计算过程
23.(8分)一块长、宽、高分别为、、的长方体橡皮泥,要用它来捏一个底面半径为的圆柱,圆柱的高是多少厘米?精确到,取.
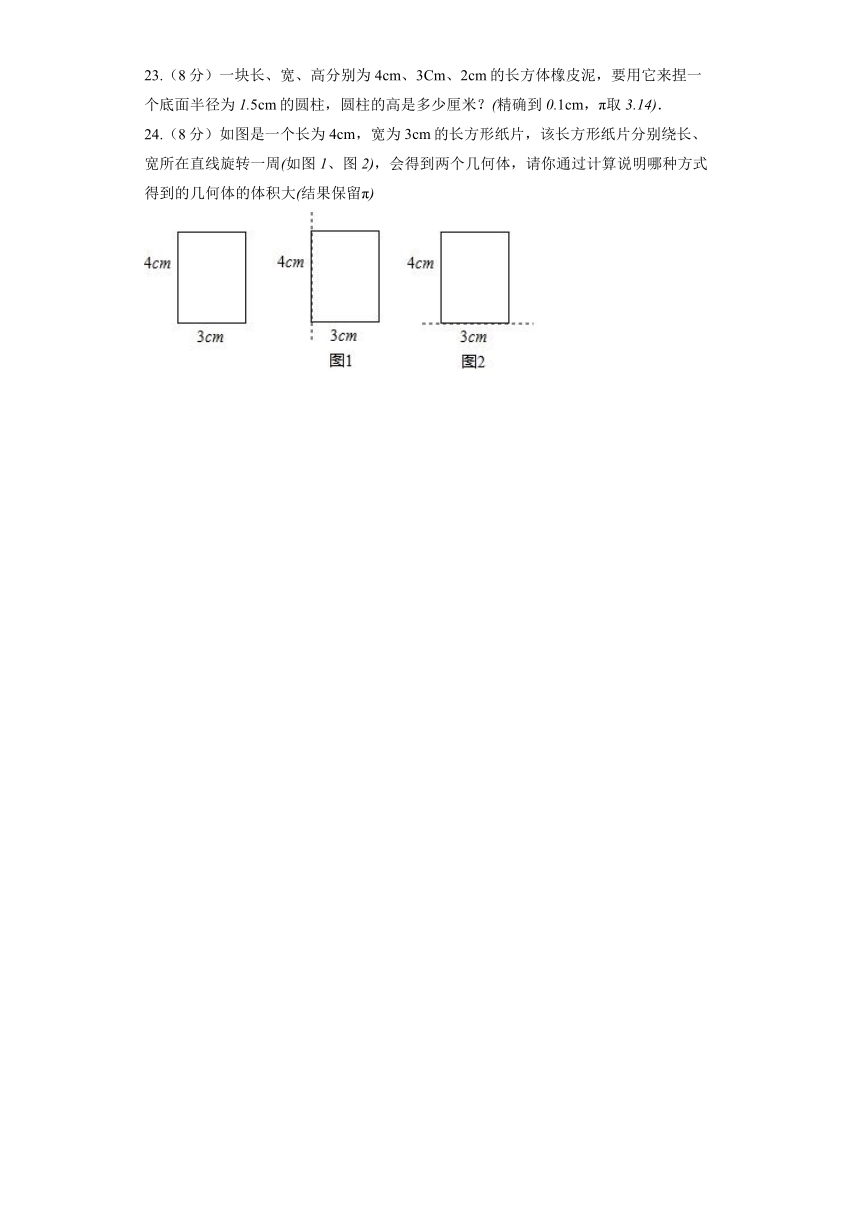
24.(8分)如图是一个长为,宽为的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周如图、图,会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大结果保留
答案和解析
1.【答案】A;
【解析】解:由棱柱有条棱可得,
一个棱柱体有条棱,,因此这个棱柱是六棱柱,
故选:
由棱柱的形体特征进行判断即可.
此题主要考查认识立体图形,掌握棱柱的形体特征是正确判断的关键.
2.【答案】A;
【解析】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“”与“”是相对面,
“”与“”是相对面,
“”与“”是相对面,
相对面上的两数互为相反数,
、、内的三个数依次是、、
故选:
依据对面不存任何公共部分可确定出对面,然后依据相反数的定义解答即可.
此题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
3.【答案】C;
【解析】解:由此正方体的不同放置可知:与字母相对的是字母
故选:
由此正方体的不同放置可知:与相对,相对的是,由此得出答案.
本题正方体相对两个面上的文字,同时也考查了空间想象能力和推理能力,属于基础题.
4.【答案】A;
【解析】解:由图可知对应,对应,对应
的相反数为,的相反数为,的相反数为,
,,
故选:
本题可根据图形的折叠性,对图形进行分析,可知对应,对应,对应两数互为相反数,和为,据此可解此题.
此题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
5.【答案】D;
【解析】解:直角三角形绕直线旋转一周,得到的立体图形是圆锥体,
故选:
根据面动成体进行判断即可.
此题主要考查点、线、面、体,理解点动成线,线动成面,面动成体是正确判断的前提.
6.【答案】D;
【解析】解:、无法围成立体图形,不合题意;
、无法围成立体图形,不合题意;
、无法围成立体图形,不合题意;
、可以围成立方体,符合题意.
故选:
直接利用常见几何体与展开图的关系得出答案.
此题主要考查了展开图折叠成几何体,正确掌握基本图形与几何体的关系是解题关键.
7.【答案】B;
【解析】解:正方体展开图共有大类,种情况,由此可知选项图形不在个之内,因此不能折成一个正方体,
故选:
根据正方体展开图的种特征,图属于正方体展开图的“”型,能折成正方体;图属于正方体展开图的“”型,能折成正方体;图属于正方体展开图的“”型,能折成正方体;图不属于正方体展开图,不能折成正方体.据此解答.
此题主要考查了展开图折叠成几何体,正方体展开图有种特征,分四种类型,即:第一种:“”结构,即第一行放个,第二行放个,第三行放个;第二种:“”结构,即每一行放个正方形,此种结构只有一种展开图;第三种:“”结构,即每一行放个正方形,只有一种展开图;第四种:“”结构,即第一行放个正方形,第二行放个正方形,第三行放个正方形.
8.【答案】C;
【解析】解:棱柱有条棱,又,因此底面是八边形,
故选:
根据棱柱中棱的条数为,由棱的总条数为,可求出答案.
此题主要考查认识立体图形,掌握棱柱的顶点、面数和棱的条数是正确判断前提.
9.【答案】D;
【解析】解:从侧面看该几何体,选项中的图形符合题意,
故选:
根据简单几何体的三视图的画法,看得见的轮廓线用实线表示,看不见的轮廓线用虚线表示可得答案.
此题主要考查简单几何体的三视图,理解视图的意义是正确判断的前提,掌握看得见的轮廓线用实线表示,看不见的轮廓线用虚线表示是得出正确答案的关键.
10.【答案】B;
【解析】解:设长方体砖块的长、宽、高分别为,,,
则左视图的面积为,主视图的面积为,
因此主视图的面积是左视图面积的倍,
所以主视图在下所受到的压强是左视图向下所受压强的,即,
故选:
求出主视图和左视图面积之间的倍比关系,再根据在压力一定时,压强与受力面积成反比,得出答案.
此题主要考查认识立体图形,求出主视图和左视图面积之间的倍比关系是正确解答的前提,理解压强与受力面积的关系是解决问题的关键.
11.【答案】A;
【解析】解:、流星划过夜空,属于点动成线,本选项符合题意.
、打开折扇,属于线动成面,本选项不符合题意.
、汽车雨刷的转动,属于线动成面,本选项不符合题意.
、旋转门的旋转,属于面动成体,本选项不符合题意,
故选:
根据从运动的观点来看点动成线,线动成面,面动成体可得答案.
此题主要考查了点、线、面、体,关键是掌握四者之间的关系.
12.【答案】B;
【解析】解:根据展开图中各种符号的特征和位置,可得墨水在盒子里面.
故选:
在验证立方体的展开图时,要细心观察每一个标志的位置是否一致,然后进行判断.
此题主要考查正方体的表面展开图及空间想象能力.易错易混点:学生对相关图的位置想象不准确,从而错选,解决这类问题时,不妨动手实际操作一下,即可解决问题.
13.【答案】D;
【解析】解:根据各个选项中的几何体的形体特征可知,选项中的几何体不能绕其中一条直线旋转一周得到,
故选:
根据“面动成体”进行判断即可.
此题主要考查“面动成体”,理解点、线、面、体的意义以及相互关系是正确判断的关键.
14.【答案】C;
【解析】解:、不能围成棱柱,底面应该在两侧,故此选项不符合题意;
、不能围成棱柱,侧面有个,底面是三角形,应该是四边形才行,故此选项不符合题意;
、能围成三棱柱,侧面有个,底面是三角形,故此选项符合题意;
、不能围成棱柱,底面应该在两侧,故此选项不符合题意;
故选:
根据棱柱的特点进行分析即可.
此题主要考查了展开图折叠成几何体,关键是通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开.
15.【答案】A;
【解析】解:将图的正方形放在图中的①的位置出现重叠的面,所以不能围成正方体.
故选:
由平面图形的折叠及正方体的表面展开图的特点解题.
此题主要考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.
16.【答案】潭;
【解析】解:由正方体表面展开图的“相间、端是对面”可知,
“建”与“平”是相对的面,
“设”与“明”是相对的面,
“文”与“潭”是相对的面,
故答案为:潭.
根据正方体的表面展开图的特征进行判断即可.
此题主要考查正方体的展开与折叠,掌握正方体的表面展开图的特征是正确判断的前提.
17.【答案】16π或12π;
【解析】解:①以的直角边为轴旋转,可得到,底面半径为,高为的圆锥体,
因此体积为,
②以的直角边为轴旋转,可得到,底面半径为,高为的圆锥体,
因此体积为,
故答案为:或
分两种情况,分别利用圆锥体体积的计算方法进行计算即可.
此题主要考查点、线、面、体,掌握圆锥体体积的计算方法是得出正确答案的前提.
18.【答案】6;
【解析】解:由图一、二可得:标的与标,,,的面相邻,所以与相对;
由图二、三可得标的与标,,,的面相邻,所以与相对;
由图一、三可得标的与标,,的面相邻,所以与相对;
故既与又与相邻的是或,在上在右就是,在上在右就是所以此题答案是
故答案为:
利用正方体及其表面展开图的特点解题.
此题主要考查正方体相对两个面的文字问题,通过三个正方体中能看到的数字推出三组相对的数字是完成本题的关键.
19.【答案】160π;
【解析】解:由题意得,旋转后是底面半径为,高为的圆柱体,
因此体积为,
故答案为:
根据圆柱体体积的计算方法进行计算即可.
此题主要考查点、线、面、体,掌握圆柱体体积的计算方法是得出正确答案的前提.
20.【答案】线 点 一 曲;
【解析】解:面与面相交得到线,线与线相交得到点,圆锥的侧面和底面相交成一条线,这条线是曲的,
故答案为:线;点;一;曲.
根据点、线、面、体的概念以及圆锥的形状特点解答.
此题主要考查圆锥的知识,掌握圆锥的形状特点是解答该题的关键.
21.【答案】解:(1)如图,四种情况.
(2)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为a cm,则长与宽相等为4a cm,
∵长方体纸盒所有棱长的和是720cm,
∴4(a+4a+4a)=720,解得a=20cm,
∴这个长方体纸盒的体积为:20×80×80=128000(立方厘米).;
【解析】
根据长方体的展开图的情况可知有四种情况;
设最短的棱长高为,则长与宽相等为,根据棱长的和是,列出方程可求出长宽高,即可求出长方体纸盒的体积.
此题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
22.【答案】解:①以长为4cm的边所在的直线为轴,旋转一周可得到一个底面半径为5cm,高为4cm的圆柱体,
因此,体积为π×52×4=100π(c),
②以宽为4cm的边所在的直线为轴,旋转一周可得到一个底面半径为4cm,高为5cm的圆柱体,
因此,体积为π×42×5=80π(c),
答:绕它的一条边所在直线旋转一周,得到的圆柱体的体积为100πc或80πc.;
【解析】
以不同的边所在的直线为轴,可以得到两个不同的圆柱体,分两种情况依据圆柱体的体积的计算方法进行解答即可.
此题主要考查点、线、面、体,掌握圆柱体体积的计算方法是正确解答的前提.
23.【答案】解:设圆柱的高是hcm,根据题意得:
π×1.52h=4×3×2,
∴h≈3.4,
答:圆柱的高约是3.4cm.;
【解析】
直接利用圆柱体体积公式计算得出答案.
此题主要考查了认识立体图形,正确掌握圆柱体体积公式是解题关键.
24.【答案】解:如图,绕长旋转得到的圆柱的底面半径为,高为,体积;
如图,绕宽旋转得到的圆柱底面半径为,高为,体积.
因此绕宽旋转得到的圆柱体积大.;
【解析】绕长旋转得到的圆柱的底面半径为,高为,从而计算体积即可;绕宽旋转得到的圆柱底面半径为,高为,从而计算体积进行比较即可.
该题考查了点、线、面、体的知识,熟记常见平面图形旋转可得到什么立体图形是解决本题的关键,另外要掌握圆柱的体积计算公式.
一 、单选题(本大题共15小题,共45分)
1一个棱柱体有条棱,这是一个
A. 六棱柱 B. 七棱柱 C. 八棱柱 D. 九棱柱
2如图是一个正方体包装盒的表面展开图,若在其中的三个面,,上分别填上适当的数,使得,,的数字与其对面数字互为相反数,则,,上数字分别为
A. ,, B. ,, C. ,, D. ,,
3如图,正方体的个面上分别标有字母,,,,,,将该正方体按图示方式转动,根据图形可得,与字母相对的是
A. 字母 B. 字母 C. 字母 D. 字母
4如图,是一个正方体纸盒的展开图,若在其中的三个正方形,,内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形内的三个数依次为
A. ,, B. ,, C. ,, D. ,,
5如图,直角三角形绕直线旋转一周,得到的立体图形是
A. B. C. D.
6以下平面图形按某种方式折叠后,能够围成立体图形的是
A. B.
C. D.
7下列图形不能折成一个正方体的是
A. B.
C. D.
8若一个棱柱有条棱,则它的底面一定是
A. 四边形 B. 六边形 C. 八边形 D. 十二边形
9如图是一个正方体沿四条棱的中点切割掉一部分后的示意图,该立体图的侧视图可能是
A. B. C. D.
10如图,一块长方体砖块的长、宽、高的比为::,如果左视面向下放在地上,地面所受压强为,则正视面向下放在地上时,地面所受压强为
A. B. C. D.
11几何图形都是由点、线、面、体组成的,点动成线,线动成面,面动成体,下列生活现象中可以反映“点动成线”的是
A. 流星划过夜空 B. 打开折扇 C. 汽车雨刷的转动 D. 旋转门的旋转
12小欣同学用纸如图折成了个正方体的盒子,里面放了一瓶墨水,混放在下面的盒子里,只凭观察,选出墨水在哪个盒子中
A. B. C. D.
13下列几何体不能由平面图形绕其中一条直线旋转一周得到的是
A. B. C. D.
14下列图形经过折叠可以围成一个棱柱的是
A. B.
C. D.
15已知图的小正方形和图中所有的小正方形都全等,将图的小正方形安放在图中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是
A. ① B. ② C. ③ D. ④
二 、填空题(本大题共5小题,共15分)
16在一个正方体的六个面上都写有一个汉字,其平面展开图如图所示,那么该正方体中和“文”相对的汉字是______.
17一个直角三角形直角边边长分别为和,将直角三角形绕它所在的一条直角边旋转,则所形成的几何体的体积为______结果保留
18如图,一个正方体六个面上分别标有数字,,,,,根据图中三种状态,则?表示的数字是______.
19如图,长方形的长为,宽为,将长方形绕边所在直线旋转后形成的立体图形的体积是______
20面与面相交得到 ______ ,线与线相交得到 ______ ,圆锥的侧面和底面相交成 ______ 条线,这条线是 ______ 的填“直”或“曲”
三 、解答题(本大题共4小题,共32分)
21.(8分)上综合与实践活动课时,小明同学在制作有盖长方体包装盒时,不小心把用于制作包装盒的材料剪断成了两部分,即图中的①和②.试根据你学习的知识,解决下列问题:
小明想将剪断的②重新粘贴到①上去,并且经过折叠后能够制作成一个长方体包装盒,你认为他应该将剪断的②粘贴到①中的什么位置?请你帮助小明在①上补全.
小明说:他制作的长方体包装盒底面是一个正方形,最长的棱是最短的棱的倍,并且这个包装盒所有棱长的和是,求这个包装盒的体积.
22.(8分)一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为、宽为的长方形,绕它的一条边所在直线旋转一周,得到的圆柱体的体积是多大?写出计算过程
23.(8分)一块长、宽、高分别为、、的长方体橡皮泥,要用它来捏一个底面半径为的圆柱,圆柱的高是多少厘米?精确到,取.
24.(8分)如图是一个长为,宽为的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周如图、图,会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大结果保留
答案和解析
1.【答案】A;
【解析】解:由棱柱有条棱可得,
一个棱柱体有条棱,,因此这个棱柱是六棱柱,
故选:
由棱柱的形体特征进行判断即可.
此题主要考查认识立体图形,掌握棱柱的形体特征是正确判断的关键.
2.【答案】A;
【解析】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“”与“”是相对面,
“”与“”是相对面,
“”与“”是相对面,
相对面上的两数互为相反数,
、、内的三个数依次是、、
故选:
依据对面不存任何公共部分可确定出对面,然后依据相反数的定义解答即可.
此题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
3.【答案】C;
【解析】解:由此正方体的不同放置可知:与字母相对的是字母
故选:
由此正方体的不同放置可知:与相对,相对的是,由此得出答案.
本题正方体相对两个面上的文字,同时也考查了空间想象能力和推理能力,属于基础题.
4.【答案】A;
【解析】解:由图可知对应,对应,对应
的相反数为,的相反数为,的相反数为,
,,
故选:
本题可根据图形的折叠性,对图形进行分析,可知对应,对应,对应两数互为相反数,和为,据此可解此题.
此题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
5.【答案】D;
【解析】解:直角三角形绕直线旋转一周,得到的立体图形是圆锥体,
故选:
根据面动成体进行判断即可.
此题主要考查点、线、面、体,理解点动成线,线动成面,面动成体是正确判断的前提.
6.【答案】D;
【解析】解:、无法围成立体图形,不合题意;
、无法围成立体图形,不合题意;
、无法围成立体图形,不合题意;
、可以围成立方体,符合题意.
故选:
直接利用常见几何体与展开图的关系得出答案.
此题主要考查了展开图折叠成几何体,正确掌握基本图形与几何体的关系是解题关键.
7.【答案】B;
【解析】解:正方体展开图共有大类,种情况,由此可知选项图形不在个之内,因此不能折成一个正方体,
故选:
根据正方体展开图的种特征,图属于正方体展开图的“”型,能折成正方体;图属于正方体展开图的“”型,能折成正方体;图属于正方体展开图的“”型,能折成正方体;图不属于正方体展开图,不能折成正方体.据此解答.
此题主要考查了展开图折叠成几何体,正方体展开图有种特征,分四种类型,即:第一种:“”结构,即第一行放个,第二行放个,第三行放个;第二种:“”结构,即每一行放个正方形,此种结构只有一种展开图;第三种:“”结构,即每一行放个正方形,只有一种展开图;第四种:“”结构,即第一行放个正方形,第二行放个正方形,第三行放个正方形.
8.【答案】C;
【解析】解:棱柱有条棱,又,因此底面是八边形,
故选:
根据棱柱中棱的条数为,由棱的总条数为,可求出答案.
此题主要考查认识立体图形,掌握棱柱的顶点、面数和棱的条数是正确判断前提.
9.【答案】D;
【解析】解:从侧面看该几何体,选项中的图形符合题意,
故选:
根据简单几何体的三视图的画法,看得见的轮廓线用实线表示,看不见的轮廓线用虚线表示可得答案.
此题主要考查简单几何体的三视图,理解视图的意义是正确判断的前提,掌握看得见的轮廓线用实线表示,看不见的轮廓线用虚线表示是得出正确答案的关键.
10.【答案】B;
【解析】解:设长方体砖块的长、宽、高分别为,,,
则左视图的面积为,主视图的面积为,
因此主视图的面积是左视图面积的倍,
所以主视图在下所受到的压强是左视图向下所受压强的,即,
故选:
求出主视图和左视图面积之间的倍比关系,再根据在压力一定时,压强与受力面积成反比,得出答案.
此题主要考查认识立体图形,求出主视图和左视图面积之间的倍比关系是正确解答的前提,理解压强与受力面积的关系是解决问题的关键.
11.【答案】A;
【解析】解:、流星划过夜空,属于点动成线,本选项符合题意.
、打开折扇,属于线动成面,本选项不符合题意.
、汽车雨刷的转动,属于线动成面,本选项不符合题意.
、旋转门的旋转,属于面动成体,本选项不符合题意,
故选:
根据从运动的观点来看点动成线,线动成面,面动成体可得答案.
此题主要考查了点、线、面、体,关键是掌握四者之间的关系.
12.【答案】B;
【解析】解:根据展开图中各种符号的特征和位置,可得墨水在盒子里面.
故选:
在验证立方体的展开图时,要细心观察每一个标志的位置是否一致,然后进行判断.
此题主要考查正方体的表面展开图及空间想象能力.易错易混点:学生对相关图的位置想象不准确,从而错选,解决这类问题时,不妨动手实际操作一下,即可解决问题.
13.【答案】D;
【解析】解:根据各个选项中的几何体的形体特征可知,选项中的几何体不能绕其中一条直线旋转一周得到,
故选:
根据“面动成体”进行判断即可.
此题主要考查“面动成体”,理解点、线、面、体的意义以及相互关系是正确判断的关键.
14.【答案】C;
【解析】解:、不能围成棱柱,底面应该在两侧,故此选项不符合题意;
、不能围成棱柱,侧面有个,底面是三角形,应该是四边形才行,故此选项不符合题意;
、能围成三棱柱,侧面有个,底面是三角形,故此选项符合题意;
、不能围成棱柱,底面应该在两侧,故此选项不符合题意;
故选:
根据棱柱的特点进行分析即可.
此题主要考查了展开图折叠成几何体,关键是通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开.
15.【答案】A;
【解析】解:将图的正方形放在图中的①的位置出现重叠的面,所以不能围成正方体.
故选:
由平面图形的折叠及正方体的表面展开图的特点解题.
此题主要考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.
16.【答案】潭;
【解析】解:由正方体表面展开图的“相间、端是对面”可知,
“建”与“平”是相对的面,
“设”与“明”是相对的面,
“文”与“潭”是相对的面,
故答案为:潭.
根据正方体的表面展开图的特征进行判断即可.
此题主要考查正方体的展开与折叠,掌握正方体的表面展开图的特征是正确判断的前提.
17.【答案】16π或12π;
【解析】解:①以的直角边为轴旋转,可得到,底面半径为,高为的圆锥体,
因此体积为,
②以的直角边为轴旋转,可得到,底面半径为,高为的圆锥体,
因此体积为,
故答案为:或
分两种情况,分别利用圆锥体体积的计算方法进行计算即可.
此题主要考查点、线、面、体,掌握圆锥体体积的计算方法是得出正确答案的前提.
18.【答案】6;
【解析】解:由图一、二可得:标的与标,,,的面相邻,所以与相对;
由图二、三可得标的与标,,,的面相邻,所以与相对;
由图一、三可得标的与标,,的面相邻,所以与相对;
故既与又与相邻的是或,在上在右就是,在上在右就是所以此题答案是
故答案为:
利用正方体及其表面展开图的特点解题.
此题主要考查正方体相对两个面的文字问题,通过三个正方体中能看到的数字推出三组相对的数字是完成本题的关键.
19.【答案】160π;
【解析】解:由题意得,旋转后是底面半径为,高为的圆柱体,
因此体积为,
故答案为:
根据圆柱体体积的计算方法进行计算即可.
此题主要考查点、线、面、体,掌握圆柱体体积的计算方法是得出正确答案的前提.
20.【答案】线 点 一 曲;
【解析】解:面与面相交得到线,线与线相交得到点,圆锥的侧面和底面相交成一条线,这条线是曲的,
故答案为:线;点;一;曲.
根据点、线、面、体的概念以及圆锥的形状特点解答.
此题主要考查圆锥的知识,掌握圆锥的形状特点是解答该题的关键.
21.【答案】解:(1)如图,四种情况.
(2)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为a cm,则长与宽相等为4a cm,
∵长方体纸盒所有棱长的和是720cm,
∴4(a+4a+4a)=720,解得a=20cm,
∴这个长方体纸盒的体积为:20×80×80=128000(立方厘米).;
【解析】
根据长方体的展开图的情况可知有四种情况;
设最短的棱长高为,则长与宽相等为,根据棱长的和是,列出方程可求出长宽高,即可求出长方体纸盒的体积.
此题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
22.【答案】解:①以长为4cm的边所在的直线为轴,旋转一周可得到一个底面半径为5cm,高为4cm的圆柱体,
因此,体积为π×52×4=100π(c),
②以宽为4cm的边所在的直线为轴,旋转一周可得到一个底面半径为4cm,高为5cm的圆柱体,
因此,体积为π×42×5=80π(c),
答:绕它的一条边所在直线旋转一周,得到的圆柱体的体积为100πc或80πc.;
【解析】
以不同的边所在的直线为轴,可以得到两个不同的圆柱体,分两种情况依据圆柱体的体积的计算方法进行解答即可.
此题主要考查点、线、面、体,掌握圆柱体体积的计算方法是正确解答的前提.
23.【答案】解:设圆柱的高是hcm,根据题意得:
π×1.52h=4×3×2,
∴h≈3.4,
答:圆柱的高约是3.4cm.;
【解析】
直接利用圆柱体体积公式计算得出答案.
此题主要考查了认识立体图形,正确掌握圆柱体体积公式是解题关键.
24.【答案】解:如图,绕长旋转得到的圆柱的底面半径为,高为,体积;
如图,绕宽旋转得到的圆柱底面半径为,高为,体积.
因此绕宽旋转得到的圆柱体积大.;
【解析】绕长旋转得到的圆柱的底面半径为,高为,从而计算体积即可;绕宽旋转得到的圆柱底面半径为,高为,从而计算体积进行比较即可.
该题考查了点、线、面、体的知识,熟记常见平面图形旋转可得到什么立体图形是解决本题的关键,另外要掌握圆柱的体积计算公式.
