华东师大版数学七年级上册 1.1 数学伴我们成长课件(共23张PPT)
文档属性
| 名称 | 华东师大版数学七年级上册 1.1 数学伴我们成长课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 258.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
1.3 数学伴我们成长
你会查数吗?
游戏:抢20
规则:
两个人轮流查数,每个人按正整数的顺序,从1开始,查一个数或两个数,谁先查到20谁赢。
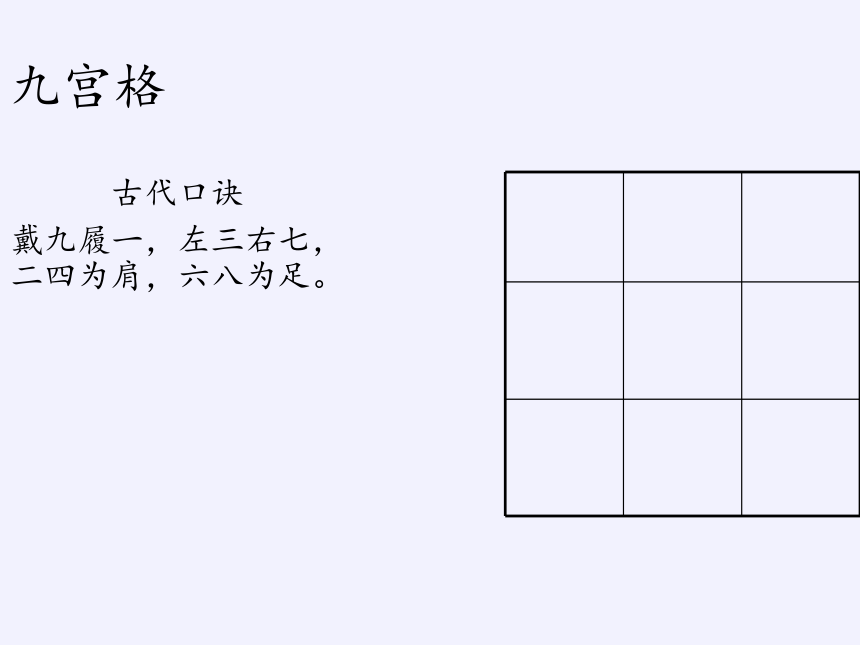
九宫格
将1至9九个正整数填到3×3的正方形格子中,使其横、竖、斜各个方向上的三个数的和都相等。
九宫格
古代口诀
戴九履一,左三右七,二四为肩,六八为足。
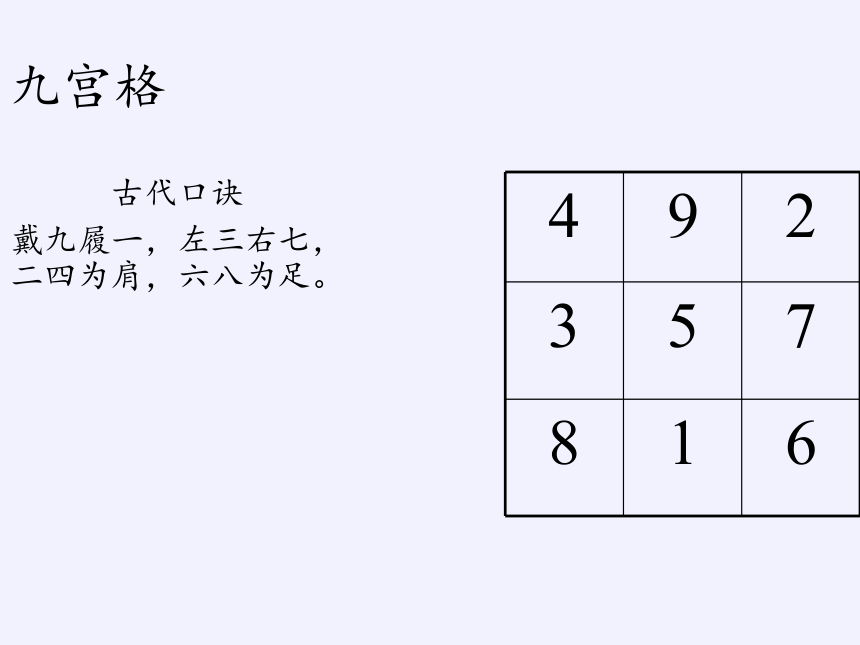
九宫格
古代口诀
戴九履一,左三右七,二四为肩,六八为足。
4 9 2
3 5 7
8 1 6
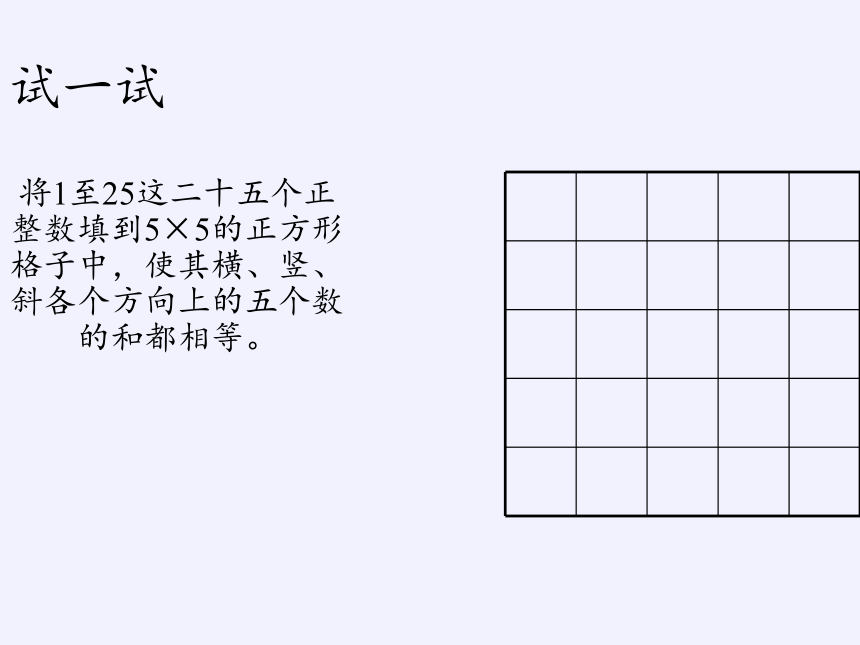
试一试
将1至25这二十五个正整数填到5×5的正方形格子中,使其横、竖、斜各个方向上的五个数的和都相等。
7
8
9
10
13
11
12
14
15
16
17
20
18
19
21
22
23
24
27
25
26
28
29
30
31
1
2
3
6
4
5
日
一
二
三
六
四
五
2016年08月
图形的总面积为10平方厘米
请问阴影部分的面积是多少?为什么?
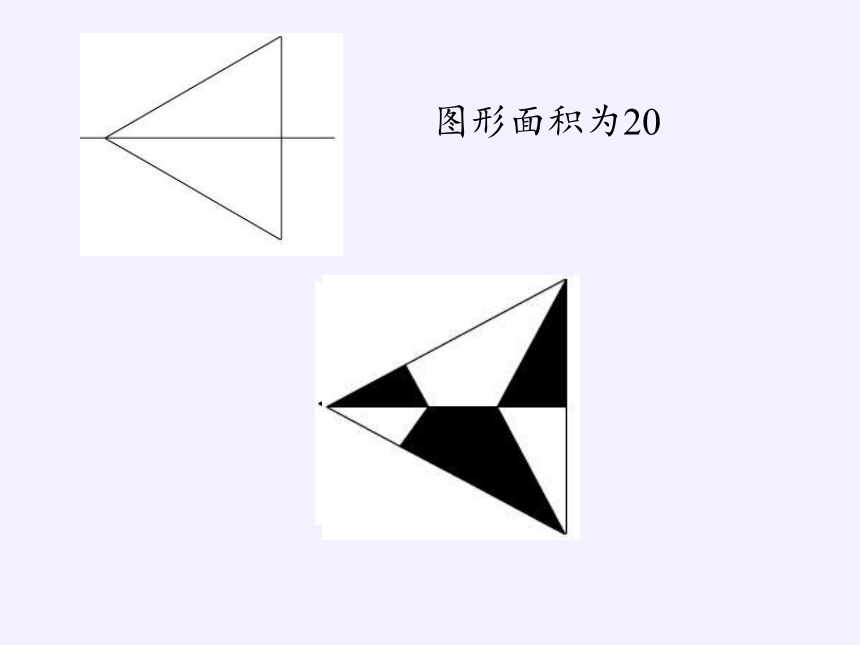
图形面积为20
(1)
(2)
(3)
A
D
C
B
与奇数(单数)条边相连的点叫做奇点;
与偶数(双数)条边相连的点叫做偶点。
图1中的A、C为奇点,B、D为偶点。
奇点
偶点
A
B
C
H
D
G
F
E
1.凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。例如,此图都是偶点,可以一笔画出
A
D
C
B
2、凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点终点。
大数学家欧拉与七桥问题
沿着俄国和波兰的边界,有一条长长的布格河。
布格河有两条支流,它们在城中心会合后,成为一条主流,叫做大河。在两条支流与大河之间,夹着两块小岛。在岛与两岸间有七座桥梁相连。有人提出这样一个问题:能不能一次走遍所有的七座桥,而每座桥只准经过一次?这就是著名的“七桥问题”。
问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决。最后,人们只好把这个问题向俄国科学院院士欧拉提出,请他帮助解决。
A
G
F
E
D
B
C
H
如果你是欧拉,那么,你能用刚刚你学过的知识进行解答吗?
如果在图中可以添加一条线,使得图形能够一笔画出来,你会怎么做呢?
谈一谈 说一说
通过刚刚的几个数学活动
你有怎样的收获和体会?
你认为应该如何面对初中的数学学习?
在数学学科,你有怎样的学习计划?
谢 谢
1.3 数学伴我们成长
你会查数吗?
游戏:抢20
规则:
两个人轮流查数,每个人按正整数的顺序,从1开始,查一个数或两个数,谁先查到20谁赢。
九宫格
将1至9九个正整数填到3×3的正方形格子中,使其横、竖、斜各个方向上的三个数的和都相等。
九宫格
古代口诀
戴九履一,左三右七,二四为肩,六八为足。
九宫格
古代口诀
戴九履一,左三右七,二四为肩,六八为足。
4 9 2
3 5 7
8 1 6
试一试
将1至25这二十五个正整数填到5×5的正方形格子中,使其横、竖、斜各个方向上的五个数的和都相等。
7
8
9
10
13
11
12
14
15
16
17
20
18
19
21
22
23
24
27
25
26
28
29
30
31
1
2
3
6
4
5
日
一
二
三
六
四
五
2016年08月
图形的总面积为10平方厘米
请问阴影部分的面积是多少?为什么?
图形面积为20
(1)
(2)
(3)
A
D
C
B
与奇数(单数)条边相连的点叫做奇点;
与偶数(双数)条边相连的点叫做偶点。
图1中的A、C为奇点,B、D为偶点。
奇点
偶点
A
B
C
H
D
G
F
E
1.凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。例如,此图都是偶点,可以一笔画出
A
D
C
B
2、凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点终点。
大数学家欧拉与七桥问题
沿着俄国和波兰的边界,有一条长长的布格河。
布格河有两条支流,它们在城中心会合后,成为一条主流,叫做大河。在两条支流与大河之间,夹着两块小岛。在岛与两岸间有七座桥梁相连。有人提出这样一个问题:能不能一次走遍所有的七座桥,而每座桥只准经过一次?这就是著名的“七桥问题”。
问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决。最后,人们只好把这个问题向俄国科学院院士欧拉提出,请他帮助解决。
A
G
F
E
D
B
C
H
如果你是欧拉,那么,你能用刚刚你学过的知识进行解答吗?
如果在图中可以添加一条线,使得图形能够一笔画出来,你会怎么做呢?
谈一谈 说一说
通过刚刚的几个数学活动
你有怎样的收获和体会?
你认为应该如何面对初中的数学学习?
在数学学科,你有怎样的学习计划?
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
