湖南省澧县张公庙中学2021-2022学年湘教版八年级上学期期末数学复习试卷(一)(Word版,附答案)
文档属性
| 名称 | 湖南省澧县张公庙中学2021-2022学年湘教版八年级上学期期末数学复习试卷(一)(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 21:57:45 | ||
图片预览

文档简介
湖南省澧县张公庙中学2021-2022学年湘教版八年级数学上册期末复习试卷(一)
一.选择题(共10小题,每小题3分,共30分)
1.的相反数是
A. B.3 C. D.
2.我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为
A. B. C. D.
3.下列命题是真命题的个数为
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2 B.3 C.4 D.5
4.下列各组的分式不一定相等的是
A.与 B.与
C.与 D.与
5.如图,在中,是中线,是角平分线,是高,则下列说法中错误的是
A. B. C. D.
6.不等式组中两个不等式的解集,在数轴上表示正确的是
A. B.
C. D.
7.随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递40件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件件,根据题意可列方程为
A. B.
C. D.
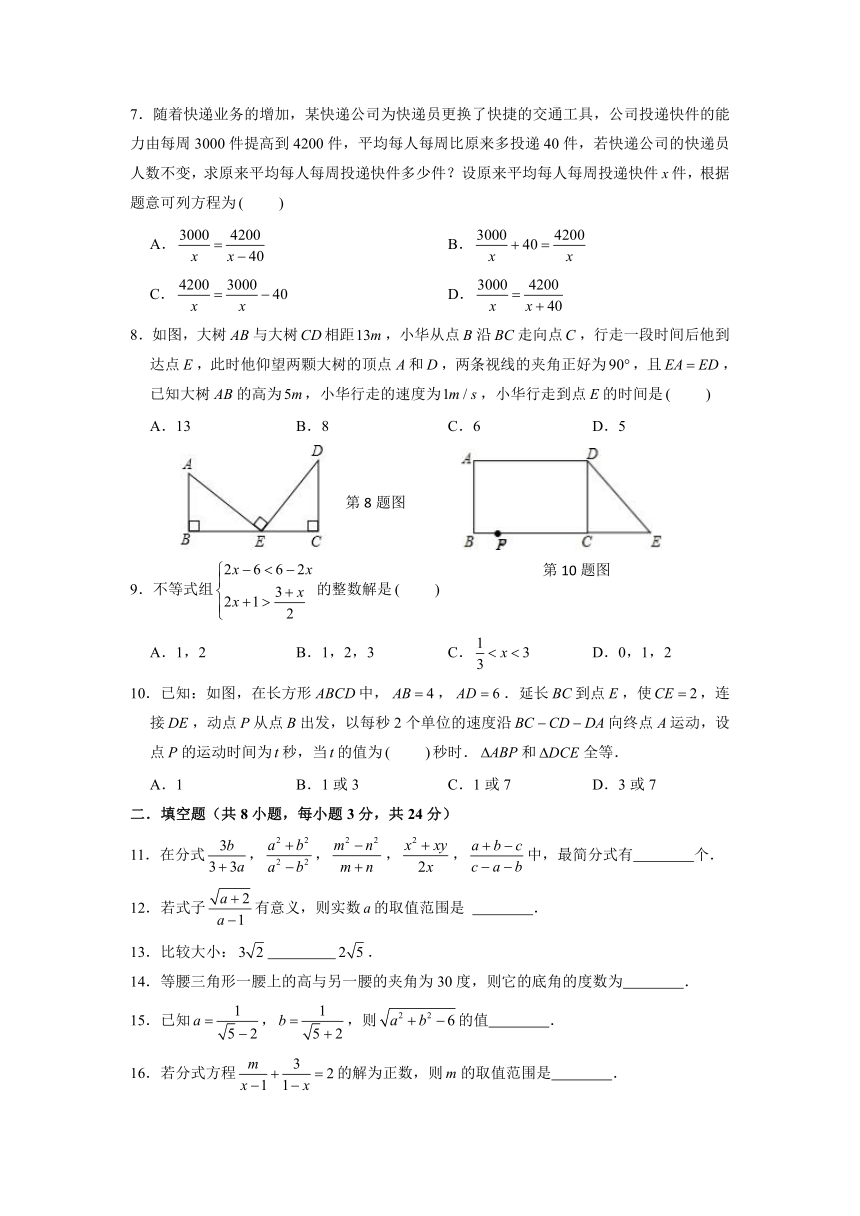
8.如图,大树与大树相距,小华从点沿走向点,行走一段时间后他到达点,此时他仰望两颗大树的顶点和,两条视线的夹角正好为,且,已知大树的高为,小华行走的速度为,小华行走到点的时间是
A.13 B.8 C.6 D.5
9.不等式组的整数解是
A.1,2 B.1,2,3 C. D.0,1,2
10.已知:如图,在长方形中,,.延长到点,使,连接,动点从点出发,以每秒2个单位的速度沿向终点运动,设点的运动时间为秒,当的值为 秒时.和全等.
A.1 B.1或3 C.1或7 D.3或7
二.填空题(共8小题,每小题3分,共24分)
11.在分式,,,,中,最简分式有 个.
12.若式子有意义,则实数的取值范围是 .
13.比较大小: .
14.等腰三角形一腰上的高与另一腰的夹角为30度,则它的底角的度数为 .
15.已知,,则的值 .
16.若分式方程的解为正数,则的取值范围是 .
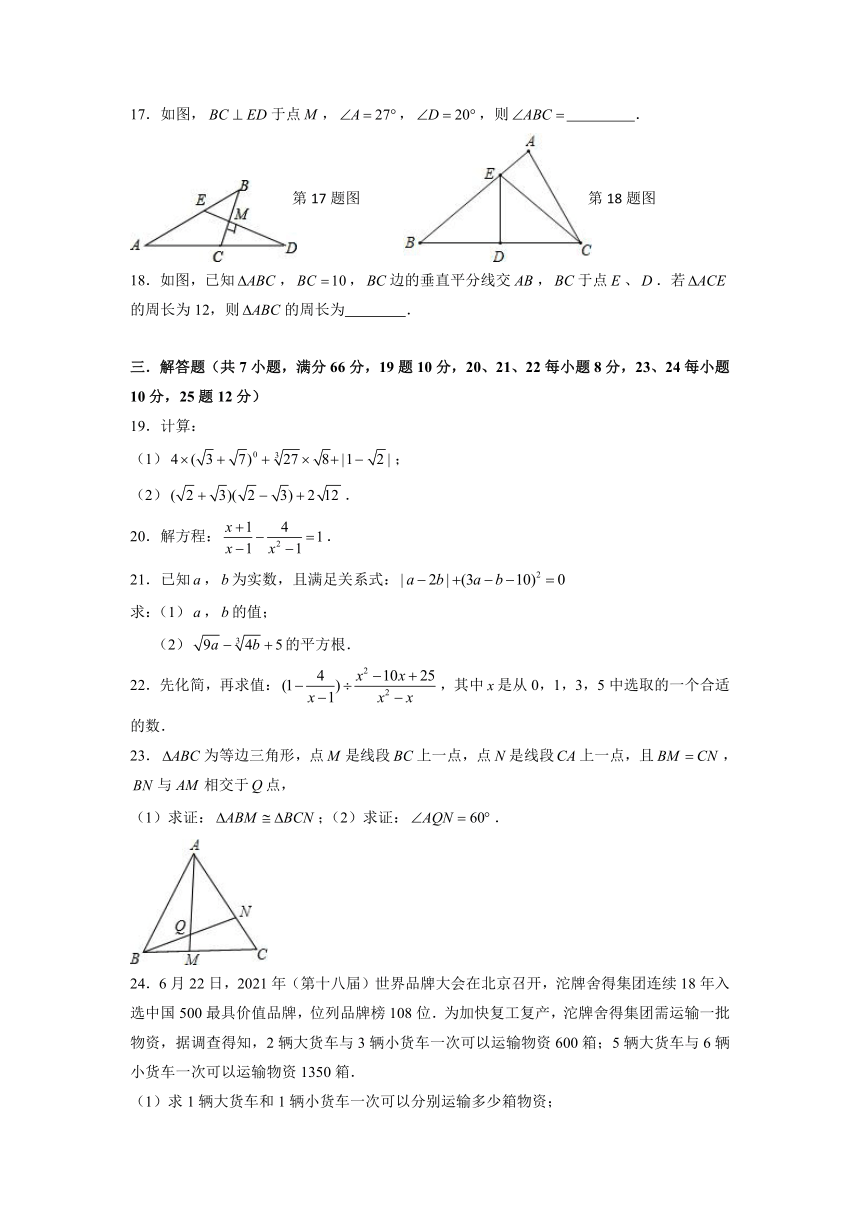
17.如图,于点,,,则 .
18.如图,已知,,边的垂直平分线交,于点、.若的周长为12,则的周长为 .
三.解答题(共7小题,满分66分,19题10分,20、21、22每小题8分,23、24每小题10分,25题12分)
19.计算:
(1);
(2).
20.解方程:.
21.已知,为实数,且满足关系式:
求:(1),的值;
(2)的平方根.
22.先化简,再求值:,其中是从0,1,3,5中选取的一个合适的数.
23.为等边三角形,点是线段上一点,点是线段上一点,且,与相交于点,
(1)求证:;(2)求证:.
24.6月22日,2021年(第十八届)世界品牌大会在北京召开,沱牌舍得集团连续18年入选中国500最具价值品牌,位列品牌榜108位.为加快复工复产,沱牌舍得集团需运输一批物资,据调查得知,2辆大货车与3辆小货车一次可以运输物资600箱;5辆大货车与6辆小货车一次可以运输物资1350箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少.最少费用是多少?
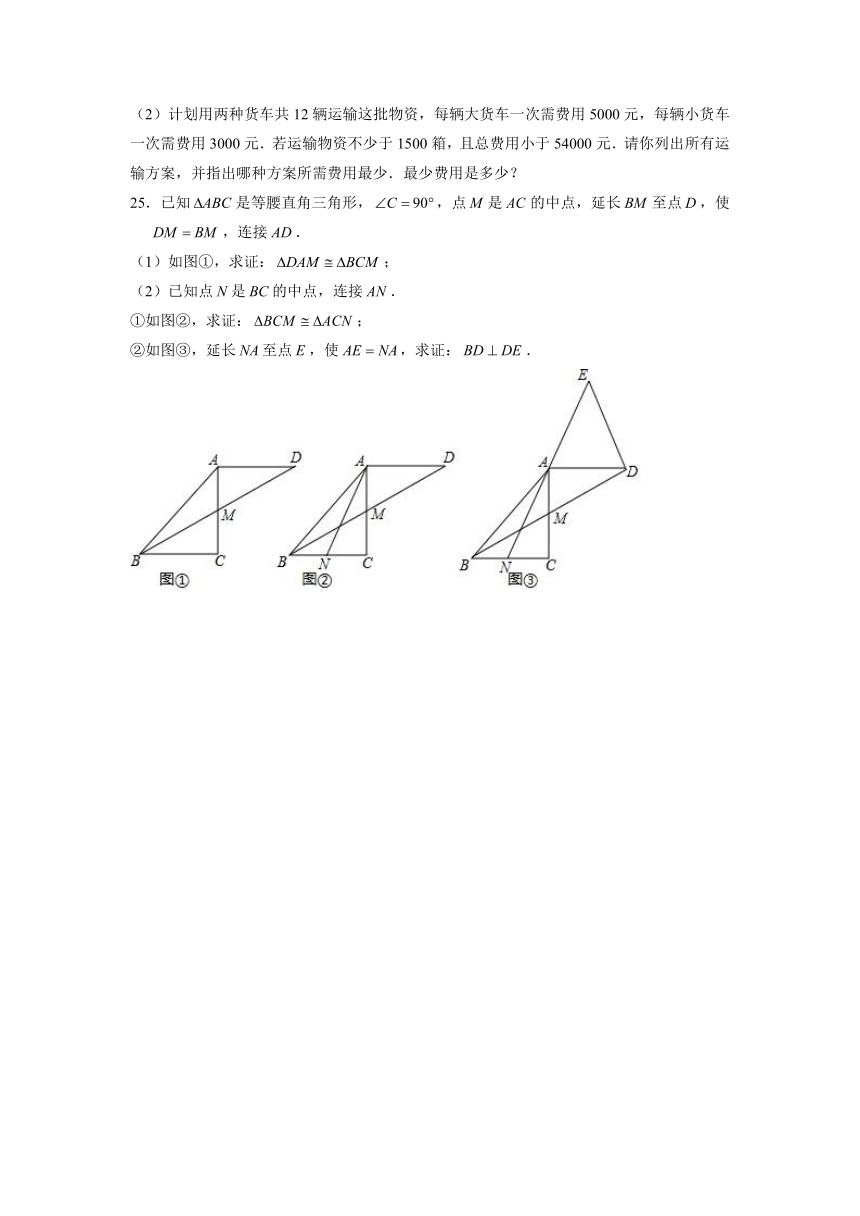
25.已知是等腰直角三角形,,点是的中点,延长至点,使,连接.
(1)如图①,求证:;
(2)已知点是的中点,连接.
①如图②,求证:;
②如图③,延长至点,使,求证:.
湖南省澧县张公庙中学2021-2022学年湘教版八年级数学上册期末复习试卷(一)参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. 1 . 12. 且 . 13. . 14. 或 .
15. . 16. 且 . 17. . 18. 22 .
三.解答题(共7小题)
19.计算:
(1);
(2).
【解】:(1)原式
;
(2)原式
.
20.解方程:.
【解】:方程两边同乘,得
,
整理得,
解得.
检验:当时,,
所以是增根,应舍去.
原方程无解.
21.已知,为实数,且满足关系式:
求:(1),的值;
(2)的平方根.
【解】:(1),为实数,且满足关系式:
,解得;
(2),,
原式
.
,
的平方根是.
22.先化简,再求值:,其中是从0,1,3,5中选取的一个合适的数.
【解】:原式
,
当时,原式.
23.为等边三角形,点是线段上一点,点是线段上一点,且,与相交于点,
(1)求证:;
(2)求证:.
【证明】:(1)为等边三角形,
,
在和中
,
;
(2)(已证).
,
.
24.6月22日,2021年(第十八届)世界品牌大会在北京召开,沱牌舍得集团连续18年入选中国500最具价值品牌,位列品牌榜108位.为加快复工复产,沱牌舍得集团需运输一批物资,据调查得知,2辆大货车与3辆小货车一次可以运输物资600箱;5辆大货车与6辆小货车一次可以运输物资1350箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少.最少费用是多少?
【解】:(1)设1辆大货车一次运输箱物资,1辆小货车一次运输箱物资,
由题意可得:, 解得:,
答:1辆大货车一次运输150箱物资,1辆小货车一次运输100箱物资;
(2)设有辆大货车,则有辆小货车,
由题意可得:,
解得,
为正整数,
,7,8,
共有三种运输方案,
方案一:大货车6辆,小货车6辆,
方案二:大货车7辆,小货车5辆.
方案三:大货车8辆,小货车4辆,
每辆大货车一次需费用5000元,每辆小货车一次需费用3000元,计划用两种货车共12辆运输这批物资,
大货车辆数越少,费用越低,
方案一所需费用最少,此时费用为(元,
答:方案一:大货车6辆,小货车6辆,方案二:大货车7辆,小货车5辆.方案三:大货车8辆,小货车4辆,其中方案一所需费用最少,最少费用为48000元.
25.已知是等腰直角三角形,,点是的中点,延长至点,使,连接.
(1)如图①,求证:;
(2)已知点是的中点,连接.
①如图②,求证:;
②如图③,延长至点,使,求证:.
【证明】:(1)点是中点,
,
在和中,
,
;
(2)①点是中点,点是中点,
,,
是等腰直角三角形,
,
,
在和中,
,
;
②证明:取中点,连接,
则,
,
,,
,
,,
,
,,
在和中,
,
,
,,
,
为中点,
,
在和中,
,
,
,
,
.
第10题图
第8题图
第18题图
第17题图
一.选择题(共10小题,每小题3分,共30分)
1.的相反数是
A. B.3 C. D.
2.我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为
A. B. C. D.
3.下列命题是真命题的个数为
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2 B.3 C.4 D.5
4.下列各组的分式不一定相等的是
A.与 B.与
C.与 D.与
5.如图,在中,是中线,是角平分线,是高,则下列说法中错误的是
A. B. C. D.
6.不等式组中两个不等式的解集,在数轴上表示正确的是
A. B.
C. D.
7.随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递40件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件件,根据题意可列方程为
A. B.
C. D.
8.如图,大树与大树相距,小华从点沿走向点,行走一段时间后他到达点,此时他仰望两颗大树的顶点和,两条视线的夹角正好为,且,已知大树的高为,小华行走的速度为,小华行走到点的时间是
A.13 B.8 C.6 D.5
9.不等式组的整数解是
A.1,2 B.1,2,3 C. D.0,1,2
10.已知:如图,在长方形中,,.延长到点,使,连接,动点从点出发,以每秒2个单位的速度沿向终点运动,设点的运动时间为秒,当的值为 秒时.和全等.
A.1 B.1或3 C.1或7 D.3或7
二.填空题(共8小题,每小题3分,共24分)
11.在分式,,,,中,最简分式有 个.
12.若式子有意义,则实数的取值范围是 .
13.比较大小: .
14.等腰三角形一腰上的高与另一腰的夹角为30度,则它的底角的度数为 .
15.已知,,则的值 .
16.若分式方程的解为正数,则的取值范围是 .
17.如图,于点,,,则 .
18.如图,已知,,边的垂直平分线交,于点、.若的周长为12,则的周长为 .
三.解答题(共7小题,满分66分,19题10分,20、21、22每小题8分,23、24每小题10分,25题12分)
19.计算:
(1);
(2).
20.解方程:.
21.已知,为实数,且满足关系式:
求:(1),的值;
(2)的平方根.
22.先化简,再求值:,其中是从0,1,3,5中选取的一个合适的数.
23.为等边三角形,点是线段上一点,点是线段上一点,且,与相交于点,
(1)求证:;(2)求证:.
24.6月22日,2021年(第十八届)世界品牌大会在北京召开,沱牌舍得集团连续18年入选中国500最具价值品牌,位列品牌榜108位.为加快复工复产,沱牌舍得集团需运输一批物资,据调查得知,2辆大货车与3辆小货车一次可以运输物资600箱;5辆大货车与6辆小货车一次可以运输物资1350箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少.最少费用是多少?
25.已知是等腰直角三角形,,点是的中点,延长至点,使,连接.
(1)如图①,求证:;
(2)已知点是的中点,连接.
①如图②,求证:;
②如图③,延长至点,使,求证:.
湖南省澧县张公庙中学2021-2022学年湘教版八年级数学上册期末复习试卷(一)参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. 1 . 12. 且 . 13. . 14. 或 .
15. . 16. 且 . 17. . 18. 22 .
三.解答题(共7小题)
19.计算:
(1);
(2).
【解】:(1)原式
;
(2)原式
.
20.解方程:.
【解】:方程两边同乘,得
,
整理得,
解得.
检验:当时,,
所以是增根,应舍去.
原方程无解.
21.已知,为实数,且满足关系式:
求:(1),的值;
(2)的平方根.
【解】:(1),为实数,且满足关系式:
,解得;
(2),,
原式
.
,
的平方根是.
22.先化简,再求值:,其中是从0,1,3,5中选取的一个合适的数.
【解】:原式
,
当时,原式.
23.为等边三角形,点是线段上一点,点是线段上一点,且,与相交于点,
(1)求证:;
(2)求证:.
【证明】:(1)为等边三角形,
,
在和中
,
;
(2)(已证).
,
.
24.6月22日,2021年(第十八届)世界品牌大会在北京召开,沱牌舍得集团连续18年入选中国500最具价值品牌,位列品牌榜108位.为加快复工复产,沱牌舍得集团需运输一批物资,据调查得知,2辆大货车与3辆小货车一次可以运输物资600箱;5辆大货车与6辆小货车一次可以运输物资1350箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少.最少费用是多少?
【解】:(1)设1辆大货车一次运输箱物资,1辆小货车一次运输箱物资,
由题意可得:, 解得:,
答:1辆大货车一次运输150箱物资,1辆小货车一次运输100箱物资;
(2)设有辆大货车,则有辆小货车,
由题意可得:,
解得,
为正整数,
,7,8,
共有三种运输方案,
方案一:大货车6辆,小货车6辆,
方案二:大货车7辆,小货车5辆.
方案三:大货车8辆,小货车4辆,
每辆大货车一次需费用5000元,每辆小货车一次需费用3000元,计划用两种货车共12辆运输这批物资,
大货车辆数越少,费用越低,
方案一所需费用最少,此时费用为(元,
答:方案一:大货车6辆,小货车6辆,方案二:大货车7辆,小货车5辆.方案三:大货车8辆,小货车4辆,其中方案一所需费用最少,最少费用为48000元.
25.已知是等腰直角三角形,,点是的中点,延长至点,使,连接.
(1)如图①,求证:;
(2)已知点是的中点,连接.
①如图②,求证:;
②如图③,延长至点,使,求证:.
【证明】:(1)点是中点,
,
在和中,
,
;
(2)①点是中点,点是中点,
,,
是等腰直角三角形,
,
,
在和中,
,
;
②证明:取中点,连接,
则,
,
,,
,
,,
,
,,
在和中,
,
,
,,
,
为中点,
,
在和中,
,
,
,
,
.
第10题图
第8题图
第18题图
第17题图
同课章节目录
