中位线定理

(共18张PPT)
九年级数学(上)第一章：特殊四边形
学 习 目 标
知识目标 :知道三角形的中位线概念,能说出三角形的中位线定理.
能力目标:经历探索、猜想、证明的过程，进一步发展推理论证的能力.
情感目标:通过自主探究、猜想、验证，获得亲自参与研究的情感体验，增强学习热情.
A
B
C
D
E
美丽校园
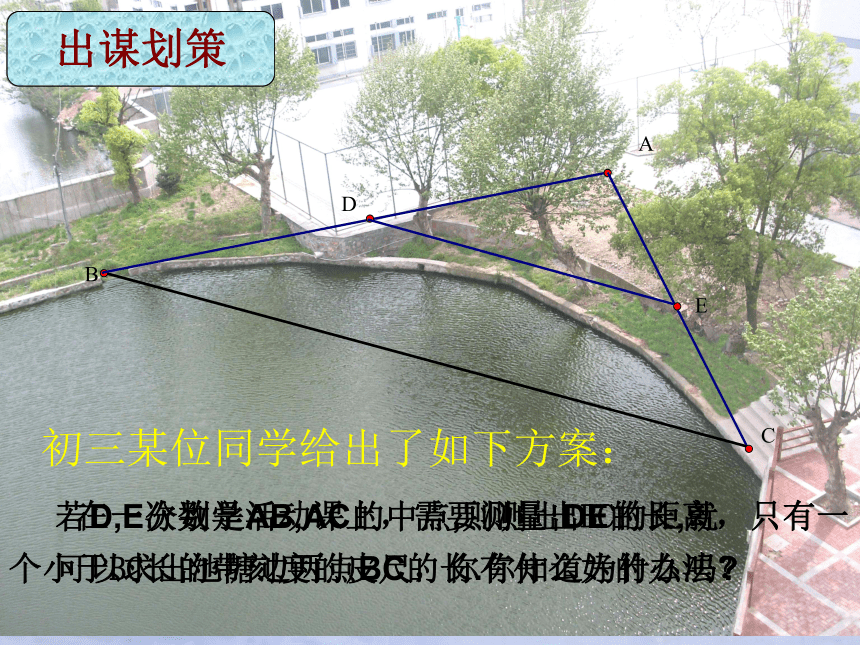
在一次数学活动课上，需要测量出BC的距离，只有一个小于BC长的带刻度的皮尺，你有什么好的办法？
初三某位同学给出了如下方案：
若D,E分别是AB,AC的中点,则测出DE的长,就可以求出池塘边两点BC的长.你知道为什么吗
出谋划策
温馨提示
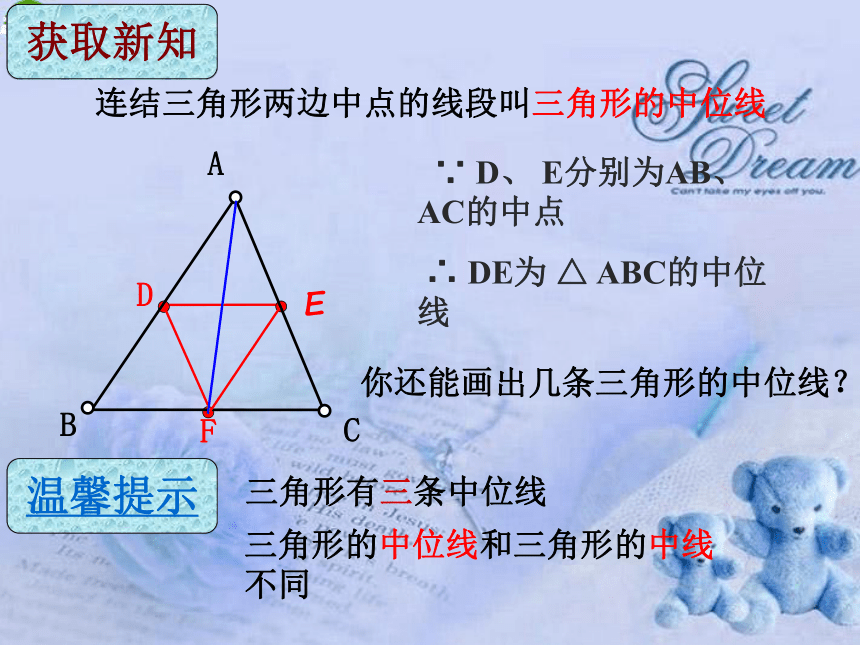
连结三角形两边中点的线段叫三角形的中位线
三角形有三条中位线
∵ D、 E分别为AB、 AC的中点
∴ DE为 △ ABC的中位线
三角形的中位线和三角形的中线不同
E
D
F
A
C
B
获取新知
你还能画出几条三角形的中位线？
B
F
D
A
C
E
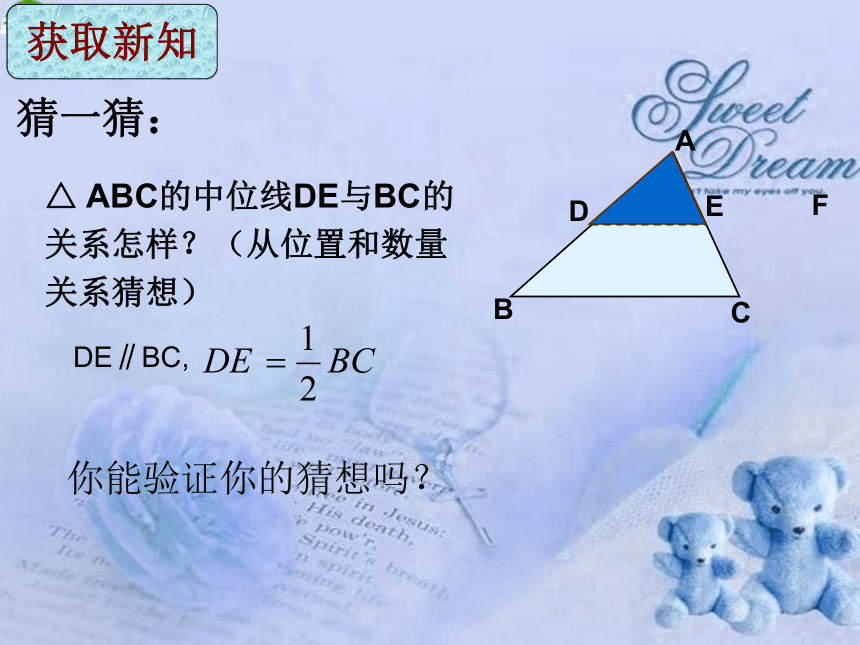
猜一猜：
△ ABC的中位线DE与BC的关系怎样？（从位置和数量关系猜想）
获取新知
DE∥BC,
你能验证你的猜想吗？
已知：如图，DE是△ABC的 中位线
求证：DE∥BC，DE＝ BC
1
2
B C
A
D
E
证明：延长DE至F，使EF＝DE，连接CF
∵AE＝CE，∠AED＝∠CEF，
∴△ADE≌△CFE
∴AD＝CF，∠ADE＝∠F
∴BD∥CF
∵AD＝BD
∴BD＝CF
∴四边形BCFD是平行四边形( )
∴DF∥BC，DF＝BC( )
∴DE∥BC，DE＝
BC
1
2
F
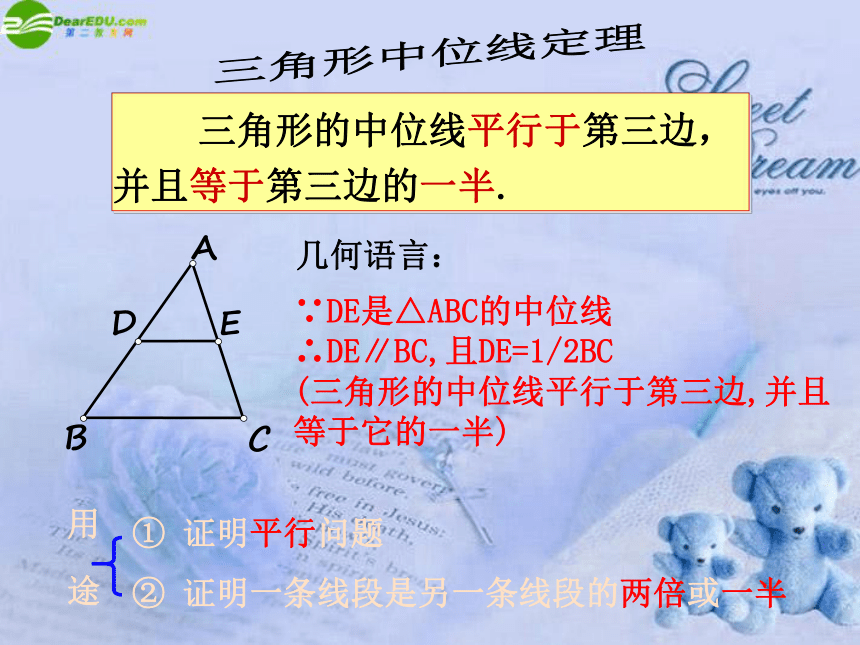
　　三角形的中位线平行于第三边，并且等于第三边的一半.
几何语言：
∵DE是△ABC的中位线
∴DE∥BC,且DE=1/2BC
(三角形的中位线平行于第三边,并且等于它的一半)
C
E
D
B
A
① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半
用 途
A
C
B
E
D
F
初试身手
练习1.如图，在△ABC中，D、E分别是AB、AC的中点
若∠ADE=65°，则∠B= 度，为什么？
若BC=8cm，则DE= cm，为什么？
65
4
若AC=4cm,BC=6cm，AB=8cm，
则△DEF的周长=______
练习1.如图，在△ABC中，D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24，△DEF的周长是_____
12
1、 三角形三条中位线围成的三角形的周长与原三角形的周长的关系？
探究活动二
2、三角形三条中位线围成的三角形的面积与原三角形的面积的关系？
图中有_____个平行四边形
若△ABC的面积为24，△DEF的面积是_____
3
6
通过刚才的学习，我们探索并发现连接任意三角形三边中点所得的三角形的部分规律，对于任意四边形，连接四边中点所得到的四边形又有何规律呢？请你动手画一画！
A
B
C
D
E
F
G
H
C
E
D
B
A
探究活动三
已知：如图，在四边形ABCD中，E、F、G、H分别是 AB、BC、CD、DA的中点.
求证：四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
证明：如图，连接AC
∴ EF是△ABC的中位线
同理得：
∴四边形EFGH是平行四边形( )
①有中点连线而无三角形,要作辅助线产生三角形
探究活动三
∵ E、F、是AB、BC、的中点
1.已知: 如图,DE,EF是△ABC的两条中位线.求证:四边形BFED是平行四边形.
2.如图,DE是△ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.
D
B
C
F
E
A
(第1题)
F
E
D
C
B
A
O
(第2题)
比一比
有三角形而无中位线,要连结两边中点得中位线
已知，
如图， A1 、 B1 、 C1 分别是△ABC 三边中点， A2 、 B2 、 C2分别是△ A1B1C1 三边中点， A3 、 B3 、 C3分别是△ A2B2C2 三边中点，依次……得△AnBnCn，
△ ABC的周长是24面积是24
求△ A1B1C1的周长C1和面积S1
挑战自我
求△ A2B2C2的周长C2和面积S2
C1 = S1 =
C2 = S2 =
1、什么叫三角形的中位线？
连接三角形两边中点的线段叫做三角形的中位线。
2、中位线的性质定理？
三角形的中位线平行于第三边，并且等于第三边的一半。
3 、辅助线