2021北师大版九上第四章图形的相似选择与填空培优试题(二)(Word版,附答案解析)
文档属性
| 名称 | 2021北师大版九上第四章图形的相似选择与填空培优试题(二)(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 21:40:56 | ||
图片预览



文档简介
图形的相似选择与填空培优试题(二)
一、单选题
1.(2021八下·相城期末)在四边形 中 ,对角线 与 交于 ,过点 作 的平行线,交 、 于 、 .若 , 与 的面积比为 ,则 的长是( )
A. B. C. D.
2.(2021八下·龙口期末)已知点A(0,3),B(-4,3),以原点O为位似中心,把线段AB缩短为原来的 ,其中点C与点A对应,点D与点B对应.则点D的坐标为( )
A. (-1, ) B. (1,- )
C. ( ,-1)或(- ,1) D. (-1, )或(1,- )
3.(2021·玉林模拟)如图,在菱形 中, ,点E,F分别在 , 上,沿 折叠菱形,使点A落在 边上的点G处,且 于点M,若 (取 , ),则 等于( )
A. B. C. D.
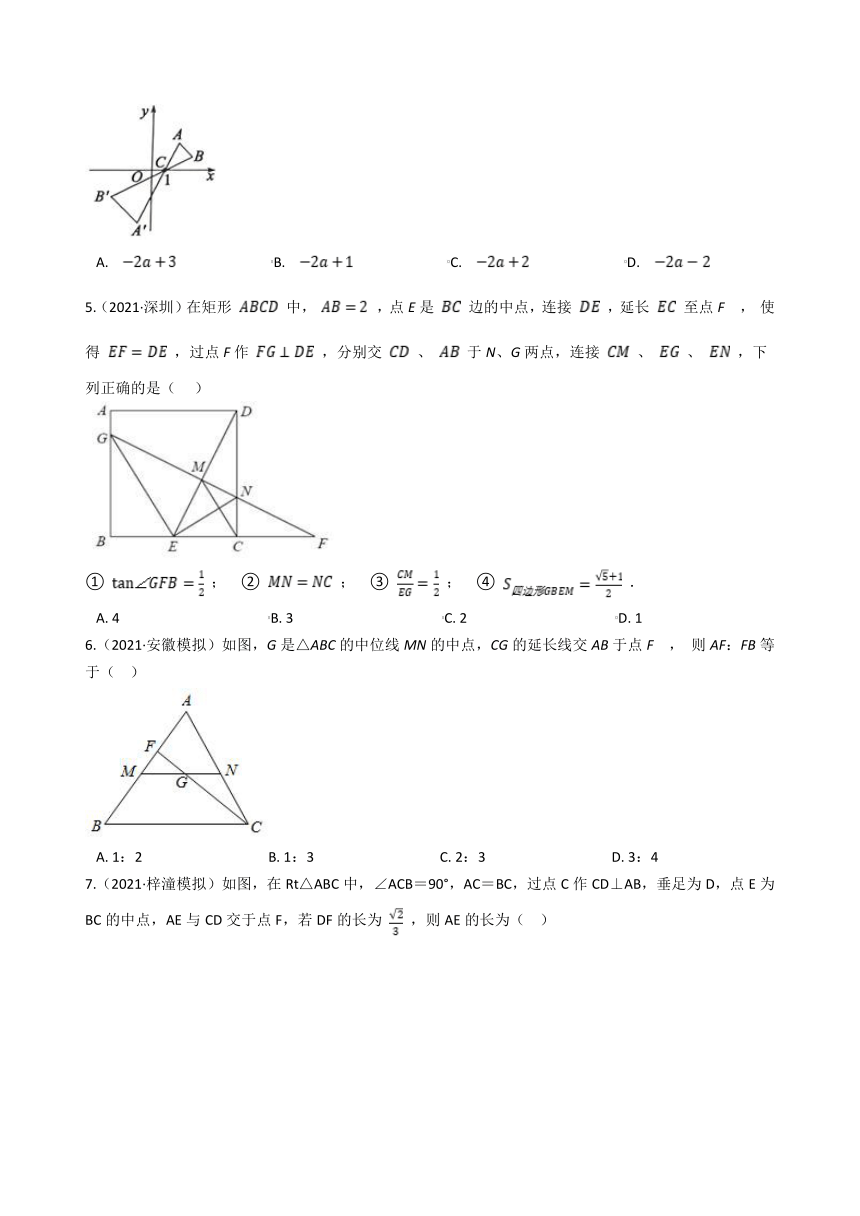
4.(2021·东营)如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( )
A. B. C. D.
5.(2021·深圳)在矩形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得 ,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,下列正确的是( )
① ; ② ; ③ ; ④ .
A. 4 B. 3 C. 2 D. 1
6.(2021·安徽模拟)如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( )
A. 1:2 B. 1:3 C. 2:3 D. 3:4
7.(2021·梓潼模拟)如图,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作CD⊥AB,垂足为D,点E为BC的中点,AE与CD交于点F,若DF的长为 ,则AE的长为( )
A. B. 2 C. D. 2
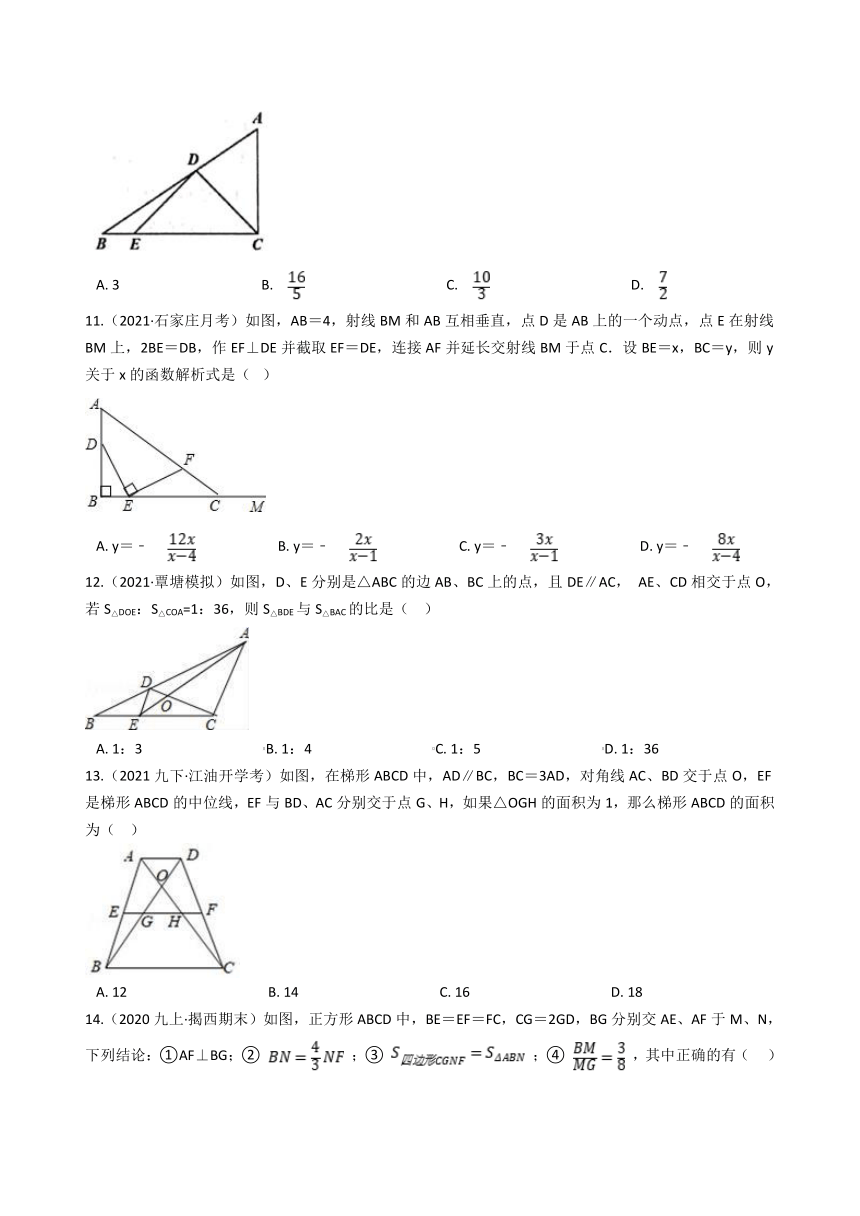
8.(2021·合肥模拟)如图, 中, , ,点 在 的延长线上,且 连接 并延长,过 作 于点 ,若 ,则 的面积为( )
A. 1 B. 2 C. D.
9.(2021·周村模拟)如图,在等边三角形 中, ,点D是边 上一点,且 ,点P是边 上一动点(D,P两点均不与端点重合),作 , 交边 于点E.若 ,当满足条件的点P有且只有一个时,则a的值为( )
A. 4 B. 5 C. D.
10.(2021·杭州)如图,在 中, ,CD是 的角平分线,过点D作 交BC于点E. 和 的面积分别为 和 ,若 ,则 的值为( ).
A. 3 B. C. D.
11.(2021·石家庄月考)如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( )
A. y=﹣ B. y=﹣ C. y=﹣ D. y=﹣
12.(2021·覃塘模拟)如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC, AE、CD相交于点O,若S△DOE:S△COA=1:36,则S△BDE与S△BAC的比是( )
A. 1:3 B. 1:4 C. 1:5 D. 1:36
13.(2021九下·江油开学考)如图,在梯形ABCD中,AD∥BC,BC=3AD,对角线AC、BD交于点O,EF是梯形ABCD的中位线,EF与BD、AC分别交于点G、H,如果△OGH的面积为1,那么梯形ABCD的面积为( )
A. 12 B. 14 C. 16 D. 18
14.(2020九上·揭西期末)如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE、AF于M、N,下列结论:①AF⊥BG;② ;③ ;④ ,其中正确的有( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
15.(2020九上·深圳期末)如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一直线上,顶点B,C,G在同一条直线上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH。以下四个结论:①GH⊥BE;②△EHM∽△FHG;③ ; ,其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
16.(2020九上·福田期中)如图,正方形 的边长为6,点E是 边的中点,连接 与对角线 交于点G,连接 并延长,交 于点F,连接 交 于点H,连接 .以下结论:① ;② ;③ ;④ .其中正确的结论是( )
A. 1 B. 2 C. 3 D. 4
17.(2020九上·邗江月考)如图,已知点A是第一象限内横坐标为2 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长为( ).
A. B. C. 4 D.
18.(2020九上·江苏期中)如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转使∠DPG=∠DAC,且过D作DG⊥PG,连接CG,则CG最小值为( )
A. B. C. D.
19.(2020九上·犍为期中)如图, ∽ , , , ,F是 的中点,若点E是直线 上的动点,连接 ,则 的最小值是( )
A. B. C. D.
20.(2020·昆明模拟)如图,正方形ABCD中, ,点E是对角线AC上一点,连接BE,过点E作 ,交AB于点F,连接DF,交AC于点G,将 沿EF翻折,得到 ,连接DM,交EF于点N,若点F是AB的中点,则 的周长是( )
A. B. C. D.
二、填空题
21.(2021九下·金牛月考)如图,在Rt△ABC中,∠ACB=90°,BC=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP , BP , AP+ =BP的最小值为 .
22.(2021九上·锦州期末)如图,在矩形 中,对角线 , 交于点 ,过点 作 ,交 的延长线于点 ,若 , ,则 的长为________.
23.(2021九上·建湖期末)如图,矩形 中, , , 为 边上的动点,当 时, 与 相似.
24.(2021九上·汝阳期末)如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=________.
25.(2020九上·吉水期末)如图示意图,A点的坐标为(2,2),点C在线段OA上运动(点C不与O、A重合),过点C作CD⊥x轴于D,再以CD为一边在CD右侧画正方形CDEF.连接AF并延长交x轴于B,连接OF.若△BEF与△OEF相似,则点B的坐标是 .
26.(2020九上·龙岗期中)如图,在△ABC中, ,动点P在射线EF上,BP交CE于点D , ∠CBP的平分线交CE于点Q , 当CQ= CE时,EP+BP=20,则BC的长为________.
27.(2020九上·东阿期中)如图,将三角形纸片的一角折叠,使点B落的AC边上的F处,折痕为DE , 已知AB=AC=8,BC=10,若以点E , F , C为顶点的三角形与△ABC相似,那么BE的长是________.
28.(2020九上·青山期中)如图,△ABC、△DCE、△GEF都是正三角形,且B、C、E、F在同一直线上,A、D、G也在同一直线上,设△ABC、△DCE、△GEF的面积分别为S1、S2、S3 . 当S1=4,S2=6时,S3=________.
29.(2020九上·株洲期中)如图, ,点 在 上, 与 交于点 , , ,则 的长为________.
30.(2020九上·织金月考)如图,矩形 的边长 , , 为 的中点, 在边 上,且 , 分别与 、 相交于点 , ,则 的长为 .
31.(2020九上·惠山月考)如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为________.
32.(2020·大通模拟)如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为________.
33.(2020·上城模拟)如图所示,设G是△ABC的重心,过G的直线分别交AB,AC于点P,Q两点,则 =________.
34.(2019·天府新模拟)如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=________.
35.(2021九上·禅城月考)如图,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.若AD、BC所在直线互相垂直, 的值为 .
36.(2021九上·成都开学考)如图,在矩形 中, , ,点 是边 的中点,连接 ,将 沿 折叠得到 , 与 交于点 ,则 的长为 .
37.(2021·牡丹江)如图,矩形ABCD中,AD AB , 点E在BC边上,且AE=AD , DF⊥AE于点F , 连接DE , BF , BF的延长线交DE于点O , 交CD于点G . 以下结论:①AF=DC , ②OF:BF=CE:CG , ③S△BCG S△DFG , ④图形中相似三角形有6对,则正确结论的序号是 .
38.(2021·曾都模拟)如图,在 中, , , , 是 上方一动点,且 , 交 于点E.当点P运动到 时, 的值为 ;随着点P的运动, 的最大值为 .
39.(2021·洪洞模拟)如图,在矩形 中, , 为边 上两点,将矩形 沿 折叠,点 恰好落在 上的 处,且 ,再将矩形 沿过点 的直线折叠,使点 落在 上的 处,折痕交 于点 ,将矩形 再沿 折叠, 与 恰好重合,已知 ,则 .
40.(2021·南沙模拟)如图,在矩形ABCD中,AB=4,AD=5,E是CD边上一点,连结AE , 将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G , 连结DG . 点M、N分别是线段AG , DG上的动点(与端点不重合),且∠DMN=∠DAM , 以下结论:①CE=2;②DM2=DN AF;③DN最小值为1;④若△DMN为等腰三角形,则点M的位置有三种不同情况.其中正确的是 .
41.(2021·周村模拟)如图,在矩形 中, ,E为 上一点,将 沿 折叠,使点C正好落在 边上的F处,作 的平分线交 于N,交 的延长线于M,若 ,则 的长为 .
42.(2021·陕西模拟)已知矩形 , 是 边上一点且 是 边的中点,连接 相交于 两点,则 的面积是 .
43.(2020九上·上海月考)如图, 为 的 边上的点、且 ,中线 被 截得的三线段为 ,则 ________
44.(2020九上·永春期中)如图,已知Rt ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1 , 连结BE1交CD1于D2;过D2作D2E2⊥AC于E2 , 连结BE2交CD1于D3;过D3作D3E3⊥AC于E3 , …,如此继续,可以依次得到点D4 , D5 , …,Dn , 分别记 BD1E1 , BD2E2 , BD3E3 , …, BDnEn的面积为S1 , S2 , S3 , …Sn . 则(1) =________,(2)Sn=________.
45.(2020·西安模拟)如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值________.
46.(2020·青羊模拟)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2 ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为________.
47.(2020·高新模拟)如图,在等腰Rt△ABC中,AC=BC=6 ,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若 = ,则AH的长为________.
48.(2020·哈尔滨模拟)如图所示.△ABC为等腰直角三角形,∠ACB=90°,点M为AB边的中点,点N为射线AC上一点,连接BN,过点C作CD⊥BN于点D。连接MD,作∠BNE=∠BNA,边EN交射线MD于点E,若AB=20 ,MD=14 ,则NE的长为________。
49.(2020九上·丽水期末)如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
( 1 )AE的长为________(用含x的代数式表示);
( 2 )设EK=2KF,则 的值为________.
50.(2020九上·锦江期末)如图,在 中, ,对角线 ,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得 ,连接CF,则 周长的最小值为________.
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】解:∵DC∥AB,
∴△PDC∽△PAB,
∵ ,
∴ ,又AB=2,
∴CD=1,
∵MN∥AB,
∴MN∥CD,
∴△AMP∽△ADC,△BPN∽△BDC,
∴ , ,
∴ , ,
∴MP= ,NP= ,
∴MN=MP+NP= ,
故答案为:C.
【分析】根据平行得到△PDC∽△PAB,可得 ,以及CD=1,再证明△AMP∽△ADC,△BPN∽△BDC,得到 , ,可得MP和NP,从而得到MN.
2.【答案】 D
【解析】【解答】解: 点 , ,以原点 为位似中心,把线段 缩短为原来的 ,得到线段 ,点 与点 对应,
点 的横坐标为: 或 .
点 的纵坐标为: 或 .
所以点D的坐标为(-1, )或(1,- )
故答案为:D.
【分析】根据点的坐标和位似的性质进行求解即可。
3.【答案】 D
【解析】【解答】解:如图,连接AC,交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AO,
∵∠A=60°,
∴∠BAO=30°,
∴AO=AB cos30°= ,
∴AC= ,
∵沿EF折叠菱形,使点A落在BC边上的点G处,
∴EG=AE,
∵EG⊥BD,AC⊥BD,
∴EG∥AC,
∴ ,
又∵EG=AE,
∴ ,
解得AE= ,
∴AE的长为 .
故答案为:D.
【分析】连接AC,交BD于点O,由菱形的性质可得AC⊥BD,AC=2AO,求出∠BAO的度数,表示出AO、AC,由折叠的性质可得:EG=AE,然后根据平行线分线段成比例的性质以及EG=AE可表示出AE.
4.【答案】 A
【解析】【解答】解:设点 的横坐标为 ,
则 、 间的横坐标的差为 , 、 间的横坐标的差为 ,
放大到原来的 倍得到 ,
,
解得: .
故答案为:A.
【分析】设点 的横坐标为 ,根据数轴表示出BC、B'C的横坐标的距离,再根据位似比利时计算即可。
5.【答案】 B
【解析】【解答】
故答案为:① ,①正确;
②∵ , ,
∴ ,
∵ , , ,
∴ ( ),∴ ,∴ ,
∵ , , ,
∴ ( ),∴ ,故②正确;
③∵ , ,∴ ,
∵在 和 中: , ,
∴ ( ),∴ ,
∵ ,∴ ,
又∵ ,
∴ ,∴ ,∴ ,
∵ , ,
∴ ,故③错误;
④由上述可知: , ,∴ ,
∵ ,∴ ,
∴ ,故④正确.
故选B.
【分析】①先证出∠GFB=∠EDC,得出 , 即可判断①正确;
②先证出△DEC≌△FEM,得出EM=EC,从而得出DM=FC,进而证出△DMN≌△FCN,得出MN=NC,即可判断②正确;
③先证出MC∥GE,得出 , 再求出EF,CF的长,得出 , 即可判断③错误;
④先求出BF的长,根据 , 求出GB的长,利用 , 即可判断④正确.
6.【答案】 A
【解析】【解答】 MN是△ABC的中位线
, ,
G是MN的中点
即
又
即:AF:FB .
故答案为:A.
【分析】根据三角形的中位线的性质得到 , 再利用相似三角形的性质和三角形的中位线求出 , 最后整体代入计算即可。
7.【答案】 C
【解析】【解答】解:连接DE,如图所示:
在Rt△ABC中,∠ACB=90°,AC=BC,
∵CD⊥AB,
∴AD=BD,即点D为AB的中点.
∵E为BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,DE= AC,
∴△DEF∽△CAF,
∴DF:CF=DE:AC=1:2,
∴DF= CD= ,
∴CD= .
∴AB=2 .
∵AC=BC,
∴AC2+BC2=2AC2=AB2=8.
∴AC=BC=2.
∴CE=1.
在直角△ACE中,由勾股定理知:
AE= .
故答案为:C.
【分析】连接DE,首先推知ED为△ABC的中位线,然后由中位线的性质得到△DEF∽△CAF,从而求得CD的长度;继而推知AC=BC=2;最后由勾股定理求得AE的长度.
8.【答案】 C
【解析】【解答】解:取AB的中点F,连接CF,
∵∠ACB=90°,∠CBA=30°,
∴∠CAB=60°,FC=FA= AB,
∴△AFC是等边三角形,
∴∠FAC=∠FCA=60°,AC=FC=FA,
∵BA=2AD,
∴AC=AD=FA,
∴△DFC是直角三角形,且∠DCF=90°,∠D=30°,
∵BE⊥DC,
∴FC∥BE,
∴△DCF △DEB,
∴ ,
∵BE=3,
∴FC=2,
∴DC= ,
∴ 的面积为 .
故答案为:C.
【分析】先求出△AFC是等边三角形,再求出△DCF △DEB,最后利用锐角三角函数和三角形的面积公式计算求解即可。
9.【答案】 D
【解析】【解答】解: 等边三角形,
,
, ,
,
,
又 ,
,
,
若令 ,则有: ,
由题意只有一个解,
,
解得: ,
故答案为:D.
【分析】先证明 , 再求出 ,最后计算求解即可。
10.【答案】 C
【解析】【解答】解:过点D作DM⊥BC于点M,DN⊥AC于点N,如图所示:
∵ ,CD是 的角平分线, ,
∴ ,
∴ ,
∵ ,
∴△AND∽△DMB,
∵ ,
∴ ,
∴ ,
设 ,则有 ,
∴ ,
∴ ,
∵ ,
∴ ;
故答案为:C.
【分析】过点D作DM⊥BC于点M,DN⊥AC于点N,根据角平分线的性质、正方形的性质及等腰直角三角形的性质证DM=MC=EM=DN=CN,根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似可得△AND∽△DMB,可得比例式= , 设DM=MC=EM=DN=CN=m,则BM=3m,于是结合比例式可将AN、BM用含m的代数式表示出来,由线段的构成BE=BM-EM、AC=AN+CN可将BE、AC用含m的代数式表示出来,根据S1=AC·DN、S2=BE·DM可求解.
11.【答案】 A
【解析】【解答】作点F作FG⊥BC于G,
∵∠DEB+∠FEG=90°,∠DEB+∠BDE=90°;
∴∠BDE=∠FEG,
在△DBE与△EGF中,
,
∴△DBE≌△EGF(AAS),
∴EG=DB,FG=BE=x,
∴EG=DB=2BE=2x,
∴GC=y﹣3x,
∵FG⊥BC,AB⊥BC,
∴FG∥AB,
∴△FGC∽△ABC,
∴CG:BC=FG:AB,
即 = ,
∴y=﹣ .
故答案为:A.
【分析】作点F作FG⊥BC于G,依据已知条件求得△DBE≌△EGF,得出FG=BE=x,EG=DB=2x,然后证得△FGC∽△ABC,再根据相似三角形的性质即可求解.
12.【答案】 D
【解析】【解答】解:∵DE∥AC,
∴△DEO∽△CAO,
∴ =( )2= ,
∴ = ,
∵DE∥AC,
∴△BDE∽△BAC,
∴ =( )2= ,
故答案为:D.
【分析】根据DE∥AC,可证得△DEO∽△CAO,利用现相似三角形的面积比等于相似比的平方,可求出DE与AC的比值;再利用DE∥AC可证得△BDE∽△BAC,利用相似三角形的面积比等于相似比的平方,可求出S△BDE与S△BAC的比.
13.【答案】 C
【解析】【解答】解:∵AD∥BC,EF是梯形ABCD的中位线,
∴EF=(AD+BC),EF∥AD∥BC.
∵BC=3AD,设AD=x,则BC=3AD=3x,EF=2x.
∵EF∥AD,且E、F分别为AB、CD的中点,
∴EG=AD=x,FH=AD=x,
∴GH=x.
∵GH∥BC,
∴△OGH∽△OBC,
∴.
∵△OGH的面积为1,
∴S△OBC=9.
同理△OAD∽△OBC,
∴ ,
∴S△OAD=1.
∵OB=3OD,
∴S△AOB=3S△AOD=3.
∵OC=3OA,
∴S△COD=3S△AOD=3,
∴梯形ABCD的面积=9+1+3+3=16.
故答案为:C.
【分析】根据梯形中位线定理可得EF=(AD+BC),EF∥AD∥BC,根据BC=3AD,设AD=x,则BC=3AD=3x,EF=2x,根据相似三角形面积比等于相似比的平方可得S△OBC=9,根据两个三角形高相等,面积比等于底与底的比可得△AOB和△DOC的面积,进而可得结论.
14.【答案】 D
【解析】【解答】 四边形ABCD是正方形,
,
,
,
,
,
在 和 中, ,
,
,
又 ,
,
,即 ,即结论①符合题意;
在 中, ,
在 中, ,
则 ,结论②不符合题意;
由上已证: ,
,
,
即 ,结论③符合题意;
如图,过点G作 于点H,交AE于点O,则四边形ADGH是矩形,
,
设 ,则 ,
,
,
,
,
,即 ,
解得 ,
,
又 ,
,
,则结论④符合题意;
综上,结论正确的有①③④,
故答案为:D.
【分析】利用正方形的性质,全等三角形的判定与性质,锐角三角函数,相似三角形的性质与判定求解即可。
15.【答案】 A
【解析】【解答】解:(1)∵四边形ABCD和四边形CGEF是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG=90°,
∴△BCE≌△DCG,
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE,
故①正确;
∵△EHG是直角三角形,O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGEF的外接圆上,
∵EF=FG,
∴∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,
∴△EHM∽△GHF,
故②正确;
∵△BGH≌△△EGH,
∴BH=EH,
∵O是EG的中点,
∴HO∥BG,
设EC和OH相交于点N,
∴△DHN∽△DGC,
∴ ,
设HN=a,则BC=2a,
设正方形ECGF的边长是2b,则NC=b,CD=2a,
∴ ,
∴a2+2ab-b2=0,
∴a=(-1+)b或a=(-1-)b(舍去),
∴ ,
∴ ,
故③正确;
∵△BGH≌△EGH,
∴EG=BG,
∵HO是△EBG的中位线,
∴HO=BG,
∴HO=EG,
设正方形ECGF的边长是2b,
∴EG=2b,
∴HO=b,
∵OH∥BG,CG∥EF,
∴OH∥EF,
∴△MHO∽△MFE,
∴ ,
∴EM=OM,
∴ ,
∴ ,
∵EO=GO,
∴S△HOE=S△HOG ,
∴ ,
故④错误.
故答案为:A.
【分析】①先证出△BCE≌△DCG,得出∠BEC=∠BGH,从而∠BEC+∠HDE=90°,即可得出GH⊥BE;
②根据直角三角形斜边的中线等于斜边的一半得出OH=OG=OE,得出点H在正方形CGEF的外接圆上,从而得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,即可证出△EHM∽△GHF;
③先证出△DHN∽△DGC,得出 , 设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,求出a,b的关系,即可求出;
④先证出△MHO∽△MFE,得出 , 从而求出 , 再证出S△HOE=S△HOG , 从而得出 , 即可求解.
16.【答案】 D
【解析】【解答】解:由题意可知:
又∵正方形ABCD中,AB=CB,BG=BG
∴△ABG≌△CBG
∴
又∵点E是BC的中点,
∴CE=BE
又∵正方形ABCD中,AB=CD,
∴△DCE≌△ABE
∴
∵
∴ ,即① 符合题意;
如图:延长DE,AB相交于点M
∵在正方形ABCD中,点E是BC的中点,
∴易证△DCE≌△MBE
∴DC=BM=6
又由① 符合题意
可得
又∵
∴△DCE≌△CBF
∴BF=CE=3
∵DC∥AB
∴△DCH∽△MFH
∴
∴② 符合题意;
由题意可知CE=3,DC=6,∠DCE=90°
∴
又根据三角形面积公式可得:
∴
由△DCE≌△CBF
∴CF=DE
∵DC∥AB
∴△DCG∽△BFG
∴ ,即
∴
∴ ,④符合题意.
过点H作HK⊥AB
由易证可知
∴ ,即
∴
同理: ,即
∴
∴
∴在Rt△AHK中,
∴③ 符合题意;正确的共4个,
故答案为:D.
【分析】根据正方形的性质可先证△ABG≌△CBG,再证△DCE≌△ABE,可得利用余角的性质可证 , 据此判断①;如图:延长DE,AB相交于点M,易证△DCE≌△MBE,可得DC=BM=6,再证△DCE≌△CBF,可得CF=DE.利用平行线可证△DCH∽△MFH,可得∴ , 据此判断②;在Rt△DCE中,利用勾股定理求出DE的长,利用△DCE的面积求出 , 根据平行线可证△DCG∽△BFG,可得 , 从而求出 , 由GH=CG-CH求出GH的长,然后判断④;过点H作HK⊥AB,可得 , , 据此求出HK,FK,从而求出 , 在Rt△AHK中,利用勾股定理求出AH=6,据此判断③.
17.【答案】 B
【解析】【解答】解:由题意可知,OM= ,点N在直线y=-x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,
∴ ON= .
如答图①所示,
设动点P在O点(起点)时,点B的位置为 ,动点P在N点(末点)时,点B的位置为 ,连接 .
∵AO⊥AB0 ,AN⊥ABn ,
∴∠OAC=∠B0ABn.
又∵AB0 =AO tan30°,ABn =AN tan30°,
∴AB0 :AO=ABn :AN=tan30°.
∴△AB0Bn ∽△AON,且相似比为tan30°.
∴ B0Bn =ON tan30°= ×
= .
现在来证明线段 就是点B运动的路径(或轨迹):
如答图②所示,
当点P运动至ON上的任一点时,设其对应的点B为Bi ,连接AP,ABi , B0Bi .
∵AO⊥AB0 ,AP⊥ABi ,
∴∠OAP=∠B0ABi .
又∵AB0 =AO tan30°,A =AP tan30°,
∴AB0 :AO=ABi :AP.
∴△AB0Bi∽△AOP,
∴∠AB0Bi=∠AOP.
又∵△AB0Bn ∽△AON,
∴∠AB0Bn=∠AOP.
∴∠AB0Bi =∠AB0Bn .
∴点Bi在线段B0Bn上,即线段B0Bn 就是点B运动的路径(或轨迹).
综上所述,点B运动的路径(或轨迹)是线段B0Bn,其长度为 .
故答案为:B.
【分析】由题意易证△AB0Bn∽△AON,由相似三角形的性质可得点B的运动路径是线段,且点B的运动路径长为点P运动路径长的倍,然后求出B0Bn的长即可求解.
18.【答案】 D
【解析】【解答】解:如图,作DH⊥AC于H,连接HG延长HG交CD于F,作HE⊥CD于H.
∵DG⊥PG,DH⊥AC,
∴∠DGP=∠DHA,
∵∠DPG=∠DAH,
∴△ADH∽△PDG,
∴ ,∠ADH=∠PDG,
∴∠ADP=∠HDG,
∴△ADP∽△DHG,
∴∠DHG=∠DAP=定值,
∴点G在射线HF上运动,
∴当CG⊥HE时,CG的值最小,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADH+∠HDF=90°,
∵∠DAH+∠ADH=90°,
∴∠HDF=∠DAH=∠DHF,
∴FD=FH,
∵∠FCH+∠CDH=90°,∠FHC+∠FHD=90°,
∴∠FHC=∠FCH,
∴FH=FC=DF=3,
在Rt△ADC中,∵∠ADC=90°,AD=4,CD=3,
∴AC= =5,DH= ,
∴CH= ,
∴EH= ,
∵∠CFG=∠HFE,∠CGF=∠HEF=90°,CF=HF,
∴△CGF≌△HEF(AAS),
∴CG=HE= ,
∴CG的最小值为 ,
故答案为:D.
【分析】如图,作DH⊥AC于H,连接HG延长HG交CD于F,作HE⊥CD于H.证明△ADP∽△DHG,推出∠DHG=∠DAP=定值,推出点G在射线HF上运动,推出当CG⊥HE时,CG的值最小,想办法求出CG即可.
19.【答案】 B
【解析】【解答】解:
∵△ABC∽△ADE,
∴∠ADE=∠ABE,
∴点A,D,B,E四点共圆,
∵∠DAE=90°,
∴∠DBE=90°,
∵F是DE的中点,
∴BF= DE,
∴当DE最小时,BF的值最小,
∵若点E是直线BC上的动点,
∴当AE⊥BC时,AE最小,此时,DE最小,
∵∠BAC=90°,AB=4,AC=3,
∴BC=5,
∴AE= ,
∵△ABC∽△ADE,
∴ ,
∴ ,
∴DE=4,
∴BF=2,
故选B.
【分析】根据相似三角形的性质得到∠ADE=∠ABE,推出点A、D、B、E四点共圆,则得∠DBE=90°,根据直角三角形斜边中线的性质得出BF=DE,则知当DE最小时,BF的值最小,由于当AE⊥BC时,AE最小,得出DE最小,然后根据相似三角形的性质列比例式分别求出AE、DE,即可解答.
20.【答案】 C
【解析】【解答】解:如图1:过E作PQ⊥DC,交DC于P,交AB于Q,连接BE.
∵DC∥AB
∴PQ⊥AB,
∵四边形ABCD是正方形
∴∠ACD=45°
∴△PEC是等腰直角三角形
∴PE=PC.
设PC=x,则PE=x,PD=4-x,EQ=4-x.
∴PD=EQ,
∴∠DPE=∠EQF=90°,∠PED=∠EFQ.
∴△DPE≌△EQF
∴DE=EF
∵DE⊥EF
∴△DEF是等腰直角三角形
易证△DEC≌△BEC
∴DE=BE
∴EF=BE
∵EQ⊥FB
∴FQ=BQ= BF
∵AB=4,F是AB的中点
∴BF=2
∴FQ=BQ=PE=1
∴CE= ,PD=4-1=3
Rt△DAF中,
∴DE=EF=
如图2,
∵DC//AB.
∴△DGC∽△FGA
∴
∴AG=2AG,DG=2FG
∴
∵
∴
∴
连接GM、GN,交EF于H.
∵∠GFE=45°
∴△GHF是等腰直角三角形
∴
由折叠得:GM⊥EF,MH=GH=
∴∠EHM=∠DEF=90°
∴DE∥HM
∴△DEN∽△MNH
∴
∴
∴EN=3NH
∵EN+NH=EH=
∴EN=
∴NH=EH-EN=
在Rt△GNH中,
由折叠得:MN=GN,EM=EG
∴△EMN的周长为 .
故答案为:C.
【分析】如图:过E作PQ⊥DC,交DC于P,交AB于Q,连接BE.先通过等腰三角形和全等三角形的判定和性质得到FQ=BQ=PE=1;再说明△DEF是等腰直角三角形,然后再利用勾股定理计算得到DE=EF= ;如图2,由DC//AB可得△DGC∽△FGA,列比例式可求FG和CG的长,从而得EG的长;然后再根据AGHF是等腰直角三角形,求得GH和FH的长;利用DE∥GM证明△DEN∽△MNH,则 可得EN= ,然后计算出△EMN各边的长,最后求周长即可.
二、填空题
21.【答案】
【解析】【解答】解:连接CB,取BC的中点D,连接DP,AD,
∵圆的半径为2
∴CD=1,CP=2
∴
∵∠PCD=∠BCP,
∴△PCD∽△BCP,
∴ ,
∴PD=BP,
∴AP+BP=AP+PD.
要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,
∴AP+BP最小值为AD的长,
在Rt△ACD中,CD=1,AC=6,
∴ ,
AP+BP的最小值为.
故答案为:.
【分析】连接CB,取BC的中点D,连接DP,AD,可证得CD,CP,CP,CB四条线段成比例,再由∠PCD=∠BCP,可证得△PCD∽△BCP,利用相似三角形的对应边成比例可证得PD=BP,可推出AP+BP=AP+PD;要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,最小值就是线段AD的长;然后在Rt△ACD中,利用勾股定理求出AD的长.
22.【答案】
【解析】【解答】如图所示,作DF⊥AC于F点,
在Rt△ABC中, , ,
根据矩形的性质可得:∠BAC=∠FCD, ,
∴△ABC∽△CFD,
∴ ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
故答案为: .
【分析】作DF⊥AC于F点,根据△ABC∽△CFD,求得CF,OF,再根据平行线分线段成比例定理列式求解即可.
23.【答案】 2或8或5
【解析】【解答】解:∵四边形ABCD是矩形,AD=4,AB=10
∴BC=AD=4,CD=AB=10,
设DP=x,则CP=10-x,
分两种情况进行讨论:
①当△ADP∽△BCP时, ,即
∴ ,
解得: ;
②当△ADP∽△PCB时, ,即 ,
∴
解得:x=2或x=8,
故答案为:2或8或5.
【分析】根据矩形的性质得出对边相等,设DP=x,则CP=10-x,分两种情况进行讨论:即①当△ADP∽△BCP时,②当△ADP∽△PCB时,根据相似三角形的性质分别列方程求解即可.
24.【答案】 1:20
【解析】【解答】解:∵S△BDE:S△DEC=1:4,
∴BE:EC=1:4,
∴BE:BC=1:5,
∵DE∥AC,
∴△BED∽△BCA,
∴ = = ,
设S△BED=k,则S△DEC=4k,S△ABC=25k,
∴S△ADC=20k,
∴S△BDE:S△DCA=1:20.
故答案为:1:20.
【分析】根据相似三角形的判定“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△BED∽△BCA,再由相似三角形的面积的比等于相似比的平方可得可求解.
25.【答案】 (1,0)(3,0)(6,0)
【解析】【解答】设
∵A(2,2),
∴
∴CD=OD=DE=EF=t ,
∵CF∥OB ,
∴△ACF∽△AOB,
∴
∴
要使△BEF与△OFE相似,
∵
∴只要 或
即:BE=2t或 ,
①当BE=2t时,BO=4t ,
∴
∴t1=0(舍去)或 ,
∴B(6,0).
②当 时,
(ⅰ)当B在E的左侧时,
∴
∴t1=0(舍去)或
∴B(1,0).
(ⅱ)当B在E的右侧时,
∴
∴t1=0(舍去)或
∴B(3,0).
综上,B(1,0)(3,0)(6,0).
故答案为(1,0)(3,0)(6,0).
【分析】先证明△ACF∽△AOB,再求出最后分类讨论计算求解即可。
26.【答案】 10
【解析】【解答】解:如图,延长BQ交射线EF于点M,
∵E,F是AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,
∴∠BME=∠MBC,
∵BQ平分∠CBP,
∴∠PBM=∠MBC,
∴∠BME=∠PBM,
∴BP=PM,
∴EP+BP=EM=20,
∵CQ= CE ,
∴ ,
∵EF∥BC,
∴△BCQ∽△MEQ,
∴ = ,
∵EM=20,
∴ ,即BC=10,
故答案为:10.
【分析】延长BQ交射线EF于点M,先证明△BCQ∽△MEQ,然后可得 = ,根据EM=20,即可得出答案.
27.【答案】 或5
【解析】【解答】设BE=x,则EC=10﹣x,
∵△DEF是△DEB折叠所得,
∴EF=BE=x,①当∠CEF=∠B时,
∵△FEC∽△ABC,
∴ ,即 ,
解得x= ;②当∠CEF=∠A时,
∵△ECF∽△ABC,
∴ ,即 ,
解得x=5,
综上,BE= 或5.
【分析】根据折叠与相似三角形的性质,分当∠CEF=∠B时,当∠CEF=∠A时,两种情况进行讨论即可.
28.【答案】 9
【解析】【解答】∵△ABC、△DCE、△GEF都是正三角形
∴△ABC、△DCE、△GEF相似
∴S2:S1=6:4
∴S2= S1=6
∵S3:S2=
∴S3=S2× =9.
故答案为:9
【分析】根据相似三角形对应边成比例求解即可。
29.【答案】
【解析】【解答】解: ,
,
即 ①,
,
,
即 ②,
① ②,
得 ,
,
,
解得 .
故答案为:
【分析】根据相似三角形的性质可得 , , 再将两式相加即可求解。
30.【答案】
【解析】【解答】解:过点 作 于点 ,交 于点 ,如图,
则四边形 为矩形,
, , ,
四边形 是矩形, , ,
, , ,
为 的中点,
,
,
, ,
在 中,由勾股定理得: ,
,
,
,
,
,
,
,
∽ ,
,
,
,
,
,
∽ ,
,
,
.
故答案为:.
【分析】过点F作FH⊥AD于点H,交ED于点O,则四边形ABFH为矩形,由矩形的性质可得AH=BF,FH=AB,EF∥AB,FH=AB=2,BC=AD=3,AD∥BC,由中点的概念可得AE=BE=1,由勾股定理求出AF,根据平行线分线段成比例的性质可得OH、OF,证明△AME∽△FMO,△ADN∽△FBN,由相似三角形的性质可得AM、AN,接下来根据MN=AN-AM进行计算.
31.【答案】 7
【解析】【解答】解:如图,
易得△DEF∽△IGH,
所以 ,
即 ,
解得x1=7,x2=0(舍去).
故答案为:7.
【分析】如图,由正方形和直角三角形的性质可得∠DFE=∠GHI,∠DEF=∠HGI,根据有两个角相等的两个三角形相似可得△DEF∽△IGH,于是可得比例式求解.
32.【答案】 5
【解析】【解答】解:∵AE∥BC
∴△AEG∽△BFG
∴BG:GA=3:1=BF:AE
∵D为AC边上的中点
∴AE:CF=1:1
∴AE=CF
∴BF:AE=(CF+BC):AE=3:1
∴(AE+10):AE=3:1
解得:AE=5.
故答案为:5.
【分析】根据AE∥BC可得△AEG∽△BFG,根据相似三角形的性质可得到AE、BF的关系,再根据D是AC的中点可得AE=CF,进而可求得AE的长.
33.【答案】 1
【解析】【解答】过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F
∴四边形BEFC是梯形
∵G是重心,
∴点D是BC的中点,点G是EF的中点,AG=2DG,
∴DG是梯形BEFC的中位线
∴BE+CF=2DG
∵BE∥AD,CF∥AD
∴
故答案为:1.
【分析】 过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F,易证四边形BEFC是梯形,再利用重心的定义及性质,可得点D是BC的中点,点G是EF的中点,AG=2DG,利用梯形的中位线定理可得到BE+CF=2DG,利用平行线分线段成比例定理可求出的值。
34.【答案】
【解析】【解答】解:过点H作MN∥AD,交AB于M,交CD于N,
∴∠BAD=∠BMN=90°,∠D=∠MNC=90°,
∴四边形ADNM是矩形,
∴AM=DN,MN=AD=2,
∵将△ADE沿AE折叠至△AHE,
∴AH=AD=2,∠AHE=90°,HE=DE=1,
∴∠AHM+∠EHN=90°,且∠MAH+∠AHM=90°,
∴∠MAH=∠EHN,且∠AMH=∠ENH=90°,
∴△AMH∽△HNE,
∴ ,
∴ ,
∴MH=2NE,HN= ,
∵MH+HN=MN=2,
∴2NE+ =2,
∴NE= ,
∴MH= ,HN= ,AM= ,
∴BM= ,
∴BH= ,
∵AB∥CD,
∴ ,
∴NG= ,HG= ,
∴BG= ,EG= ,
∵AB∥CD,
∴ ,即
∴FG= ,
故答案为: .
【分析】过点H作MN∥AD,交AB于M,交CD于N,通过证明△AMH∽△HNE,可得 ,进而得出MH=2EN,HN= ,可求NE的长,即可求BM,MH,HN的长,由平行线分线段成比例可得HG,GN,EG的长,再次利用平行线分线段成比例可得FG的长.
35.【答案】
【解析】【解答】解:延长AD交GB于点M,交BC的延长线于点H,如图所示:
则AH BH,
GE是AB的垂直平分线,
GA= GB,
同理:GD= GC,
在△AGD和△BGC中,
,
△AGD △BGC (SAS),
∠GAD =∠GBC,
在△GAM和△HBM中,
∠GAD =∠GBC,∠GMA= ∠HMB,
∠AGB = ∠AHB = 90°,
∠AGE= ∠AGB= 45°,
∠AGD = ∠BGC,
∠AGB = ∠DGC=90°,
∴△AGB和△DGC是等腰直角三角形,
,
,
又 ∠AGE=∠DGF,
∠AGD=∠EGF,
△AGD △EGF,
.
【分析】延长AD交GB于点M,交BC的延长线于点H,则AH BH,同理:GD= GC,再证明△AGD △BGC (SAS),得出∠GAD =∠GBC,再得出 , 推出 再得出 ,△AGD △EGF,即可得出答案。
36.【答案】
【解析】【解答】解:如图,连接 交 于点 ,作 于点 , 于点 ,
四边形 是矩形,
, ,
,
;
,
;
由折叠得, 垂直平分 ,
,
,
,
,
,
, ;
由 得, ,
解得, ;
, ,
;
,
,
,
,
,
,
,
,
,
,
,
,
,
故答案为: .
【分析】连接BF交CE于点G,作FH⊥BC于点H,PQ⊥BC于点Q,由矩形的性质可得AB=CD=2,∠ABC=∠BCD=90°,由勾股定理求出BD,EC,由折叠的性质可得:CE垂直平分BF,则∠BGC=∠EBC,证明△BGC∽△EBC,根据相似三角形的性质求出GB,进而求出BF、CG的值,根据三角形的面积公式可得FH,证明△CPQ∽△CFH,△BPQ∽△BDC,由相似三角形的性质可得CQ、BQ,据此求解.
37.【答案】 ①②
【解析】【解答】∵AE AD , AD AB ,
∴AE AB .
在Rt△ABE中,∠ABE=90°,cos∠BAE= ,
∴cos∠BAE= .
∴∠BAE=45°,即△ABE是等腰直角三角形.
∵在矩形ABCD中,∠BAD=90°,
∴∠DAF=45°.
∵DF⊥AE ,
∴∠ADF=45°,即△ADF是等腰直角三角形.
∴AD AF .
∴AF=AB .
∵在矩形ABCD中,AB=CD ,
∴AF=CD .故①符合题意;
又∵AF=AB , ∠BAE=45°,
∴∠ABF=67.5°.
∴∠CBG=22.5°.
又∵AE=AD , ∠DAE=45°,
∴∠ADE=67.5°.
∴∠CDE=22.5°.
∴∠CBG=∠CDE .
∵∠C=∠C,
∴△DCE∽△BCG .
∴ .
∵在矩形ABCD中,BC=AD CD ,
∴ .
在△ABF和△ADE中.∠BAF=∠DAE=45°,AF AB ,AE AD ,
∴△ABF∽△ADE .
∴ .
在△ABF和△OEF中,∠OEF=∠ADE=67.5°=∠ABF ,
∵∠AFB=∠OFE , ∠AFB=∠ABF ,
∴△ABF∽△OEF , ∠OEF=∠OFE .
∴OE=OF , ∠EOF=45°.
又∵∠EOF=∠DFO+∠ODF =45°,∠ODF=∠ADE-∠ADF=22.5°,
∴∠ODF =∠DFO .
∴OF OD .
∴OE OF OD DE .
∴ .故②符合题意;
在△BEF和△FDG中, BE =FD , ∠EBF=∠DFG , ∠BEF =∠FDG=∠ADC-∠ADF=45°,
∴△BEF≌△FDG .
连接CF .
又∵ BC=AD AD BE ,
∴ .故③不符合题意;
∵△ABF∽△ADE , △ABF∽△OEF ,
∴△ADE∽△OEF .
在△BEF和△BOE中, ∠BEF ∠BOE 45°,∠EBF ∠OBE ,
∴△BEF∽△BOE .
在△BOE和△DOG中, ∠ODG ∠OBE , ∠BOE ∠DOG ,
∴△BOE∽△DOG .
∴△BEF∽△DOG .
又∵△DCE∽△BCG ,
∴图形中相似三角形超过6对,故④不符合题意.
综上,正确的结论是①②.
故答案为:①②.
【分析】得出△ABE是等腰直角三角形和△ADF是等腰直角三角形,AF=CD .故①符合题意;得出△DCE∽△BCG,即可得出 .故②符合题意;得出△BEF≌△FDG,连接CF,因为BC=AD AD BE , .故③不符合题意;
因为△ABF∽△ADE , △ABF∽△OEF , 得出△ADE∽△OEF,在△BEF和△BOE中,△BEF∽△BOE,在△BOE和△DOG中,△BOE∽△DOG,因为△DCE∽△BCG , 得出图形中相似三角形超过6对,故④不符合题意.
38.【答案】 1;
【解析】【解答】解:①∵AB=3,BC=6, ,
∴ ,
∴ .
又∵PB=PC,
∴ 是等边三角形.
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
∴ ;
②如图,作BC的垂线交BD的延长线于点F,作 于点Q.
∵ ,
∴ ,
∴B、C、F、P四点共圆.
根据所作辅助线可知 ,
∴BF为⊙O直径.
∵ , ,
∴ ,
∴ ,即 .
∴求 的最大值,即PQ最大即可.
根据题意结合图形可知当Q点和O点重合时PQ最大,即最大值为⊙O半径.
∵ ,
∴ ,
∴PQ最大值为 ,
∴ .
故答案为:1, .
【分析】①由题意可求出 ,又可证明 是等边三角形.得出结论 ,从而可求出 ,进而求出 ,最后根据等边三角形“三线合一”即可证明 ,即 ;
②如图,作BC的垂线交BD的延长线于点F,作 于点Q.由圆周角定理可判断B、C、F、P四点共圆,且BF为⊙O直径.又易证 ,得出结论 ,即 .故求PQ最大即可.结合图形可知当Q点和O点重合时PQ最大,且最大值为⊙O半径,即根据含 角的直角三角形的性质结合勾股定理求出半径即可求出 的最大值.
39.【答案】
【解析】【解答】解:由折叠的性质得AE=A'E , 又AE= ,
∴A'E= ,
∵A'E=A'F , ∠EA'B=∠EAB=90°,
∴△A'EF为等腰直角三角形,
∴EF= A'E=2,∠EFC'=45°,
∴AF=AE+EF= +2,△ABF为等腰直角三角形,
∴AB=AF= +2,∠ABF=45°,
∴∠ABE=∠HBF=22.5°,
由折叠的性质得∠C'HF=∠DHF , ∠BHC=∠BHC',
∴∠BHF=∠BHC'+∠C'HF=90°,
∵∠C'FH=∠BFH , ∠BHF=∠FC'H=90°,
∴△FHC'∽△FBH ,
同理△ABE∽△FBH ,
∴△FDH∽△EAB,
∴ ,
∵DH=C'H=CH ,
∴DF= AE= ,
∴AD=AF+DF= +2.
故答案为: +2.
【分析】先求出EF= A'E=2,∠EFC'=45°,再求出△FDH∽△EAB,最后计算求解即可。
40.【答案】 ②③
【解析】【解答】解:∵四边形ABCD为矩形,
∴ ,
∴ ,
由翻折可知: ,
设 ,则 ,
在直角 中, ,
∴ ,
在直角 中,则有 ,
解得: ,
∴ ,
故①不符合题意;
∵四边形ABCD是矩形,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴四边形AFGD是平行四边形,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴②符合题意;
如图,设 ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
在直角 中, ,
在直角 中, ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 时,y由有最小值1,
∴DN的最小值是1,
故③符合题意;
由②可知 ,
∵N不与点G重合,
∴ ,
∴ ,
∴ 为等腰三角形时,
有 或 两种情况,
故④不符合题意.
故答案为:②③.
【分析】设 ,则 ,由勾股定理可求出 ;证出 ,证明 ,由相似三角形的性质可得出 ;设 , ,证明 ,由相似三角形的性质得出 ,可得出y与x的函数关系式,由二次函数的性质可得出答案;由题意可知 , 为等腰三角形,有 或 两种情况.
41.【答案】
【解析】【解答】解:过点N作NG⊥BF于点G , 如图,
∵ 沿 折叠后,点C正好落在 边上的F处,
∴BF=BC=4,
∵四边形ABCD是矩形,
∴AD⊥AD ,
∴∠A=90°,
在Rt△ABF和Rt△GNF中,∠AFB=∠GFN , ∠FAB=∠FGN=90°,
∴△ABF∽△GNF
∴
设GN=x , 则AB=2x ,
∵BM是 的平分线
∴∠ABN=∠GBN ,
在Rt△ABN和Rt△GBN中, ,BN=BN , ∠ABN=∠GBN ,
∴△ABN≌△GBN ,
∴AN=GN=x
∴AF=AN+NF=2+x
在Rt△BAF中,由勾股定理得, ,即:
解得,
∴ ,
故答案为: .
【分析】先证明△ABF∽△GNF,再求出 , 最后计算即可。
42.【答案】 3
【解析】【解答】如图,过点F作FG//BC,交DE于点G,过点M作MH FG,过点N作PN FG,
在矩形 中, ,
,
FG//BC,F是 边的中点,
,
N到FG的距离
,
同理可得,
M到FG的距离 ,
,
故答案为:3.
【分析】如图,过点F作FG//BC,交DE于点G,过点M作MH FG,过点N作PN FG,根据矩形的性质得出 , , 根据三角形中位线定理得出 , 证明 , 可得FG=BE,从而求出N到FG的距离h1= , ,证明 , 由 ,
可求出M到FG的距离 , , 根据计算即可.
43.【答案】
【解析】【解答】解:∵
∴
∴F是BC的中点
∵BD是三角形ABC的中线;
∴点N为三角形ABC的重心,
∴ ,
设FN=k,则AN=2k,AF=3k
过点B作BG//AF交AE的延长线于G,
∴△BGE∽△FAE,
∴
∴BG=1.5k,
∵BG//AF
∴△BGM∽△NAM,
∴
∵
∴
∴
∴
故答案为:
【分析】根据已知 得出F是BC的中点,再结合已知得出点N为三角形ABC的重心,再根据重心的性质以及相似三角形的性质即可得出结论
44.【答案】 b;
【解析】【解答】解:∵D1E1⊥AC , BC⊥AC ,
∴D1E1∥BC ,
∴ ,
∵D1是斜边AB的中点,
∴AD1=BD1 ,
∴ ,
∵AC=b ,
∴AE1=E1C= b ,
∵D1E1∥BC ,
∴ BD1E1与 CD1E1同底同高,面积相等,以此类推;
根据直角三角形的性质以及相似三角形的性质可知:D1E1= BC , CE1= AC , S1= S△ABC;
∴在 ACB中,D2为其重心,
∴D2E1= BE1 ,
∴D2E2= BC , CE2= AC , S2= S△ABC ,
∵D2E2:D1E1=2:3,D1E1:BC=1:2,
∴BC:D2E2=2D1E1: D1E1=3,
∴CD3:CD2=D3E3:D2E2=CE3:CE2=3:4,
∴D3E3= D2E2= × BC= BC , CE3= CE2= × AC= AC , S3= S△ABC…;
∴Sn= S△ABC= × ab= .
故答案为: b , .
【分析】根据直角三角形的性质以及相似三角形的性质,再利用重心可得D2E1= BE1 , 以此类推,得到规律再求解即可。
45.【答案】
【解析】【解答】解:如图,记PE与CD交点为G,
∵四边形PFEC为平行四边形,
∴PF∥CE,
∴∠DPE=∠CEP,∠PDC=∠ECD,
∴△PGD∽△EGC,
∵DF=PD,
∴PD= PF= CE,
∴ ,
∴ ,
∴PE=3PG,
要求PE的最小值,只要求PG的最小值即可,PG的最小值为当PG⊥CD时,
过点C作CH⊥AB于点H,
在Rt△CBH中,∵∠B=60°,BC=5,
∴sin∠B= ,即 ,
∴PG=CH= ,
∴PE=3PG=3× = ,
故答案为: .
【分析】先记PE与CD交点为G,由四边形PCEF为平行四边形和DF=PD以及相似三角形的判定和性质,证得PE=3PG,再根据“垂线段最短”可知当PG⊥CD时PG取得最小值,PE也取得最小值,过点C作CH⊥AB于点H,易证得CH=PG的最小值,由 ∠B=60° , BC=5 ,解直角三角形BHC即可求得CH,进而得到 PE长度的最小值 .
46.【答案】 2
【解析】【解答】解:过Q作QE⊥AB于E,过C作CF⊥AB于F,
∵在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2 ,
∴∠B=30°,
∴AB=2AC=4 ,BC= AC=6,
∵∠AFC=90°,∠A=60°,
∴∠ACF=30°,
∴AF= ,CF=3,
设PF=x,BQ=y,
∴QE= BQ= y,BE= y,
∴PE=3 ﹣ y﹣x,
∵PQ⊥PC,
∴∠PEQ=∠CFP=∠CPQ=90°,
∴∠EQP+∠EPQ=∠EPQ+∠CPF=90°,
∴∠PQE=∠CPF,
∴△PEQ∽△CFP,
∴ ,
∴
∴x2+( y﹣3 )x+ =0,
∵方程有实数解,
∴△≥0,
∴( y﹣3 )2﹣6y≥0,
整理得,y2﹣20y+36≥0,
解得y≤2或y≥18(舍弃),
∴BQ≤2,
∴BQ的最大值为2.
故答案为2.
【分析】过Q作QE⊥AB于E,过C作CF⊥AB于F,利用相似三角形的性质根据一元二次方程,利用根的判别式解决问题即可.
47.【答案】 或 或3
【解析】【解答】解:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=DA=DB,
∴∠ACD=∠DCB=45°,∠DCG=135°,
∵∠EDF=∠EDM=45°,DG=DM,
∴∠ADC=∠MDG,
∴∠ADM=∠CDG,
∴△ADM≌△CDG(SAS),
∴∠DAM=∠DCG=135°,
∵∠CAB=45°,
∴∠CAM=90°,
∴MH=GH= = =5k,
∵∠GDH=∠GAD=45°,∠DGH=∠AGD,
∴△DGH∽△AGD,
∴ = ,
∴DG2=GH GA=40k2 ,
∵AC=BC=6 ,∠ACB=90°,
∴AB= AC=12,
∴AD=CD=6,
∵DJ⊥AC,
∴AJ=JC=3 ,DJ=AJ=IC=3 ,
∴GJ=8K﹣3 ,
在Rt△DJG中,∵DG2=DJ2+GJ2 ,
∴40k2=(8k﹣3 )2+(3 )2 ,
解得k= 或 (舍弃),
∴AH=3k= .
②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:40k2=(8k﹣3 )2+(3 )2 ,
解得k= (舍弃)或 ,
∴AH=3k= .
③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:10k2=(3 ﹣2k)2+(3 )2 ,
解得k= 或﹣3 (舍弃),
∴AH=3k=3 ,
综上所述,满足条件的AH的值为 或 或3 .
故答案为 或 或3 .
【分析】分三种情形:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.首先证明AM⊥AC,利用相似三角形的性质以及勾股定理构建方程解决问题即可.
48.【答案】
【解析】【解答】解:连接CM,过点M作MF⊥BD于点F
∵△ABC为等腰三角形,∠ACB=90°,点M为AB的中点,AB=
∴BM=AB=10 , AC=BC=20,∠CMB=90°,∠BCM=45°
∵CD⊥BN
∴∠CDB=90°
∴∠CDB+∠CMB=180°
∴点C,M,B,D四点共圆
∴∠MDB=∠BCM=45°,∠DCB=∠BMD
∴△DMF为等腰三角形
∵MD=14 , ∴MF=DF=14
在直角三角形BMF中,BF==2
∵cos∠CBN= , ∴BN=25
∴DN=BN-BD=9
∵∠BNE=∠BNA,而∠DCN+∠BNA=90°
∴∠BNE+∠DCN=90°
∴∠BNE=∠DCN
∴∠BNE=∠BMD
∵∠NDE=∠MDB
∴△NDE∽△MDB
∴
解得,NE=
【分析】根据等腰直角三角形的判定以及性质,四点共圆的判定,圆周角的性质,相似三角形的判定和性质进行证明即可得到答案。
49.【答案】 ;x
【解析】【解答】解:(1)∵正方形ABCD的边长为1,BM=x,
∴AM= ,
∵点N是AM的中点,
∴AN= ,
∵EF⊥AM,
∴∠ANE=90°,
∴∠ANE=∠ABM=90°,
∵∠EAN=∠MAB,
∴△AEN∽△AMB,
∴ = ,即 = ,
∴AE= ,
故答案为: ;
( 2 )解:如图,连接AK、MG、CK,
由正方形的轴对称性△ABK≌△CBK,
∴AK=CK,∠KAB=∠KCB,
∵EF⊥AM,N为AM中点,
∴AK=MK,
∴MK=CK,∠KMC=∠KCM,
∴∠KAB=∠KMC,
∵∠KMB+∠KMC=180°,
∴∠KMB+∠KAB=180°,
又∵四边形ABMK的内角和为360°,∠ABM=90°,
∴∠AKM=90°,
在Rt△AKM中,AM为斜边,N为AM的中点,
∴KN= AM=AN,
∴ = ,
∵△AEN∽△AMB,
∴ = =x,
∴ =x,
故答案为:x.
【分析】(1)根据勾股定理求得AM,进而得出AN,证得△AEN∽△AMB,由相似三角形的性质即可求得AE的长;
(2)连接AK、MG、CK,构建全等三角形和直角三角形,证明AK=MK=CK,再根据四边形的内角和定理得∠AKM=90°,利用直角三角形斜边上的中线等于斜边的一半得NK= AM=AN,然后根据相似三角形的性质求得 = =x,即可得出 =x.
50.【答案】
【解析】【解答】解:如图,过D作DG⊥BC于点G,过F作FH⊥DG于点H,
∵tan∠DBC= ,BD=10,设DG=x,BG=2x
∴ ,解得
∴DG= ,BG=
∴GC=BC-BG=
∴CD=
△DCF周长最小,即CF+DF最小
∵∠FDE=90°
∴∠HDF+∠GDE=90°
∵∠GED+∠GDE=90°
∴∠HDF=∠GED
又∵∠DHF=∠EGD=90°
∴△HDF∽△GED
∴
∴FH=2GD=
即F在DG右侧距离 的直线l上运动,如图所示,
作C点关于直线l的对称点C',连接DC',DC'的长即为CF+DF的最小值
∵DG⊥BC,FH⊥DG,FO⊥CC'
∴四边形HFOG为矩形,
∴OG=HF=
又∵GC=
∴OC=OC'=
∴GC'=
在Rt△DGC'中,DC'=
∴△DCF周长的最小值=CD+DC'=
故答案为: .
【分析】过D作DG⊥BC于点G,过F作FH⊥DG于点H,利用tan∠DBC= 和BD=10可求出DG和BG的长,然后求出CD的长,可知△DCF周长最小,即CF+DF最小,利用“一线三垂直”得到△HDF∽△GED,然后根据对应边成比例推出FH=2GD,可知F在DG右侧距离2DG的直线 上,作C点关于直线 的对称点C',连接DC',DC'的长即为CF+DF的最小值,利用勾股定理求出DC',则CD+DC'的长即为周长最小值
一、单选题
1.(2021八下·相城期末)在四边形 中 ,对角线 与 交于 ,过点 作 的平行线,交 、 于 、 .若 , 与 的面积比为 ,则 的长是( )
A. B. C. D.
2.(2021八下·龙口期末)已知点A(0,3),B(-4,3),以原点O为位似中心,把线段AB缩短为原来的 ,其中点C与点A对应,点D与点B对应.则点D的坐标为( )
A. (-1, ) B. (1,- )
C. ( ,-1)或(- ,1) D. (-1, )或(1,- )
3.(2021·玉林模拟)如图,在菱形 中, ,点E,F分别在 , 上,沿 折叠菱形,使点A落在 边上的点G处,且 于点M,若 (取 , ),则 等于( )
A. B. C. D.
4.(2021·东营)如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( )
A. B. C. D.
5.(2021·深圳)在矩形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得 ,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,下列正确的是( )
① ; ② ; ③ ; ④ .
A. 4 B. 3 C. 2 D. 1
6.(2021·安徽模拟)如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( )
A. 1:2 B. 1:3 C. 2:3 D. 3:4
7.(2021·梓潼模拟)如图,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作CD⊥AB,垂足为D,点E为BC的中点,AE与CD交于点F,若DF的长为 ,则AE的长为( )
A. B. 2 C. D. 2
8.(2021·合肥模拟)如图, 中, , ,点 在 的延长线上,且 连接 并延长,过 作 于点 ,若 ,则 的面积为( )
A. 1 B. 2 C. D.
9.(2021·周村模拟)如图,在等边三角形 中, ,点D是边 上一点,且 ,点P是边 上一动点(D,P两点均不与端点重合),作 , 交边 于点E.若 ,当满足条件的点P有且只有一个时,则a的值为( )
A. 4 B. 5 C. D.
10.(2021·杭州)如图,在 中, ,CD是 的角平分线,过点D作 交BC于点E. 和 的面积分别为 和 ,若 ,则 的值为( ).
A. 3 B. C. D.
11.(2021·石家庄月考)如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( )
A. y=﹣ B. y=﹣ C. y=﹣ D. y=﹣
12.(2021·覃塘模拟)如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC, AE、CD相交于点O,若S△DOE:S△COA=1:36,则S△BDE与S△BAC的比是( )
A. 1:3 B. 1:4 C. 1:5 D. 1:36
13.(2021九下·江油开学考)如图,在梯形ABCD中,AD∥BC,BC=3AD,对角线AC、BD交于点O,EF是梯形ABCD的中位线,EF与BD、AC分别交于点G、H,如果△OGH的面积为1,那么梯形ABCD的面积为( )
A. 12 B. 14 C. 16 D. 18
14.(2020九上·揭西期末)如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE、AF于M、N,下列结论:①AF⊥BG;② ;③ ;④ ,其中正确的有( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
15.(2020九上·深圳期末)如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一直线上,顶点B,C,G在同一条直线上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH。以下四个结论:①GH⊥BE;②△EHM∽△FHG;③ ; ,其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
16.(2020九上·福田期中)如图,正方形 的边长为6,点E是 边的中点,连接 与对角线 交于点G,连接 并延长,交 于点F,连接 交 于点H,连接 .以下结论:① ;② ;③ ;④ .其中正确的结论是( )
A. 1 B. 2 C. 3 D. 4
17.(2020九上·邗江月考)如图,已知点A是第一象限内横坐标为2 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长为( ).
A. B. C. 4 D.
18.(2020九上·江苏期中)如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转使∠DPG=∠DAC,且过D作DG⊥PG,连接CG,则CG最小值为( )
A. B. C. D.
19.(2020九上·犍为期中)如图, ∽ , , , ,F是 的中点,若点E是直线 上的动点,连接 ,则 的最小值是( )
A. B. C. D.
20.(2020·昆明模拟)如图,正方形ABCD中, ,点E是对角线AC上一点,连接BE,过点E作 ,交AB于点F,连接DF,交AC于点G,将 沿EF翻折,得到 ,连接DM,交EF于点N,若点F是AB的中点,则 的周长是( )
A. B. C. D.
二、填空题
21.(2021九下·金牛月考)如图,在Rt△ABC中,∠ACB=90°,BC=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP , BP , AP+ =BP的最小值为 .
22.(2021九上·锦州期末)如图,在矩形 中,对角线 , 交于点 ,过点 作 ,交 的延长线于点 ,若 , ,则 的长为________.
23.(2021九上·建湖期末)如图,矩形 中, , , 为 边上的动点,当 时, 与 相似.
24.(2021九上·汝阳期末)如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=________.
25.(2020九上·吉水期末)如图示意图,A点的坐标为(2,2),点C在线段OA上运动(点C不与O、A重合),过点C作CD⊥x轴于D,再以CD为一边在CD右侧画正方形CDEF.连接AF并延长交x轴于B,连接OF.若△BEF与△OEF相似,则点B的坐标是 .
26.(2020九上·龙岗期中)如图,在△ABC中, ,动点P在射线EF上,BP交CE于点D , ∠CBP的平分线交CE于点Q , 当CQ= CE时,EP+BP=20,则BC的长为________.
27.(2020九上·东阿期中)如图,将三角形纸片的一角折叠,使点B落的AC边上的F处,折痕为DE , 已知AB=AC=8,BC=10,若以点E , F , C为顶点的三角形与△ABC相似,那么BE的长是________.
28.(2020九上·青山期中)如图,△ABC、△DCE、△GEF都是正三角形,且B、C、E、F在同一直线上,A、D、G也在同一直线上,设△ABC、△DCE、△GEF的面积分别为S1、S2、S3 . 当S1=4,S2=6时,S3=________.
29.(2020九上·株洲期中)如图, ,点 在 上, 与 交于点 , , ,则 的长为________.
30.(2020九上·织金月考)如图,矩形 的边长 , , 为 的中点, 在边 上,且 , 分别与 、 相交于点 , ,则 的长为 .
31.(2020九上·惠山月考)如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为________.
32.(2020·大通模拟)如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为________.
33.(2020·上城模拟)如图所示,设G是△ABC的重心,过G的直线分别交AB,AC于点P,Q两点,则 =________.
34.(2019·天府新模拟)如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=________.
35.(2021九上·禅城月考)如图,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.若AD、BC所在直线互相垂直, 的值为 .
36.(2021九上·成都开学考)如图,在矩形 中, , ,点 是边 的中点,连接 ,将 沿 折叠得到 , 与 交于点 ,则 的长为 .
37.(2021·牡丹江)如图,矩形ABCD中,AD AB , 点E在BC边上,且AE=AD , DF⊥AE于点F , 连接DE , BF , BF的延长线交DE于点O , 交CD于点G . 以下结论:①AF=DC , ②OF:BF=CE:CG , ③S△BCG S△DFG , ④图形中相似三角形有6对,则正确结论的序号是 .
38.(2021·曾都模拟)如图,在 中, , , , 是 上方一动点,且 , 交 于点E.当点P运动到 时, 的值为 ;随着点P的运动, 的最大值为 .
39.(2021·洪洞模拟)如图,在矩形 中, , 为边 上两点,将矩形 沿 折叠,点 恰好落在 上的 处,且 ,再将矩形 沿过点 的直线折叠,使点 落在 上的 处,折痕交 于点 ,将矩形 再沿 折叠, 与 恰好重合,已知 ,则 .
40.(2021·南沙模拟)如图,在矩形ABCD中,AB=4,AD=5,E是CD边上一点,连结AE , 将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G , 连结DG . 点M、N分别是线段AG , DG上的动点(与端点不重合),且∠DMN=∠DAM , 以下结论:①CE=2;②DM2=DN AF;③DN最小值为1;④若△DMN为等腰三角形,则点M的位置有三种不同情况.其中正确的是 .
41.(2021·周村模拟)如图,在矩形 中, ,E为 上一点,将 沿 折叠,使点C正好落在 边上的F处,作 的平分线交 于N,交 的延长线于M,若 ,则 的长为 .
42.(2021·陕西模拟)已知矩形 , 是 边上一点且 是 边的中点,连接 相交于 两点,则 的面积是 .
43.(2020九上·上海月考)如图, 为 的 边上的点、且 ,中线 被 截得的三线段为 ,则 ________
44.(2020九上·永春期中)如图,已知Rt ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1 , 连结BE1交CD1于D2;过D2作D2E2⊥AC于E2 , 连结BE2交CD1于D3;过D3作D3E3⊥AC于E3 , …,如此继续,可以依次得到点D4 , D5 , …,Dn , 分别记 BD1E1 , BD2E2 , BD3E3 , …, BDnEn的面积为S1 , S2 , S3 , …Sn . 则(1) =________,(2)Sn=________.
45.(2020·西安模拟)如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值________.
46.(2020·青羊模拟)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2 ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为________.
47.(2020·高新模拟)如图,在等腰Rt△ABC中,AC=BC=6 ,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若 = ,则AH的长为________.
48.(2020·哈尔滨模拟)如图所示.△ABC为等腰直角三角形,∠ACB=90°,点M为AB边的中点,点N为射线AC上一点,连接BN,过点C作CD⊥BN于点D。连接MD,作∠BNE=∠BNA,边EN交射线MD于点E,若AB=20 ,MD=14 ,则NE的长为________。
49.(2020九上·丽水期末)如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
( 1 )AE的长为________(用含x的代数式表示);
( 2 )设EK=2KF,则 的值为________.
50.(2020九上·锦江期末)如图,在 中, ,对角线 ,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得 ,连接CF,则 周长的最小值为________.
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】解:∵DC∥AB,
∴△PDC∽△PAB,
∵ ,
∴ ,又AB=2,
∴CD=1,
∵MN∥AB,
∴MN∥CD,
∴△AMP∽△ADC,△BPN∽△BDC,
∴ , ,
∴ , ,
∴MP= ,NP= ,
∴MN=MP+NP= ,
故答案为:C.
【分析】根据平行得到△PDC∽△PAB,可得 ,以及CD=1,再证明△AMP∽△ADC,△BPN∽△BDC,得到 , ,可得MP和NP,从而得到MN.
2.【答案】 D
【解析】【解答】解: 点 , ,以原点 为位似中心,把线段 缩短为原来的 ,得到线段 ,点 与点 对应,
点 的横坐标为: 或 .
点 的纵坐标为: 或 .
所以点D的坐标为(-1, )或(1,- )
故答案为:D.
【分析】根据点的坐标和位似的性质进行求解即可。
3.【答案】 D
【解析】【解答】解:如图,连接AC,交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AO,
∵∠A=60°,
∴∠BAO=30°,
∴AO=AB cos30°= ,
∴AC= ,
∵沿EF折叠菱形,使点A落在BC边上的点G处,
∴EG=AE,
∵EG⊥BD,AC⊥BD,
∴EG∥AC,
∴ ,
又∵EG=AE,
∴ ,
解得AE= ,
∴AE的长为 .
故答案为:D.
【分析】连接AC,交BD于点O,由菱形的性质可得AC⊥BD,AC=2AO,求出∠BAO的度数,表示出AO、AC,由折叠的性质可得:EG=AE,然后根据平行线分线段成比例的性质以及EG=AE可表示出AE.
4.【答案】 A
【解析】【解答】解:设点 的横坐标为 ,
则 、 间的横坐标的差为 , 、 间的横坐标的差为 ,
放大到原来的 倍得到 ,
,
解得: .
故答案为:A.
【分析】设点 的横坐标为 ,根据数轴表示出BC、B'C的横坐标的距离,再根据位似比利时计算即可。
5.【答案】 B
【解析】【解答】
故答案为:① ,①正确;
②∵ , ,
∴ ,
∵ , , ,
∴ ( ),∴ ,∴ ,
∵ , , ,
∴ ( ),∴ ,故②正确;
③∵ , ,∴ ,
∵在 和 中: , ,
∴ ( ),∴ ,
∵ ,∴ ,
又∵ ,
∴ ,∴ ,∴ ,
∵ , ,
∴ ,故③错误;
④由上述可知: , ,∴ ,
∵ ,∴ ,
∴ ,故④正确.
故选B.
【分析】①先证出∠GFB=∠EDC,得出 , 即可判断①正确;
②先证出△DEC≌△FEM,得出EM=EC,从而得出DM=FC,进而证出△DMN≌△FCN,得出MN=NC,即可判断②正确;
③先证出MC∥GE,得出 , 再求出EF,CF的长,得出 , 即可判断③错误;
④先求出BF的长,根据 , 求出GB的长,利用 , 即可判断④正确.
6.【答案】 A
【解析】【解答】 MN是△ABC的中位线
, ,
G是MN的中点
即
又
即:AF:FB .
故答案为:A.
【分析】根据三角形的中位线的性质得到 , 再利用相似三角形的性质和三角形的中位线求出 , 最后整体代入计算即可。
7.【答案】 C
【解析】【解答】解:连接DE,如图所示:
在Rt△ABC中,∠ACB=90°,AC=BC,
∵CD⊥AB,
∴AD=BD,即点D为AB的中点.
∵E为BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,DE= AC,
∴△DEF∽△CAF,
∴DF:CF=DE:AC=1:2,
∴DF= CD= ,
∴CD= .
∴AB=2 .
∵AC=BC,
∴AC2+BC2=2AC2=AB2=8.
∴AC=BC=2.
∴CE=1.
在直角△ACE中,由勾股定理知:
AE= .
故答案为:C.
【分析】连接DE,首先推知ED为△ABC的中位线,然后由中位线的性质得到△DEF∽△CAF,从而求得CD的长度;继而推知AC=BC=2;最后由勾股定理求得AE的长度.
8.【答案】 C
【解析】【解答】解:取AB的中点F,连接CF,
∵∠ACB=90°,∠CBA=30°,
∴∠CAB=60°,FC=FA= AB,
∴△AFC是等边三角形,
∴∠FAC=∠FCA=60°,AC=FC=FA,
∵BA=2AD,
∴AC=AD=FA,
∴△DFC是直角三角形,且∠DCF=90°,∠D=30°,
∵BE⊥DC,
∴FC∥BE,
∴△DCF △DEB,
∴ ,
∵BE=3,
∴FC=2,
∴DC= ,
∴ 的面积为 .
故答案为:C.
【分析】先求出△AFC是等边三角形,再求出△DCF △DEB,最后利用锐角三角函数和三角形的面积公式计算求解即可。
9.【答案】 D
【解析】【解答】解: 等边三角形,
,
, ,
,
,
又 ,
,
,
若令 ,则有: ,
由题意只有一个解,
,
解得: ,
故答案为:D.
【分析】先证明 , 再求出 ,最后计算求解即可。
10.【答案】 C
【解析】【解答】解:过点D作DM⊥BC于点M,DN⊥AC于点N,如图所示:
∵ ,CD是 的角平分线, ,
∴ ,
∴ ,
∵ ,
∴△AND∽△DMB,
∵ ,
∴ ,
∴ ,
设 ,则有 ,
∴ ,
∴ ,
∵ ,
∴ ;
故答案为:C.
【分析】过点D作DM⊥BC于点M,DN⊥AC于点N,根据角平分线的性质、正方形的性质及等腰直角三角形的性质证DM=MC=EM=DN=CN,根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似可得△AND∽△DMB,可得比例式= , 设DM=MC=EM=DN=CN=m,则BM=3m,于是结合比例式可将AN、BM用含m的代数式表示出来,由线段的构成BE=BM-EM、AC=AN+CN可将BE、AC用含m的代数式表示出来,根据S1=AC·DN、S2=BE·DM可求解.
11.【答案】 A
【解析】【解答】作点F作FG⊥BC于G,
∵∠DEB+∠FEG=90°,∠DEB+∠BDE=90°;
∴∠BDE=∠FEG,
在△DBE与△EGF中,
,
∴△DBE≌△EGF(AAS),
∴EG=DB,FG=BE=x,
∴EG=DB=2BE=2x,
∴GC=y﹣3x,
∵FG⊥BC,AB⊥BC,
∴FG∥AB,
∴△FGC∽△ABC,
∴CG:BC=FG:AB,
即 = ,
∴y=﹣ .
故答案为:A.
【分析】作点F作FG⊥BC于G,依据已知条件求得△DBE≌△EGF,得出FG=BE=x,EG=DB=2x,然后证得△FGC∽△ABC,再根据相似三角形的性质即可求解.
12.【答案】 D
【解析】【解答】解:∵DE∥AC,
∴△DEO∽△CAO,
∴ =( )2= ,
∴ = ,
∵DE∥AC,
∴△BDE∽△BAC,
∴ =( )2= ,
故答案为:D.
【分析】根据DE∥AC,可证得△DEO∽△CAO,利用现相似三角形的面积比等于相似比的平方,可求出DE与AC的比值;再利用DE∥AC可证得△BDE∽△BAC,利用相似三角形的面积比等于相似比的平方,可求出S△BDE与S△BAC的比.
13.【答案】 C
【解析】【解答】解:∵AD∥BC,EF是梯形ABCD的中位线,
∴EF=(AD+BC),EF∥AD∥BC.
∵BC=3AD,设AD=x,则BC=3AD=3x,EF=2x.
∵EF∥AD,且E、F分别为AB、CD的中点,
∴EG=AD=x,FH=AD=x,
∴GH=x.
∵GH∥BC,
∴△OGH∽△OBC,
∴.
∵△OGH的面积为1,
∴S△OBC=9.
同理△OAD∽△OBC,
∴ ,
∴S△OAD=1.
∵OB=3OD,
∴S△AOB=3S△AOD=3.
∵OC=3OA,
∴S△COD=3S△AOD=3,
∴梯形ABCD的面积=9+1+3+3=16.
故答案为:C.
【分析】根据梯形中位线定理可得EF=(AD+BC),EF∥AD∥BC,根据BC=3AD,设AD=x,则BC=3AD=3x,EF=2x,根据相似三角形面积比等于相似比的平方可得S△OBC=9,根据两个三角形高相等,面积比等于底与底的比可得△AOB和△DOC的面积,进而可得结论.
14.【答案】 D
【解析】【解答】 四边形ABCD是正方形,
,
,
,
,
,
在 和 中, ,
,
,
又 ,
,
,即 ,即结论①符合题意;
在 中, ,
在 中, ,
则 ,结论②不符合题意;
由上已证: ,
,
,
即 ,结论③符合题意;
如图,过点G作 于点H,交AE于点O,则四边形ADGH是矩形,
,
设 ,则 ,
,
,
,
,
,即 ,
解得 ,
,
又 ,
,
,则结论④符合题意;
综上,结论正确的有①③④,
故答案为:D.
【分析】利用正方形的性质,全等三角形的判定与性质,锐角三角函数,相似三角形的性质与判定求解即可。
15.【答案】 A
【解析】【解答】解:(1)∵四边形ABCD和四边形CGEF是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG=90°,
∴△BCE≌△DCG,
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE,
故①正确;
∵△EHG是直角三角形,O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGEF的外接圆上,
∵EF=FG,
∴∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,
∴△EHM∽△GHF,
故②正确;
∵△BGH≌△△EGH,
∴BH=EH,
∵O是EG的中点,
∴HO∥BG,
设EC和OH相交于点N,
∴△DHN∽△DGC,
∴ ,
设HN=a,则BC=2a,
设正方形ECGF的边长是2b,则NC=b,CD=2a,
∴ ,
∴a2+2ab-b2=0,
∴a=(-1+)b或a=(-1-)b(舍去),
∴ ,
∴ ,
故③正确;
∵△BGH≌△EGH,
∴EG=BG,
∵HO是△EBG的中位线,
∴HO=BG,
∴HO=EG,
设正方形ECGF的边长是2b,
∴EG=2b,
∴HO=b,
∵OH∥BG,CG∥EF,
∴OH∥EF,
∴△MHO∽△MFE,
∴ ,
∴EM=OM,
∴ ,
∴ ,
∵EO=GO,
∴S△HOE=S△HOG ,
∴ ,
故④错误.
故答案为:A.
【分析】①先证出△BCE≌△DCG,得出∠BEC=∠BGH,从而∠BEC+∠HDE=90°,即可得出GH⊥BE;
②根据直角三角形斜边的中线等于斜边的一半得出OH=OG=OE,得出点H在正方形CGEF的外接圆上,从而得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,即可证出△EHM∽△GHF;
③先证出△DHN∽△DGC,得出 , 设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,求出a,b的关系,即可求出;
④先证出△MHO∽△MFE,得出 , 从而求出 , 再证出S△HOE=S△HOG , 从而得出 , 即可求解.
16.【答案】 D
【解析】【解答】解:由题意可知:
又∵正方形ABCD中,AB=CB,BG=BG
∴△ABG≌△CBG
∴
又∵点E是BC的中点,
∴CE=BE
又∵正方形ABCD中,AB=CD,
∴△DCE≌△ABE
∴
∵
∴ ,即① 符合题意;
如图:延长DE,AB相交于点M
∵在正方形ABCD中,点E是BC的中点,
∴易证△DCE≌△MBE
∴DC=BM=6
又由① 符合题意
可得
又∵
∴△DCE≌△CBF
∴BF=CE=3
∵DC∥AB
∴△DCH∽△MFH
∴
∴② 符合题意;
由题意可知CE=3,DC=6,∠DCE=90°
∴
又根据三角形面积公式可得:
∴
由△DCE≌△CBF
∴CF=DE
∵DC∥AB
∴△DCG∽△BFG
∴ ,即
∴
∴ ,④符合题意.
过点H作HK⊥AB
由易证可知
∴ ,即
∴
同理: ,即
∴
∴
∴在Rt△AHK中,
∴③ 符合题意;正确的共4个,
故答案为:D.
【分析】根据正方形的性质可先证△ABG≌△CBG,再证△DCE≌△ABE,可得利用余角的性质可证 , 据此判断①;如图:延长DE,AB相交于点M,易证△DCE≌△MBE,可得DC=BM=6,再证△DCE≌△CBF,可得CF=DE.利用平行线可证△DCH∽△MFH,可得∴ , 据此判断②;在Rt△DCE中,利用勾股定理求出DE的长,利用△DCE的面积求出 , 根据平行线可证△DCG∽△BFG,可得 , 从而求出 , 由GH=CG-CH求出GH的长,然后判断④;过点H作HK⊥AB,可得 , , 据此求出HK,FK,从而求出 , 在Rt△AHK中,利用勾股定理求出AH=6,据此判断③.
17.【答案】 B
【解析】【解答】解:由题意可知,OM= ,点N在直线y=-x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,
∴ ON= .
如答图①所示,
设动点P在O点(起点)时,点B的位置为 ,动点P在N点(末点)时,点B的位置为 ,连接 .
∵AO⊥AB0 ,AN⊥ABn ,
∴∠OAC=∠B0ABn.
又∵AB0 =AO tan30°,ABn =AN tan30°,
∴AB0 :AO=ABn :AN=tan30°.
∴△AB0Bn ∽△AON,且相似比为tan30°.
∴ B0Bn =ON tan30°= ×
= .
现在来证明线段 就是点B运动的路径(或轨迹):
如答图②所示,
当点P运动至ON上的任一点时,设其对应的点B为Bi ,连接AP,ABi , B0Bi .
∵AO⊥AB0 ,AP⊥ABi ,
∴∠OAP=∠B0ABi .
又∵AB0 =AO tan30°,A =AP tan30°,
∴AB0 :AO=ABi :AP.
∴△AB0Bi∽△AOP,
∴∠AB0Bi=∠AOP.
又∵△AB0Bn ∽△AON,
∴∠AB0Bn=∠AOP.
∴∠AB0Bi =∠AB0Bn .
∴点Bi在线段B0Bn上,即线段B0Bn 就是点B运动的路径(或轨迹).
综上所述,点B运动的路径(或轨迹)是线段B0Bn,其长度为 .
故答案为:B.
【分析】由题意易证△AB0Bn∽△AON,由相似三角形的性质可得点B的运动路径是线段,且点B的运动路径长为点P运动路径长的倍,然后求出B0Bn的长即可求解.
18.【答案】 D
【解析】【解答】解:如图,作DH⊥AC于H,连接HG延长HG交CD于F,作HE⊥CD于H.
∵DG⊥PG,DH⊥AC,
∴∠DGP=∠DHA,
∵∠DPG=∠DAH,
∴△ADH∽△PDG,
∴ ,∠ADH=∠PDG,
∴∠ADP=∠HDG,
∴△ADP∽△DHG,
∴∠DHG=∠DAP=定值,
∴点G在射线HF上运动,
∴当CG⊥HE时,CG的值最小,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADH+∠HDF=90°,
∵∠DAH+∠ADH=90°,
∴∠HDF=∠DAH=∠DHF,
∴FD=FH,
∵∠FCH+∠CDH=90°,∠FHC+∠FHD=90°,
∴∠FHC=∠FCH,
∴FH=FC=DF=3,
在Rt△ADC中,∵∠ADC=90°,AD=4,CD=3,
∴AC= =5,DH= ,
∴CH= ,
∴EH= ,
∵∠CFG=∠HFE,∠CGF=∠HEF=90°,CF=HF,
∴△CGF≌△HEF(AAS),
∴CG=HE= ,
∴CG的最小值为 ,
故答案为:D.
【分析】如图,作DH⊥AC于H,连接HG延长HG交CD于F,作HE⊥CD于H.证明△ADP∽△DHG,推出∠DHG=∠DAP=定值,推出点G在射线HF上运动,推出当CG⊥HE时,CG的值最小,想办法求出CG即可.
19.【答案】 B
【解析】【解答】解:
∵△ABC∽△ADE,
∴∠ADE=∠ABE,
∴点A,D,B,E四点共圆,
∵∠DAE=90°,
∴∠DBE=90°,
∵F是DE的中点,
∴BF= DE,
∴当DE最小时,BF的值最小,
∵若点E是直线BC上的动点,
∴当AE⊥BC时,AE最小,此时,DE最小,
∵∠BAC=90°,AB=4,AC=3,
∴BC=5,
∴AE= ,
∵△ABC∽△ADE,
∴ ,
∴ ,
∴DE=4,
∴BF=2,
故选B.
【分析】根据相似三角形的性质得到∠ADE=∠ABE,推出点A、D、B、E四点共圆,则得∠DBE=90°,根据直角三角形斜边中线的性质得出BF=DE,则知当DE最小时,BF的值最小,由于当AE⊥BC时,AE最小,得出DE最小,然后根据相似三角形的性质列比例式分别求出AE、DE,即可解答.
20.【答案】 C
【解析】【解答】解:如图1:过E作PQ⊥DC,交DC于P,交AB于Q,连接BE.
∵DC∥AB
∴PQ⊥AB,
∵四边形ABCD是正方形
∴∠ACD=45°
∴△PEC是等腰直角三角形
∴PE=PC.
设PC=x,则PE=x,PD=4-x,EQ=4-x.
∴PD=EQ,
∴∠DPE=∠EQF=90°,∠PED=∠EFQ.
∴△DPE≌△EQF
∴DE=EF
∵DE⊥EF
∴△DEF是等腰直角三角形
易证△DEC≌△BEC
∴DE=BE
∴EF=BE
∵EQ⊥FB
∴FQ=BQ= BF
∵AB=4,F是AB的中点
∴BF=2
∴FQ=BQ=PE=1
∴CE= ,PD=4-1=3
Rt△DAF中,
∴DE=EF=
如图2,
∵DC//AB.
∴△DGC∽△FGA
∴
∴AG=2AG,DG=2FG
∴
∵
∴
∴
连接GM、GN,交EF于H.
∵∠GFE=45°
∴△GHF是等腰直角三角形
∴
由折叠得:GM⊥EF,MH=GH=
∴∠EHM=∠DEF=90°
∴DE∥HM
∴△DEN∽△MNH
∴
∴
∴EN=3NH
∵EN+NH=EH=
∴EN=
∴NH=EH-EN=
在Rt△GNH中,
由折叠得:MN=GN,EM=EG
∴△EMN的周长为 .
故答案为:C.
【分析】如图:过E作PQ⊥DC,交DC于P,交AB于Q,连接BE.先通过等腰三角形和全等三角形的判定和性质得到FQ=BQ=PE=1;再说明△DEF是等腰直角三角形,然后再利用勾股定理计算得到DE=EF= ;如图2,由DC//AB可得△DGC∽△FGA,列比例式可求FG和CG的长,从而得EG的长;然后再根据AGHF是等腰直角三角形,求得GH和FH的长;利用DE∥GM证明△DEN∽△MNH,则 可得EN= ,然后计算出△EMN各边的长,最后求周长即可.
二、填空题
21.【答案】
【解析】【解答】解:连接CB,取BC的中点D,连接DP,AD,
∵圆的半径为2
∴CD=1,CP=2
∴
∵∠PCD=∠BCP,
∴△PCD∽△BCP,
∴ ,
∴PD=BP,
∴AP+BP=AP+PD.
要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,
∴AP+BP最小值为AD的长,
在Rt△ACD中,CD=1,AC=6,
∴ ,
AP+BP的最小值为.
故答案为:.
【分析】连接CB,取BC的中点D,连接DP,AD,可证得CD,CP,CP,CB四条线段成比例,再由∠PCD=∠BCP,可证得△PCD∽△BCP,利用相似三角形的对应边成比例可证得PD=BP,可推出AP+BP=AP+PD;要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,最小值就是线段AD的长;然后在Rt△ACD中,利用勾股定理求出AD的长.
22.【答案】
【解析】【解答】如图所示,作DF⊥AC于F点,
在Rt△ABC中, , ,
根据矩形的性质可得:∠BAC=∠FCD, ,
∴△ABC∽△CFD,
∴ ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
故答案为: .
【分析】作DF⊥AC于F点,根据△ABC∽△CFD,求得CF,OF,再根据平行线分线段成比例定理列式求解即可.
23.【答案】 2或8或5
【解析】【解答】解:∵四边形ABCD是矩形,AD=4,AB=10
∴BC=AD=4,CD=AB=10,
设DP=x,则CP=10-x,
分两种情况进行讨论:
①当△ADP∽△BCP时, ,即
∴ ,
解得: ;
②当△ADP∽△PCB时, ,即 ,
∴
解得:x=2或x=8,
故答案为:2或8或5.
【分析】根据矩形的性质得出对边相等,设DP=x,则CP=10-x,分两种情况进行讨论:即①当△ADP∽△BCP时,②当△ADP∽△PCB时,根据相似三角形的性质分别列方程求解即可.
24.【答案】 1:20
【解析】【解答】解:∵S△BDE:S△DEC=1:4,
∴BE:EC=1:4,
∴BE:BC=1:5,
∵DE∥AC,
∴△BED∽△BCA,
∴ = = ,
设S△BED=k,则S△DEC=4k,S△ABC=25k,
∴S△ADC=20k,
∴S△BDE:S△DCA=1:20.
故答案为:1:20.
【分析】根据相似三角形的判定“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△BED∽△BCA,再由相似三角形的面积的比等于相似比的平方可得可求解.
25.【答案】 (1,0)(3,0)(6,0)
【解析】【解答】设
∵A(2,2),
∴
∴CD=OD=DE=EF=t ,
∵CF∥OB ,
∴△ACF∽△AOB,
∴
∴
要使△BEF与△OFE相似,
∵
∴只要 或
即:BE=2t或 ,
①当BE=2t时,BO=4t ,
∴
∴t1=0(舍去)或 ,
∴B(6,0).
②当 时,
(ⅰ)当B在E的左侧时,
∴
∴t1=0(舍去)或
∴B(1,0).
(ⅱ)当B在E的右侧时,
∴
∴t1=0(舍去)或
∴B(3,0).
综上,B(1,0)(3,0)(6,0).
故答案为(1,0)(3,0)(6,0).
【分析】先证明△ACF∽△AOB,再求出最后分类讨论计算求解即可。
26.【答案】 10
【解析】【解答】解:如图,延长BQ交射线EF于点M,
∵E,F是AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,
∴∠BME=∠MBC,
∵BQ平分∠CBP,
∴∠PBM=∠MBC,
∴∠BME=∠PBM,
∴BP=PM,
∴EP+BP=EM=20,
∵CQ= CE ,
∴ ,
∵EF∥BC,
∴△BCQ∽△MEQ,
∴ = ,
∵EM=20,
∴ ,即BC=10,
故答案为:10.
【分析】延长BQ交射线EF于点M,先证明△BCQ∽△MEQ,然后可得 = ,根据EM=20,即可得出答案.
27.【答案】 或5
【解析】【解答】设BE=x,则EC=10﹣x,
∵△DEF是△DEB折叠所得,
∴EF=BE=x,①当∠CEF=∠B时,
∵△FEC∽△ABC,
∴ ,即 ,
解得x= ;②当∠CEF=∠A时,
∵△ECF∽△ABC,
∴ ,即 ,
解得x=5,
综上,BE= 或5.
【分析】根据折叠与相似三角形的性质,分当∠CEF=∠B时,当∠CEF=∠A时,两种情况进行讨论即可.
28.【答案】 9
【解析】【解答】∵△ABC、△DCE、△GEF都是正三角形
∴△ABC、△DCE、△GEF相似
∴S2:S1=6:4
∴S2= S1=6
∵S3:S2=
∴S3=S2× =9.
故答案为:9
【分析】根据相似三角形对应边成比例求解即可。
29.【答案】
【解析】【解答】解: ,
,
即 ①,
,
,
即 ②,
① ②,
得 ,
,
,
解得 .
故答案为:
【分析】根据相似三角形的性质可得 , , 再将两式相加即可求解。
30.【答案】
【解析】【解答】解:过点 作 于点 ,交 于点 ,如图,
则四边形 为矩形,
, , ,
四边形 是矩形, , ,
, , ,
为 的中点,
,
,
, ,
在 中,由勾股定理得: ,
,
,
,
,
,
,
,
∽ ,
,
,
,
,
,
∽ ,
,
,
.
故答案为:.
【分析】过点F作FH⊥AD于点H,交ED于点O,则四边形ABFH为矩形,由矩形的性质可得AH=BF,FH=AB,EF∥AB,FH=AB=2,BC=AD=3,AD∥BC,由中点的概念可得AE=BE=1,由勾股定理求出AF,根据平行线分线段成比例的性质可得OH、OF,证明△AME∽△FMO,△ADN∽△FBN,由相似三角形的性质可得AM、AN,接下来根据MN=AN-AM进行计算.
31.【答案】 7
【解析】【解答】解:如图,
易得△DEF∽△IGH,
所以 ,
即 ,
解得x1=7,x2=0(舍去).
故答案为:7.
【分析】如图,由正方形和直角三角形的性质可得∠DFE=∠GHI,∠DEF=∠HGI,根据有两个角相等的两个三角形相似可得△DEF∽△IGH,于是可得比例式求解.
32.【答案】 5
【解析】【解答】解:∵AE∥BC
∴△AEG∽△BFG
∴BG:GA=3:1=BF:AE
∵D为AC边上的中点
∴AE:CF=1:1
∴AE=CF
∴BF:AE=(CF+BC):AE=3:1
∴(AE+10):AE=3:1
解得:AE=5.
故答案为:5.
【分析】根据AE∥BC可得△AEG∽△BFG,根据相似三角形的性质可得到AE、BF的关系,再根据D是AC的中点可得AE=CF,进而可求得AE的长.
33.【答案】 1
【解析】【解答】过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F
∴四边形BEFC是梯形
∵G是重心,
∴点D是BC的中点,点G是EF的中点,AG=2DG,
∴DG是梯形BEFC的中位线
∴BE+CF=2DG
∵BE∥AD,CF∥AD
∴
故答案为:1.
【分析】 过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F,易证四边形BEFC是梯形,再利用重心的定义及性质,可得点D是BC的中点,点G是EF的中点,AG=2DG,利用梯形的中位线定理可得到BE+CF=2DG,利用平行线分线段成比例定理可求出的值。
34.【答案】
【解析】【解答】解:过点H作MN∥AD,交AB于M,交CD于N,
∴∠BAD=∠BMN=90°,∠D=∠MNC=90°,
∴四边形ADNM是矩形,
∴AM=DN,MN=AD=2,
∵将△ADE沿AE折叠至△AHE,
∴AH=AD=2,∠AHE=90°,HE=DE=1,
∴∠AHM+∠EHN=90°,且∠MAH+∠AHM=90°,
∴∠MAH=∠EHN,且∠AMH=∠ENH=90°,
∴△AMH∽△HNE,
∴ ,
∴ ,
∴MH=2NE,HN= ,
∵MH+HN=MN=2,
∴2NE+ =2,
∴NE= ,
∴MH= ,HN= ,AM= ,
∴BM= ,
∴BH= ,
∵AB∥CD,
∴ ,
∴NG= ,HG= ,
∴BG= ,EG= ,
∵AB∥CD,
∴ ,即
∴FG= ,
故答案为: .
【分析】过点H作MN∥AD,交AB于M,交CD于N,通过证明△AMH∽△HNE,可得 ,进而得出MH=2EN,HN= ,可求NE的长,即可求BM,MH,HN的长,由平行线分线段成比例可得HG,GN,EG的长,再次利用平行线分线段成比例可得FG的长.
35.【答案】
【解析】【解答】解:延长AD交GB于点M,交BC的延长线于点H,如图所示:
则AH BH,
GE是AB的垂直平分线,
GA= GB,
同理:GD= GC,
在△AGD和△BGC中,
,
△AGD △BGC (SAS),
∠GAD =∠GBC,
在△GAM和△HBM中,
∠GAD =∠GBC,∠GMA= ∠HMB,
∠AGB = ∠AHB = 90°,
∠AGE= ∠AGB= 45°,
∠AGD = ∠BGC,
∠AGB = ∠DGC=90°,
∴△AGB和△DGC是等腰直角三角形,
,
,
又 ∠AGE=∠DGF,
∠AGD=∠EGF,
△AGD △EGF,
.
【分析】延长AD交GB于点M,交BC的延长线于点H,则AH BH,同理:GD= GC,再证明△AGD △BGC (SAS),得出∠GAD =∠GBC,再得出 , 推出 再得出 ,△AGD △EGF,即可得出答案。
36.【答案】
【解析】【解答】解:如图,连接 交 于点 ,作 于点 , 于点 ,
四边形 是矩形,
, ,
,
;
,
;
由折叠得, 垂直平分 ,
,
,
,
,
,
, ;
由 得, ,
解得, ;
, ,
;
,
,
,
,
,
,
,
,
,
,
,
,
,
故答案为: .
【分析】连接BF交CE于点G,作FH⊥BC于点H,PQ⊥BC于点Q,由矩形的性质可得AB=CD=2,∠ABC=∠BCD=90°,由勾股定理求出BD,EC,由折叠的性质可得:CE垂直平分BF,则∠BGC=∠EBC,证明△BGC∽△EBC,根据相似三角形的性质求出GB,进而求出BF、CG的值,根据三角形的面积公式可得FH,证明△CPQ∽△CFH,△BPQ∽△BDC,由相似三角形的性质可得CQ、BQ,据此求解.
37.【答案】 ①②
【解析】【解答】∵AE AD , AD AB ,
∴AE AB .
在Rt△ABE中,∠ABE=90°,cos∠BAE= ,
∴cos∠BAE= .
∴∠BAE=45°,即△ABE是等腰直角三角形.
∵在矩形ABCD中,∠BAD=90°,
∴∠DAF=45°.
∵DF⊥AE ,
∴∠ADF=45°,即△ADF是等腰直角三角形.
∴AD AF .
∴AF=AB .
∵在矩形ABCD中,AB=CD ,
∴AF=CD .故①符合题意;
又∵AF=AB , ∠BAE=45°,
∴∠ABF=67.5°.
∴∠CBG=22.5°.
又∵AE=AD , ∠DAE=45°,
∴∠ADE=67.5°.
∴∠CDE=22.5°.
∴∠CBG=∠CDE .
∵∠C=∠C,
∴△DCE∽△BCG .
∴ .
∵在矩形ABCD中,BC=AD CD ,
∴ .
在△ABF和△ADE中.∠BAF=∠DAE=45°,AF AB ,AE AD ,
∴△ABF∽△ADE .
∴ .
在△ABF和△OEF中,∠OEF=∠ADE=67.5°=∠ABF ,
∵∠AFB=∠OFE , ∠AFB=∠ABF ,
∴△ABF∽△OEF , ∠OEF=∠OFE .
∴OE=OF , ∠EOF=45°.
又∵∠EOF=∠DFO+∠ODF =45°,∠ODF=∠ADE-∠ADF=22.5°,
∴∠ODF =∠DFO .
∴OF OD .
∴OE OF OD DE .
∴ .故②符合题意;
在△BEF和△FDG中, BE =FD , ∠EBF=∠DFG , ∠BEF =∠FDG=∠ADC-∠ADF=45°,
∴△BEF≌△FDG .
连接CF .
又∵ BC=AD AD BE ,
∴ .故③不符合题意;
∵△ABF∽△ADE , △ABF∽△OEF ,
∴△ADE∽△OEF .
在△BEF和△BOE中, ∠BEF ∠BOE 45°,∠EBF ∠OBE ,
∴△BEF∽△BOE .
在△BOE和△DOG中, ∠ODG ∠OBE , ∠BOE ∠DOG ,
∴△BOE∽△DOG .
∴△BEF∽△DOG .
又∵△DCE∽△BCG ,
∴图形中相似三角形超过6对,故④不符合题意.
综上,正确的结论是①②.
故答案为:①②.
【分析】得出△ABE是等腰直角三角形和△ADF是等腰直角三角形,AF=CD .故①符合题意;得出△DCE∽△BCG,即可得出 .故②符合题意;得出△BEF≌△FDG,连接CF,因为BC=AD AD BE , .故③不符合题意;
因为△ABF∽△ADE , △ABF∽△OEF , 得出△ADE∽△OEF,在△BEF和△BOE中,△BEF∽△BOE,在△BOE和△DOG中,△BOE∽△DOG,因为△DCE∽△BCG , 得出图形中相似三角形超过6对,故④不符合题意.
38.【答案】 1;
【解析】【解答】解:①∵AB=3,BC=6, ,
∴ ,
∴ .
又∵PB=PC,
∴ 是等边三角形.
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
∴ ;
②如图,作BC的垂线交BD的延长线于点F,作 于点Q.
∵ ,
∴ ,
∴B、C、F、P四点共圆.
根据所作辅助线可知 ,
∴BF为⊙O直径.
∵ , ,
∴ ,
∴ ,即 .
∴求 的最大值,即PQ最大即可.
根据题意结合图形可知当Q点和O点重合时PQ最大,即最大值为⊙O半径.
∵ ,
∴ ,
∴PQ最大值为 ,
∴ .
故答案为:1, .
【分析】①由题意可求出 ,又可证明 是等边三角形.得出结论 ,从而可求出 ,进而求出 ,最后根据等边三角形“三线合一”即可证明 ,即 ;
②如图,作BC的垂线交BD的延长线于点F,作 于点Q.由圆周角定理可判断B、C、F、P四点共圆,且BF为⊙O直径.又易证 ,得出结论 ,即 .故求PQ最大即可.结合图形可知当Q点和O点重合时PQ最大,且最大值为⊙O半径,即根据含 角的直角三角形的性质结合勾股定理求出半径即可求出 的最大值.
39.【答案】
【解析】【解答】解:由折叠的性质得AE=A'E , 又AE= ,
∴A'E= ,
∵A'E=A'F , ∠EA'B=∠EAB=90°,
∴△A'EF为等腰直角三角形,
∴EF= A'E=2,∠EFC'=45°,
∴AF=AE+EF= +2,△ABF为等腰直角三角形,
∴AB=AF= +2,∠ABF=45°,
∴∠ABE=∠HBF=22.5°,
由折叠的性质得∠C'HF=∠DHF , ∠BHC=∠BHC',
∴∠BHF=∠BHC'+∠C'HF=90°,
∵∠C'FH=∠BFH , ∠BHF=∠FC'H=90°,
∴△FHC'∽△FBH ,
同理△ABE∽△FBH ,
∴△FDH∽△EAB,
∴ ,
∵DH=C'H=CH ,
∴DF= AE= ,
∴AD=AF+DF= +2.
故答案为: +2.
【分析】先求出EF= A'E=2,∠EFC'=45°,再求出△FDH∽△EAB,最后计算求解即可。
40.【答案】 ②③
【解析】【解答】解:∵四边形ABCD为矩形,
∴ ,
∴ ,
由翻折可知: ,
设 ,则 ,
在直角 中, ,
∴ ,
在直角 中,则有 ,
解得: ,
∴ ,
故①不符合题意;
∵四边形ABCD是矩形,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴四边形AFGD是平行四边形,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴②符合题意;
如图,设 ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
在直角 中, ,
在直角 中, ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 时,y由有最小值1,
∴DN的最小值是1,
故③符合题意;
由②可知 ,
∵N不与点G重合,
∴ ,
∴ ,
∴ 为等腰三角形时,
有 或 两种情况,
故④不符合题意.
故答案为:②③.
【分析】设 ,则 ,由勾股定理可求出 ;证出 ,证明 ,由相似三角形的性质可得出 ;设 , ,证明 ,由相似三角形的性质得出 ,可得出y与x的函数关系式,由二次函数的性质可得出答案;由题意可知 , 为等腰三角形,有 或 两种情况.
41.【答案】
【解析】【解答】解:过点N作NG⊥BF于点G , 如图,
∵ 沿 折叠后,点C正好落在 边上的F处,
∴BF=BC=4,
∵四边形ABCD是矩形,
∴AD⊥AD ,
∴∠A=90°,
在Rt△ABF和Rt△GNF中,∠AFB=∠GFN , ∠FAB=∠FGN=90°,
∴△ABF∽△GNF
∴
设GN=x , 则AB=2x ,
∵BM是 的平分线
∴∠ABN=∠GBN ,
在Rt△ABN和Rt△GBN中, ,BN=BN , ∠ABN=∠GBN ,
∴△ABN≌△GBN ,
∴AN=GN=x
∴AF=AN+NF=2+x
在Rt△BAF中,由勾股定理得, ,即:
解得,
∴ ,
故答案为: .
【分析】先证明△ABF∽△GNF,再求出 , 最后计算即可。
42.【答案】 3
【解析】【解答】如图,过点F作FG//BC,交DE于点G,过点M作MH FG,过点N作PN FG,
在矩形 中, ,
,
FG//BC,F是 边的中点,
,
N到FG的距离
,
同理可得,
M到FG的距离 ,
,
故答案为:3.
【分析】如图,过点F作FG//BC,交DE于点G,过点M作MH FG,过点N作PN FG,根据矩形的性质得出 , , 根据三角形中位线定理得出 , 证明 , 可得FG=BE,从而求出N到FG的距离h1= , ,证明 , 由 ,
可求出M到FG的距离 , , 根据计算即可.
43.【答案】
【解析】【解答】解:∵
∴
∴F是BC的中点
∵BD是三角形ABC的中线;
∴点N为三角形ABC的重心,
∴ ,
设FN=k,则AN=2k,AF=3k
过点B作BG//AF交AE的延长线于G,
∴△BGE∽△FAE,
∴
∴BG=1.5k,
∵BG//AF
∴△BGM∽△NAM,
∴
∵
∴
∴
∴
故答案为:
【分析】根据已知 得出F是BC的中点,再结合已知得出点N为三角形ABC的重心,再根据重心的性质以及相似三角形的性质即可得出结论
44.【答案】 b;
【解析】【解答】解:∵D1E1⊥AC , BC⊥AC ,
∴D1E1∥BC ,
∴ ,
∵D1是斜边AB的中点,
∴AD1=BD1 ,
∴ ,
∵AC=b ,
∴AE1=E1C= b ,
∵D1E1∥BC ,
∴ BD1E1与 CD1E1同底同高,面积相等,以此类推;
根据直角三角形的性质以及相似三角形的性质可知:D1E1= BC , CE1= AC , S1= S△ABC;
∴在 ACB中,D2为其重心,
∴D2E1= BE1 ,
∴D2E2= BC , CE2= AC , S2= S△ABC ,
∵D2E2:D1E1=2:3,D1E1:BC=1:2,
∴BC:D2E2=2D1E1: D1E1=3,
∴CD3:CD2=D3E3:D2E2=CE3:CE2=3:4,
∴D3E3= D2E2= × BC= BC , CE3= CE2= × AC= AC , S3= S△ABC…;
∴Sn= S△ABC= × ab= .
故答案为: b , .
【分析】根据直角三角形的性质以及相似三角形的性质,再利用重心可得D2E1= BE1 , 以此类推,得到规律再求解即可。
45.【答案】
【解析】【解答】解:如图,记PE与CD交点为G,
∵四边形PFEC为平行四边形,
∴PF∥CE,
∴∠DPE=∠CEP,∠PDC=∠ECD,
∴△PGD∽△EGC,
∵DF=PD,
∴PD= PF= CE,
∴ ,
∴ ,
∴PE=3PG,
要求PE的最小值,只要求PG的最小值即可,PG的最小值为当PG⊥CD时,
过点C作CH⊥AB于点H,
在Rt△CBH中,∵∠B=60°,BC=5,
∴sin∠B= ,即 ,
∴PG=CH= ,
∴PE=3PG=3× = ,
故答案为: .
【分析】先记PE与CD交点为G,由四边形PCEF为平行四边形和DF=PD以及相似三角形的判定和性质,证得PE=3PG,再根据“垂线段最短”可知当PG⊥CD时PG取得最小值,PE也取得最小值,过点C作CH⊥AB于点H,易证得CH=PG的最小值,由 ∠B=60° , BC=5 ,解直角三角形BHC即可求得CH,进而得到 PE长度的最小值 .
46.【答案】 2
【解析】【解答】解:过Q作QE⊥AB于E,过C作CF⊥AB于F,
∵在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2 ,
∴∠B=30°,
∴AB=2AC=4 ,BC= AC=6,
∵∠AFC=90°,∠A=60°,
∴∠ACF=30°,
∴AF= ,CF=3,
设PF=x,BQ=y,
∴QE= BQ= y,BE= y,
∴PE=3 ﹣ y﹣x,
∵PQ⊥PC,
∴∠PEQ=∠CFP=∠CPQ=90°,
∴∠EQP+∠EPQ=∠EPQ+∠CPF=90°,
∴∠PQE=∠CPF,
∴△PEQ∽△CFP,
∴ ,
∴
∴x2+( y﹣3 )x+ =0,
∵方程有实数解,
∴△≥0,
∴( y﹣3 )2﹣6y≥0,
整理得,y2﹣20y+36≥0,
解得y≤2或y≥18(舍弃),
∴BQ≤2,
∴BQ的最大值为2.
故答案为2.
【分析】过Q作QE⊥AB于E,过C作CF⊥AB于F,利用相似三角形的性质根据一元二次方程,利用根的判别式解决问题即可.
47.【答案】 或 或3
【解析】【解答】解:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=DA=DB,
∴∠ACD=∠DCB=45°,∠DCG=135°,
∵∠EDF=∠EDM=45°,DG=DM,
∴∠ADC=∠MDG,
∴∠ADM=∠CDG,
∴△ADM≌△CDG(SAS),
∴∠DAM=∠DCG=135°,
∵∠CAB=45°,
∴∠CAM=90°,
∴MH=GH= = =5k,
∵∠GDH=∠GAD=45°,∠DGH=∠AGD,
∴△DGH∽△AGD,
∴ = ,
∴DG2=GH GA=40k2 ,
∵AC=BC=6 ,∠ACB=90°,
∴AB= AC=12,
∴AD=CD=6,
∵DJ⊥AC,
∴AJ=JC=3 ,DJ=AJ=IC=3 ,
∴GJ=8K﹣3 ,
在Rt△DJG中,∵DG2=DJ2+GJ2 ,
∴40k2=(8k﹣3 )2+(3 )2 ,
解得k= 或 (舍弃),
∴AH=3k= .
②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:40k2=(8k﹣3 )2+(3 )2 ,
解得k= (舍弃)或 ,
∴AH=3k= .
③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:10k2=(3 ﹣2k)2+(3 )2 ,
解得k= 或﹣3 (舍弃),
∴AH=3k=3 ,
综上所述,满足条件的AH的值为 或 或3 .
故答案为 或 或3 .
【分析】分三种情形:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.首先证明AM⊥AC,利用相似三角形的性质以及勾股定理构建方程解决问题即可.
48.【答案】
【解析】【解答】解:连接CM,过点M作MF⊥BD于点F
∵△ABC为等腰三角形,∠ACB=90°,点M为AB的中点,AB=
∴BM=AB=10 , AC=BC=20,∠CMB=90°,∠BCM=45°
∵CD⊥BN
∴∠CDB=90°
∴∠CDB+∠CMB=180°
∴点C,M,B,D四点共圆
∴∠MDB=∠BCM=45°,∠DCB=∠BMD
∴△DMF为等腰三角形
∵MD=14 , ∴MF=DF=14
在直角三角形BMF中,BF==2
∵cos∠CBN= , ∴BN=25
∴DN=BN-BD=9
∵∠BNE=∠BNA,而∠DCN+∠BNA=90°
∴∠BNE+∠DCN=90°
∴∠BNE=∠DCN
∴∠BNE=∠BMD
∵∠NDE=∠MDB
∴△NDE∽△MDB
∴
解得,NE=
【分析】根据等腰直角三角形的判定以及性质,四点共圆的判定,圆周角的性质,相似三角形的判定和性质进行证明即可得到答案。
49.【答案】 ;x
【解析】【解答】解:(1)∵正方形ABCD的边长为1,BM=x,
∴AM= ,
∵点N是AM的中点,
∴AN= ,
∵EF⊥AM,
∴∠ANE=90°,
∴∠ANE=∠ABM=90°,
∵∠EAN=∠MAB,
∴△AEN∽△AMB,
∴ = ,即 = ,
∴AE= ,
故答案为: ;
( 2 )解:如图,连接AK、MG、CK,
由正方形的轴对称性△ABK≌△CBK,
∴AK=CK,∠KAB=∠KCB,
∵EF⊥AM,N为AM中点,
∴AK=MK,
∴MK=CK,∠KMC=∠KCM,
∴∠KAB=∠KMC,
∵∠KMB+∠KMC=180°,
∴∠KMB+∠KAB=180°,
又∵四边形ABMK的内角和为360°,∠ABM=90°,
∴∠AKM=90°,
在Rt△AKM中,AM为斜边,N为AM的中点,
∴KN= AM=AN,
∴ = ,
∵△AEN∽△AMB,
∴ = =x,
∴ =x,
故答案为:x.
【分析】(1)根据勾股定理求得AM,进而得出AN,证得△AEN∽△AMB,由相似三角形的性质即可求得AE的长;
(2)连接AK、MG、CK,构建全等三角形和直角三角形,证明AK=MK=CK,再根据四边形的内角和定理得∠AKM=90°,利用直角三角形斜边上的中线等于斜边的一半得NK= AM=AN,然后根据相似三角形的性质求得 = =x,即可得出 =x.
50.【答案】
【解析】【解答】解:如图,过D作DG⊥BC于点G,过F作FH⊥DG于点H,
∵tan∠DBC= ,BD=10,设DG=x,BG=2x
∴ ,解得
∴DG= ,BG=
∴GC=BC-BG=
∴CD=
△DCF周长最小,即CF+DF最小
∵∠FDE=90°
∴∠HDF+∠GDE=90°
∵∠GED+∠GDE=90°
∴∠HDF=∠GED
又∵∠DHF=∠EGD=90°
∴△HDF∽△GED
∴
∴FH=2GD=
即F在DG右侧距离 的直线l上运动,如图所示,
作C点关于直线l的对称点C',连接DC',DC'的长即为CF+DF的最小值
∵DG⊥BC,FH⊥DG,FO⊥CC'
∴四边形HFOG为矩形,
∴OG=HF=
又∵GC=
∴OC=OC'=
∴GC'=
在Rt△DGC'中,DC'=
∴△DCF周长的最小值=CD+DC'=
故答案为: .
【分析】过D作DG⊥BC于点G,过F作FH⊥DG于点H,利用tan∠DBC= 和BD=10可求出DG和BG的长,然后求出CD的长,可知△DCF周长最小,即CF+DF最小,利用“一线三垂直”得到△HDF∽△GED,然后根据对应边成比例推出FH=2GD,可知F在DG右侧距离2DG的直线 上,作C点关于直线 的对称点C',连接DC',DC'的长即为CF+DF的最小值,利用勾股定理求出DC',则CD+DC'的长即为周长最小值
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
