2021--2022学年人教版八年级数学上册13.3.1等腰三角形的性质 第1课时 学案
文档属性
| 名称 | 2021--2022学年人教版八年级数学上册13.3.1等腰三角形的性质 第1课时 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 90.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览


文档简介
“学讲清”教学案
学科 数学 年级 八年级 主备人 审核人 时间: 2021 年11 月 04 日
课题 13.3.1第1课时 等腰三角形的性质 课型 新授课 课时 执教教师 孙明靖
学习 目标 1.理解并掌握等腰三角形的性质. 2.经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
学习 重点 难点 重点:掌握等腰三角形的性质 难点:运用等腰三角形的性质解决有关问题.
学习 环节 学习内容 活动与评价
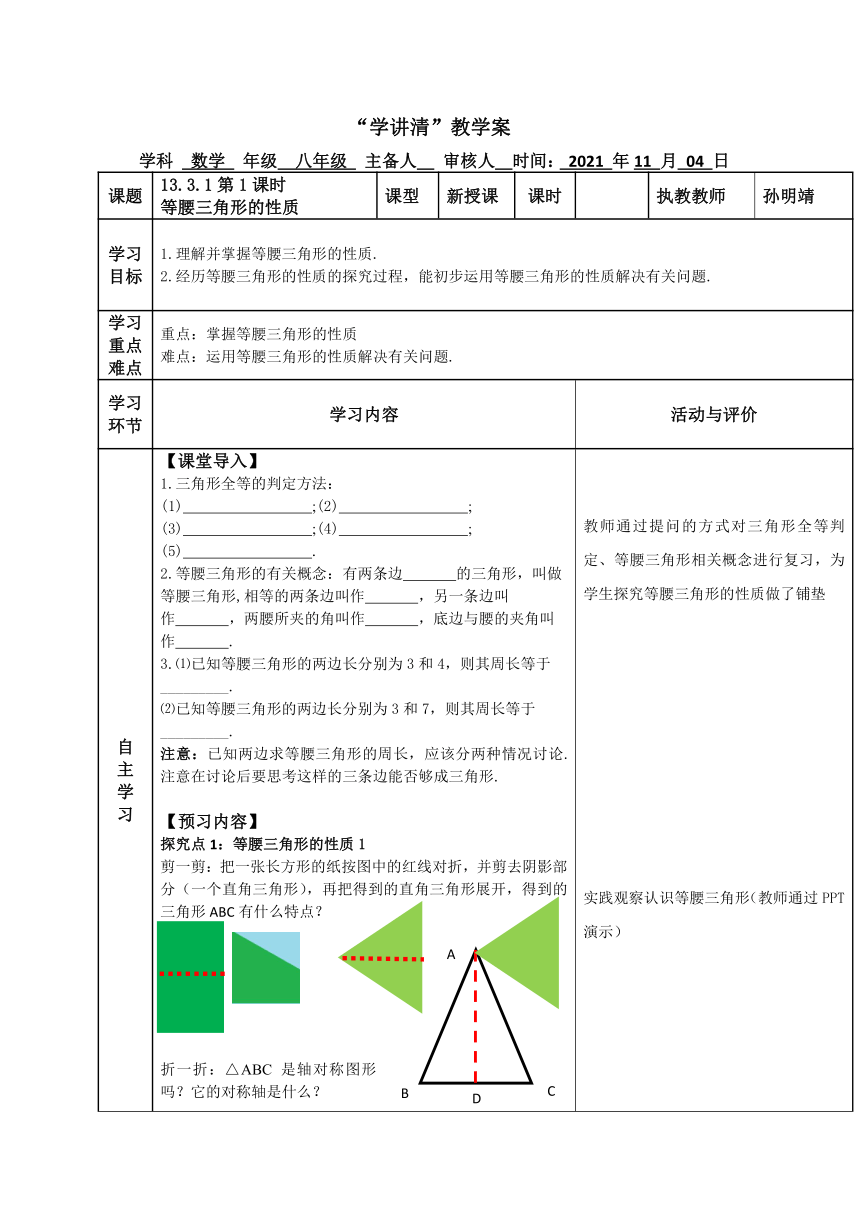
自 主 学 习 【课堂导入】 1.三角形全等的判定方法:(1) ;(2) ; (3) ;(4) ; (5) . 2.等腰三角形的有关概念:有两条边 的三角形,叫做等腰三角形,相等的两条边叫作 ,另一条边叫作 ,两腰所夹的角叫作 ,底边与腰的夹角叫作 . 3.⑴已知等腰三角形的两边长分别为3和4,则其周长等于_________. ⑵已知等腰三角形的两边长分别为3和7,则其周长等于_________. 注意:已知两边求等腰三角形的周长,应该分两种情况讨论.注意在讨论后要思考这样的三条边能否够成三角形. 【预习内容】 探究点1:等腰三角形的性质1 剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点? 折一折:△ABC 是轴对称图形吗?它的对称轴是什么? 找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角. 重合的线段重合的角
猜一猜: 由这些重合的角,你能发现等腰三角形的什么性质吗?说一说你的猜想. 要点归纳:性质1 等腰三角形的两个底角 (等边对等角). 证一证:请用学过的知识证明你的猜想.你有哪些证明方法? 已知:如图,△ABC 中,AB=AC. 求证:∠B=∠C . 典例精析 例1:如图,在△ABC中,AB=AD=DC,∠BAD=26°,求 ∠B和∠C的度数. 方法总结:利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小角的度数为x. 例2:等腰三角形的一个内角是50°,则这个三角形的底角的大小是( ) A.65°或50° B.80°或40° C.65°或80° D.50°或80° 方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论. 教师通过提问的方式对三角形全等判定、等腰三角形相关概念进行复习,为学生探究等腰三角形的性质做了铺垫 实践观察认识等腰三角形(教师通过PPT演示) 教师提问:观察表格,等腰三角形除了两腰相等以外,你还能发现其他性质吗? 学生通过观察,独立完成表格,然后小组讨论交流,猜想论证:等腰三角形的两个底角相等。 教师引导学生多角度、多方法解决问题。(学生主要从作底边上的中线、底边上的高、顶角的平分线思考) 通过练习,进一步巩固等腰三角形的性质
精 讲 点 拨 【合作探究】 探究点2:三角形的性质2 问题1:由折叠后的三角形得到的重合线段,你能发现等腰三角形的什么性质吗?说一说你的猜想. 要点归纳:性质2 等腰三角形的 , , 互相重合填一填:填空:如图①,在△ABC中, ∵AB=AC,∠BAD=∠CAD,∴BD = , ⊥ . ∵AB=AC,BD=CD,∴∠BAD= , ⊥ . ∵AB=AC,AD⊥BC,∴∠BAD= , BD= . 想一想:画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合? 【延伸拓展】 例3:已知点D、E在△ABC的边BC上,AB=AC. (1)如图①,若AD=AE,求证:BD=CE; (2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC. 方法总结:(通常说成等腰三角形的“三线合一”). 【课堂小结】 等腰三角形的性质内容主要事项性质1等边对等角注意分类讨论; 求角度时可结合方程思想性质2三线合一三线指的是顶角的平分线、底边上的中线及底边上的高.腰上的高和中线与底角的平分线不具有这一性质.
得出性质1后,教师及时引导学生通过对等腰三角形轴对称形的研究和从拼图、剪纸活动中获得感悟,猜想并证明性质2 学生归纳总结得出性质2 学生独立思考,教师关注学生是否能够正确理解性质2
达 标 检 测 1.等腰三角形有一个角是90°,则另两个角分别是( ) A.30°,60° B.45°,45° C.45°,90° D.20°,70° 如图,在△ABC中,AB=AC,过点A作AD∥ BC,若∠1=70°则∠BAC的大小为( ) A.40° B.30° C.70° D.50° 3.(1)等腰三角形一个底角为75°,它的另外两个角为______; (2)等腰三角形一个角为36°,它的另外两个角为____________________; (3)等腰三角形一个角为120°,它的另外两个角为_____. 4.在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底 角的大小为___________.
板 书 设 计 13.3.1 等腰三角形(第1课时) 一、定义 二、等腰三角形的性质 性质1: 等边对等角 性质2: 三线合一例题 变式
课 后 反 思
学科 数学 年级 八年级 主备人 审核人 时间: 2021 年11 月 04 日
课题 13.3.1第1课时 等腰三角形的性质 课型 新授课 课时 执教教师 孙明靖
学习 目标 1.理解并掌握等腰三角形的性质. 2.经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
学习 重点 难点 重点:掌握等腰三角形的性质 难点:运用等腰三角形的性质解决有关问题.
学习 环节 学习内容 活动与评价
自 主 学 习 【课堂导入】 1.三角形全等的判定方法:(1) ;(2) ; (3) ;(4) ; (5) . 2.等腰三角形的有关概念:有两条边 的三角形,叫做等腰三角形,相等的两条边叫作 ,另一条边叫作 ,两腰所夹的角叫作 ,底边与腰的夹角叫作 . 3.⑴已知等腰三角形的两边长分别为3和4,则其周长等于_________. ⑵已知等腰三角形的两边长分别为3和7,则其周长等于_________. 注意:已知两边求等腰三角形的周长,应该分两种情况讨论.注意在讨论后要思考这样的三条边能否够成三角形. 【预习内容】 探究点1:等腰三角形的性质1 剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点? 折一折:△ABC 是轴对称图形吗?它的对称轴是什么? 找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角. 重合的线段重合的角
猜一猜: 由这些重合的角,你能发现等腰三角形的什么性质吗?说一说你的猜想. 要点归纳:性质1 等腰三角形的两个底角 (等边对等角). 证一证:请用学过的知识证明你的猜想.你有哪些证明方法? 已知:如图,△ABC 中,AB=AC. 求证:∠B=∠C . 典例精析 例1:如图,在△ABC中,AB=AD=DC,∠BAD=26°,求 ∠B和∠C的度数. 方法总结:利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小角的度数为x. 例2:等腰三角形的一个内角是50°,则这个三角形的底角的大小是( ) A.65°或50° B.80°或40° C.65°或80° D.50°或80° 方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论. 教师通过提问的方式对三角形全等判定、等腰三角形相关概念进行复习,为学生探究等腰三角形的性质做了铺垫 实践观察认识等腰三角形(教师通过PPT演示) 教师提问:观察表格,等腰三角形除了两腰相等以外,你还能发现其他性质吗? 学生通过观察,独立完成表格,然后小组讨论交流,猜想论证:等腰三角形的两个底角相等。 教师引导学生多角度、多方法解决问题。(学生主要从作底边上的中线、底边上的高、顶角的平分线思考) 通过练习,进一步巩固等腰三角形的性质
精 讲 点 拨 【合作探究】 探究点2:三角形的性质2 问题1:由折叠后的三角形得到的重合线段,你能发现等腰三角形的什么性质吗?说一说你的猜想. 要点归纳:性质2 等腰三角形的 , , 互相重合填一填:填空:如图①,在△ABC中, ∵AB=AC,∠BAD=∠CAD,∴BD = , ⊥ . ∵AB=AC,BD=CD,∴∠BAD= , ⊥ . ∵AB=AC,AD⊥BC,∴∠BAD= , BD= . 想一想:画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合? 【延伸拓展】 例3:已知点D、E在△ABC的边BC上,AB=AC. (1)如图①,若AD=AE,求证:BD=CE; (2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC. 方法总结:(通常说成等腰三角形的“三线合一”). 【课堂小结】 等腰三角形的性质内容主要事项性质1等边对等角注意分类讨论; 求角度时可结合方程思想性质2三线合一三线指的是顶角的平分线、底边上的中线及底边上的高.腰上的高和中线与底角的平分线不具有这一性质.
得出性质1后,教师及时引导学生通过对等腰三角形轴对称形的研究和从拼图、剪纸活动中获得感悟,猜想并证明性质2 学生归纳总结得出性质2 学生独立思考,教师关注学生是否能够正确理解性质2
达 标 检 测 1.等腰三角形有一个角是90°,则另两个角分别是( ) A.30°,60° B.45°,45° C.45°,90° D.20°,70° 如图,在△ABC中,AB=AC,过点A作AD∥ BC,若∠1=70°则∠BAC的大小为( ) A.40° B.30° C.70° D.50° 3.(1)等腰三角形一个底角为75°,它的另外两个角为______; (2)等腰三角形一个角为36°,它的另外两个角为____________________; (3)等腰三角形一个角为120°,它的另外两个角为_____. 4.在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底 角的大小为___________.
板 书 设 计 13.3.1 等腰三角形(第1课时) 一、定义 二、等腰三角形的性质 性质1: 等边对等角 性质2: 三线合一例题 变式
课 后 反 思
