2021-2022学年沪科版九年级数学上册 23.2 解直角三角的应用 教案
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册 23.2 解直角三角的应用 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 63.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 11:10:23 | ||
图片预览


文档简介
教学设计
课题 23.2 解直角三角的应用
学科(版本) 沪科版 章节 第二节第二课时
学时 1 课时 年级 九年级
教材分析 本节课位于沪科版数学九年级上册第 23 章第二节第 2 课时,它是学生在学习了锐角三角函数及解直角三角形意义的基础上编排的,应用三角函数知识,解决实际问题中的测量问题,主要应让学生学会用直角三角形的有关知识去解决某些简单的实际问题。它既是前面所学知识的运用,也是高中继续解斜三角形的重要预备知识。它的学习还蕴涵着深刻的数学思想方法(数学建模、转化化归),因此,本节课内容对于培养学生的应用意识和分析、解决问题的能力有重要的作用.
学情分析 在此之前,学生已经熟练掌握了锐角三角函数关系式,并能够选择适当的三角函数关系解直角三角形,但对于本节课,如何把实际问题转化为数学问题,抽象出直角三角形去解,学生会感到困难.
教学目标 知识与技能:使学生掌握仰角、俯角的概念,并学会正确运用这些概念和解直角三角形的知识解决一些实际问题. 过程与方法:让学生体验方程思想和数学结合思想在解直角三角形中的用 途. 情感与态度:使学生感知本节课与现实生活的密切联系,进一步认识到数学知识运用于实践的意义.
教学重点难点以及措施 会利用解直角三角形的知识解决与仰角、俯角有关的实际问题. 通过构造直角三角形,把实际问题转化为数学问题.
教学环节 教学内容 设计意图 活动目标 信息技术使用及分 析
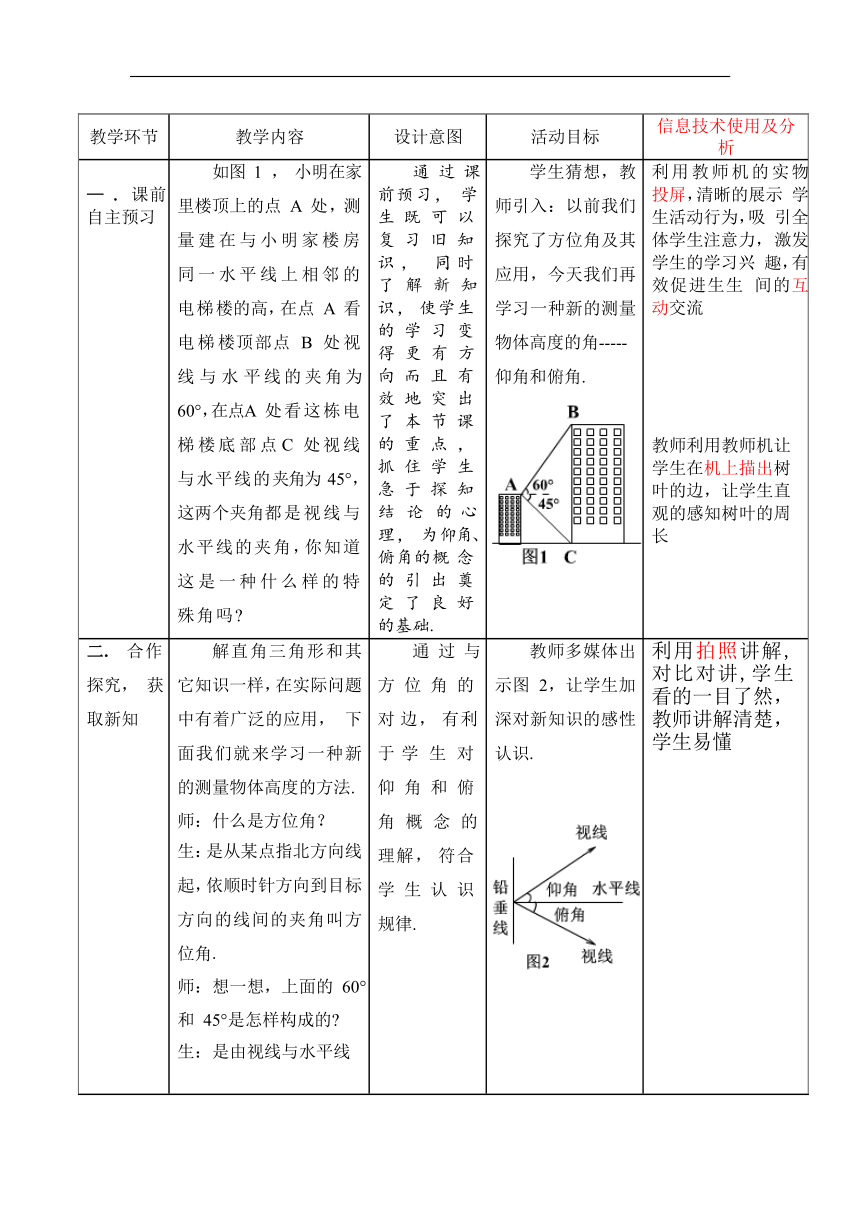
— . 课前自主预习 如图 1 , 小明在家里楼顶上的点 A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点 A 看电梯楼顶部点 B 处视线与水平线的夹角为 60°,在点A 处看这栋电梯楼底部点 C 处视线与水平线的夹角为 45°,这两个夹角都是视线与水平线的夹角,你知道这是一种什么样的特殊角吗 通 过 课前预习, 学生既可以复习旧知识, 同时了解新知识, 使学生的学习变得更有方向而且有效地突出了本节课的重点, 抓住学生急于探知结论的心理, 为仰角、俯角的概念的引出奠定了良好的基础. 学生猜想,教师引入:以前我们探究了方位角及其应用,今天我们再学习一种新的测量物体高度的角----- 仰角和俯角. 利用教师机的实物 投屏,清晰的展示 学生活动行为,吸 引全体学生注意力, 激发学生的学习兴 趣,有效促进生生 间的互动交流 教师利用教师机让学生在机上描出树叶的边,让学生直观的感知树叶的周长
二. 合作探究, 获取新知 解直角三角形和其它知识一样,在实际问题中有着广泛的应用, 下面我们就来学习一种新的测量物体高度的方法. 师:什么是方位角? 生:是从某点指北方向线起,依顺时针方向到目标方向的线间的夹角叫方位角. 师:想一想,上面的 60° 和 45°是怎样构成的 生:是由视线与水平线 通 过 与方位角的对边, 有利于学生对仰角和俯角概念的理解, 符合学生认识规律. 教师多媒体出示图 2,让学生加深对新知识的感性认识. 利用拍照讲解, 对比对讲,学生看的一目了然, 教师讲解清楚, 学生易懂
组成的角. 师:请同学们归纳下仰角、俯角的概念 生:在进行测量时,由 视线与水平线的夹角中视线在水平线的上方, 视线与水平线的夹角叫仰角,视线在水平线下方,视线与水平线的夹角叫俯角.
三、学以致用, 加深认识 例 1 如图 3 , 学生要测量校园内一颗水杉树的高度,他站在距离水杉树 8m 的 E 处, 测得树顶 的 仰 角 为 ∠ACD=52° , 已知测角器的高度 CE=1.6m , 问树高 AB 为多少米?(精确到 0.1m) 解:在 Rt△ADC 中 ∵∠ACD=50° , CD=BE =8m 又∵tan∠ACD= ∴AD=CD·tan∠ACD =8×tan52° =8×1.2799 ≈10.2(m) ∵DB=CE=1.6m ∴AB=AD+BD=10.2+1.6 通 过 对例题的解答加深了学生对仰角、俯角意义的理解并能熟练加以运用. 想一想:在这个图中, 52° 的仰角指的是哪个角? 议一议:水杉 树的高度可分成几 个部分?如何求解? 学生独立完成 然后同桌交流,代表展示,师生共同纠正. 教师多媒体展 示解题过程,规范 学生的解题步骤. 老师的提问可以设置抢答、随机作答和小组讨论作答 以选择题、判断, 填空题或者主观题等任何形式推送到学生端,这题利用判断的形式学生选 ,择正确的答案,或 者把自己写在纸上的答案拍照上传给老师,老师第一时间看到谁上交了、谁没交,选择题直接出正答率,或者抽取学生有代表性的答案进行点评.
=11.8(m) 答:树高AB 为 11.8m.
四. 探究新知 例 2 如图 4 , 某校九年级学生要测量当地电视塔的高度 AB, 因为不能直接到达塔底 B 处他们采用在发射台院外与电视塔成一直线的C、D 两处的地面上,用测角器测得电视塔顶部A 的仰角分别为 45° 和30° , 同时量得 CD 为 50m, 已知测角器高为 1m,问电视塔的高度为多少米?(精确到 1m). 解:设 AB1=xm. 在 Rt△AC1B1 中, 由 ∠ AC1B1=45° , 得 C1B1=AB1=x 在 Rt△AD1B1 中, 由∠AD1B1=30°,得tan∠AD1B1== 即 3 x 3 50 x 解 方 程 , 得 x=25(+1)≈68 让 学 生经历利用仰角、俯角测量 ,不 可以到达底部的物体高度的探究过程, 增强直角三角形的边角关系在物体高度测量问题中的应用, 进一步提高学生的建模思想及把实际问题转化成数学问题的能力. 想一想:在图中 , 仰 角 45° 和30° 分别指哪两个角? 观察思考:图 中有几个直角三角形?你能得出哪些结论? 议一议:此题 的等量关系是什么电视塔的高度包括几部分? 学生交流讨论 回答问题,然后独立完成后,与同桌交流,代表展示, 师生共同纠正. 利用教师机拍照讲解,对比对讲, 也可利用相机功能让所有学生看的清楚听的明白 ,
∴AB=AB1+B1B≈68+1=6 9(m). 答: 电视塔的高度为 69m.
五.变式训 练 如图 6 , 某直升机于空中 A 处测得正前方地面控制点 C 的俯角为30°;若航向不变,直升机继续向前飞行 1000m 至 B 处,测得地面控制点 C 的俯角为 45°.求直升机再向前飞行多远, 与地面控制点 C 的距离最近(结果保留根号) 设 计 练习是由易到难进行设计的, 目的是除了培养学生一般思维品质的基础外, 还要有意识的培养学生思维的创新。 学生独立完成一名学生演示,其余下面完成,教师巡视,帮助学困生然后集体纠正. 以选择题、判断,填 ,空题或者主观题等 任何形式推送到学 生端,这些题利用 判断的形式,拍照 的形式学生选择正 确的答案,或者把 自己写在纸上的答 案拍照上传给老师, 老师第一时间看到 谁上交了、谁没交, 抽取学生有代表性 的答案进行点评.
六. 思维拓展 如图 5 , 小明在家里楼顶上的点 A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点 A 看电梯楼顶部点 B 处仰角为60°,在点A 处看这栋电梯楼底部点 C 处俯角为45°,两栋楼之间的距离 30m, 求电梯楼 BC 的高 (结果保留根号). 通 过 练习加深对仰角、俯角的理解, 培养学生合作学习的能力, 让学生树立解决问题的信心, 进一步巩固三角函数在解直角三角形中的 应用技巧及 小组合作完成代表展示,教师巡视,帮助学困生, 然后集体纠正. ,
方法, 提高解决问题的综合能力.
七.课 堂 小结 八. 布置作业 通过本节课学习,我们学习了哪些内容? 学生归纳,教师点评: 仰角、俯角概念; 利用仰角、俯角解决实际问题的方法. 【设计意图】通过课堂小结的形式,帮助学生养成整理知识的习惯,加深认识深化提高,形成体系,同时明确学习重点. 教科书 P131 页习题 23.2 第 2,3 题.
课题 23.2 解直角三角的应用
学科(版本) 沪科版 章节 第二节第二课时
学时 1 课时 年级 九年级
教材分析 本节课位于沪科版数学九年级上册第 23 章第二节第 2 课时,它是学生在学习了锐角三角函数及解直角三角形意义的基础上编排的,应用三角函数知识,解决实际问题中的测量问题,主要应让学生学会用直角三角形的有关知识去解决某些简单的实际问题。它既是前面所学知识的运用,也是高中继续解斜三角形的重要预备知识。它的学习还蕴涵着深刻的数学思想方法(数学建模、转化化归),因此,本节课内容对于培养学生的应用意识和分析、解决问题的能力有重要的作用.
学情分析 在此之前,学生已经熟练掌握了锐角三角函数关系式,并能够选择适当的三角函数关系解直角三角形,但对于本节课,如何把实际问题转化为数学问题,抽象出直角三角形去解,学生会感到困难.
教学目标 知识与技能:使学生掌握仰角、俯角的概念,并学会正确运用这些概念和解直角三角形的知识解决一些实际问题. 过程与方法:让学生体验方程思想和数学结合思想在解直角三角形中的用 途. 情感与态度:使学生感知本节课与现实生活的密切联系,进一步认识到数学知识运用于实践的意义.
教学重点难点以及措施 会利用解直角三角形的知识解决与仰角、俯角有关的实际问题. 通过构造直角三角形,把实际问题转化为数学问题.
教学环节 教学内容 设计意图 活动目标 信息技术使用及分 析
— . 课前自主预习 如图 1 , 小明在家里楼顶上的点 A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点 A 看电梯楼顶部点 B 处视线与水平线的夹角为 60°,在点A 处看这栋电梯楼底部点 C 处视线与水平线的夹角为 45°,这两个夹角都是视线与水平线的夹角,你知道这是一种什么样的特殊角吗 通 过 课前预习, 学生既可以复习旧知识, 同时了解新知识, 使学生的学习变得更有方向而且有效地突出了本节课的重点, 抓住学生急于探知结论的心理, 为仰角、俯角的概念的引出奠定了良好的基础. 学生猜想,教师引入:以前我们探究了方位角及其应用,今天我们再学习一种新的测量物体高度的角----- 仰角和俯角. 利用教师机的实物 投屏,清晰的展示 学生活动行为,吸 引全体学生注意力, 激发学生的学习兴 趣,有效促进生生 间的互动交流 教师利用教师机让学生在机上描出树叶的边,让学生直观的感知树叶的周长
二. 合作探究, 获取新知 解直角三角形和其它知识一样,在实际问题中有着广泛的应用, 下面我们就来学习一种新的测量物体高度的方法. 师:什么是方位角? 生:是从某点指北方向线起,依顺时针方向到目标方向的线间的夹角叫方位角. 师:想一想,上面的 60° 和 45°是怎样构成的 生:是由视线与水平线 通 过 与方位角的对边, 有利于学生对仰角和俯角概念的理解, 符合学生认识规律. 教师多媒体出示图 2,让学生加深对新知识的感性认识. 利用拍照讲解, 对比对讲,学生看的一目了然, 教师讲解清楚, 学生易懂
组成的角. 师:请同学们归纳下仰角、俯角的概念 生:在进行测量时,由 视线与水平线的夹角中视线在水平线的上方, 视线与水平线的夹角叫仰角,视线在水平线下方,视线与水平线的夹角叫俯角.
三、学以致用, 加深认识 例 1 如图 3 , 学生要测量校园内一颗水杉树的高度,他站在距离水杉树 8m 的 E 处, 测得树顶 的 仰 角 为 ∠ACD=52° , 已知测角器的高度 CE=1.6m , 问树高 AB 为多少米?(精确到 0.1m) 解:在 Rt△ADC 中 ∵∠ACD=50° , CD=BE =8m 又∵tan∠ACD= ∴AD=CD·tan∠ACD =8×tan52° =8×1.2799 ≈10.2(m) ∵DB=CE=1.6m ∴AB=AD+BD=10.2+1.6 通 过 对例题的解答加深了学生对仰角、俯角意义的理解并能熟练加以运用. 想一想:在这个图中, 52° 的仰角指的是哪个角? 议一议:水杉 树的高度可分成几 个部分?如何求解? 学生独立完成 然后同桌交流,代表展示,师生共同纠正. 教师多媒体展 示解题过程,规范 学生的解题步骤. 老师的提问可以设置抢答、随机作答和小组讨论作答 以选择题、判断, 填空题或者主观题等任何形式推送到学生端,这题利用判断的形式学生选 ,择正确的答案,或 者把自己写在纸上的答案拍照上传给老师,老师第一时间看到谁上交了、谁没交,选择题直接出正答率,或者抽取学生有代表性的答案进行点评.
=11.8(m) 答:树高AB 为 11.8m.
四. 探究新知 例 2 如图 4 , 某校九年级学生要测量当地电视塔的高度 AB, 因为不能直接到达塔底 B 处他们采用在发射台院外与电视塔成一直线的C、D 两处的地面上,用测角器测得电视塔顶部A 的仰角分别为 45° 和30° , 同时量得 CD 为 50m, 已知测角器高为 1m,问电视塔的高度为多少米?(精确到 1m). 解:设 AB1=xm. 在 Rt△AC1B1 中, 由 ∠ AC1B1=45° , 得 C1B1=AB1=x 在 Rt△AD1B1 中, 由∠AD1B1=30°,得tan∠AD1B1== 即 3 x 3 50 x 解 方 程 , 得 x=25(+1)≈68 让 学 生经历利用仰角、俯角测量 ,不 可以到达底部的物体高度的探究过程, 增强直角三角形的边角关系在物体高度测量问题中的应用, 进一步提高学生的建模思想及把实际问题转化成数学问题的能力. 想一想:在图中 , 仰 角 45° 和30° 分别指哪两个角? 观察思考:图 中有几个直角三角形?你能得出哪些结论? 议一议:此题 的等量关系是什么电视塔的高度包括几部分? 学生交流讨论 回答问题,然后独立完成后,与同桌交流,代表展示, 师生共同纠正. 利用教师机拍照讲解,对比对讲, 也可利用相机功能让所有学生看的清楚听的明白 ,
∴AB=AB1+B1B≈68+1=6 9(m). 答: 电视塔的高度为 69m.
五.变式训 练 如图 6 , 某直升机于空中 A 处测得正前方地面控制点 C 的俯角为30°;若航向不变,直升机继续向前飞行 1000m 至 B 处,测得地面控制点 C 的俯角为 45°.求直升机再向前飞行多远, 与地面控制点 C 的距离最近(结果保留根号) 设 计 练习是由易到难进行设计的, 目的是除了培养学生一般思维品质的基础外, 还要有意识的培养学生思维的创新。 学生独立完成一名学生演示,其余下面完成,教师巡视,帮助学困生然后集体纠正. 以选择题、判断,填 ,空题或者主观题等 任何形式推送到学 生端,这些题利用 判断的形式,拍照 的形式学生选择正 确的答案,或者把 自己写在纸上的答 案拍照上传给老师, 老师第一时间看到 谁上交了、谁没交, 抽取学生有代表性 的答案进行点评.
六. 思维拓展 如图 5 , 小明在家里楼顶上的点 A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点 A 看电梯楼顶部点 B 处仰角为60°,在点A 处看这栋电梯楼底部点 C 处俯角为45°,两栋楼之间的距离 30m, 求电梯楼 BC 的高 (结果保留根号). 通 过 练习加深对仰角、俯角的理解, 培养学生合作学习的能力, 让学生树立解决问题的信心, 进一步巩固三角函数在解直角三角形中的 应用技巧及 小组合作完成代表展示,教师巡视,帮助学困生, 然后集体纠正. ,
方法, 提高解决问题的综合能力.
七.课 堂 小结 八. 布置作业 通过本节课学习,我们学习了哪些内容? 学生归纳,教师点评: 仰角、俯角概念; 利用仰角、俯角解决实际问题的方法. 【设计意图】通过课堂小结的形式,帮助学生养成整理知识的习惯,加深认识深化提高,形成体系,同时明确学习重点. 教科书 P131 页习题 23.2 第 2,3 题.
