5.5.1第一课时两角差的余弦公式 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共19张ppt)
文档属性
| 名称 | 5.5.1第一课时两角差的余弦公式 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共19张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览




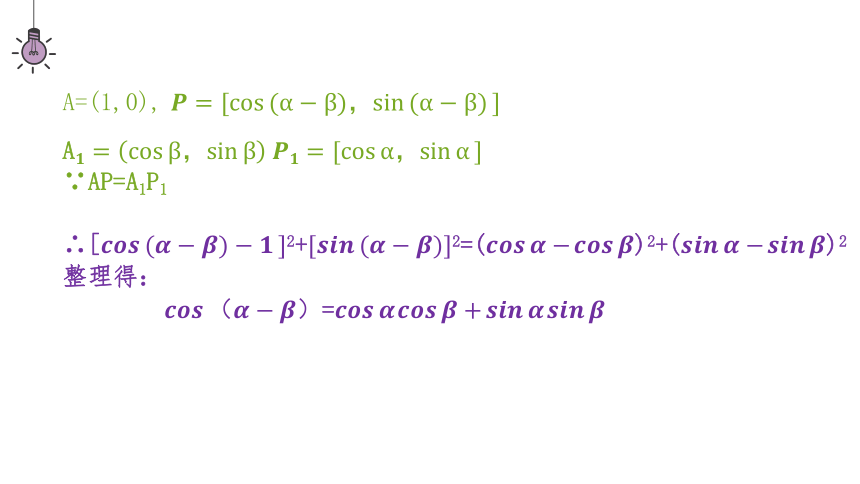
文档简介
(共19张PPT)
5.5.1 两角差的余弦公式
回顾和引入
PART 01
复习回顾
前面我们学习的诱导公式,利用诱导公式可以进行恒等变形。
sin(α+2kπ)=sinα
tan(α+2kπ)=tanα
cos(α+2kπ)=cosα
sin(π+α)=-sinα
tan(π+α)=tanα
cos(π+α)=-cosα
sin(-α)=-sinα
tan(-α)=-tanα
cos(-α)=cosα
sin(π-α)=sinα
tan(π-α)=-tanα
cos(π-α)=-cosα
tan( -α)=cotα
π
2
sin( -α)=cosα
π
2
cos( -α)=sinα
π
2
tan( +α)=-cotα
π
2
sin( +α)=cosα
π
2
cos( +α)=-sinα
π
2
这些都是特殊角与任意角的和或差的三角函数与这个角三角函数的恒等关系
如果把特殊角换为任意角β,那么任意角α与β的和(或差)的三角函数与α,β的三角函数会有什么关系呢?
新课讲授
PART 02
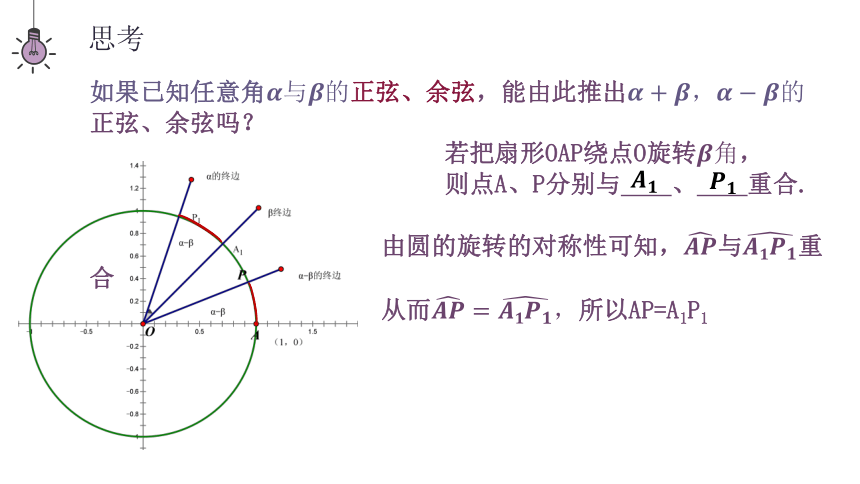
如果已知任意角正弦、余弦,能由此推出
正弦、余弦吗?
若把扇形OAP绕点O旋转,
则点A、P分别与 、 重合.
由圆的旋转的对称性可知,与重合
从而所以AP=A1P1
思考
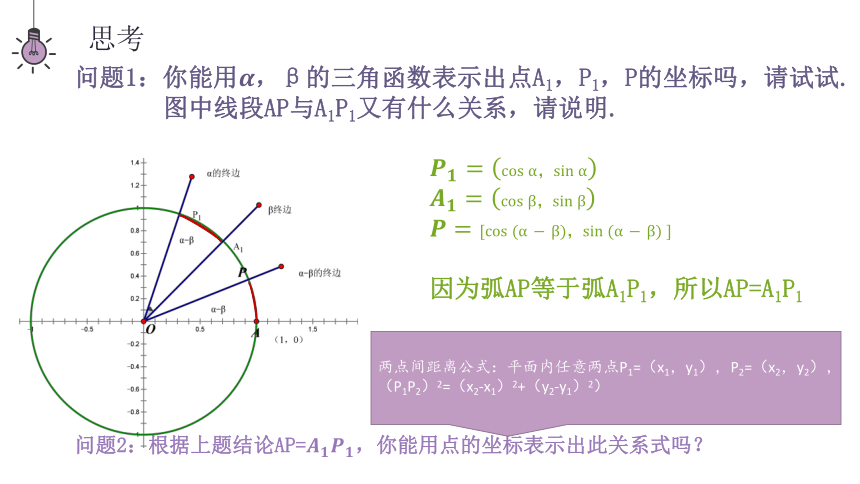
问题1:你能用,β的三角函数表示出点A1,P1,P的坐标吗,请试试.
图中线段AP与A1P1又有什么关系,请说明.
因为弧AP等于弧A1P1,所以AP=A1P1
问题2:根据上题结论AP=,你能用点的坐标表示出此关系式吗?
思考
两点间距离公式:平面内任意两点P1=(x1,y1),P2=(x2,y2),
(P1P2)2=(x2-x1)2+(y2-y1)2)
A=(1,0),
A
∵AP=A1P1
∴[2+2=()2+()2
整理得:
=
=
此公式给出了任意角正弦、余弦与其差角的余弦的关系,称为差角的余弦公式,简记作:C( )
例1.利用差角的余弦公式证明下列诱导公式
解:=
=
例2.已知=,,,,求的值.
总结:由三角函数同角关系式易得,=,
故=
课堂练习
PART 03
1、利用公式C证明:
(1)
(2)
利用差角余弦公式证明
证明:(1)
(2)
2、利用公式C求cos15°的值.
解:cos15°=cos(45°-30°)
=cos45°cos30°+sin45°sin30°
=
=
利用差角余弦公式求值
3、已知值.
解: ∵sin2=1-cos2,
∴ sin2=
∵
∴ sin=
∵ =
=
=
利用差角余弦公式求值
点拨:①利用sin2=1-cos2-1可求sin.
②利用差角余弦公式求值.
4、已知第二象限角,求
利用差角余弦公式求值
解: ∵cos2=1-sin2,
∴ cos2=
∵
∴ =
∵ =
=
=
5.已知
利用差角余弦公式求值
解: ∵cos2=1-sin2,
∴ cos2=
∵
∴ =
同理:
∴ =
=
=
小结
PART 04
小结
=
谢谢
5.5.1 两角差的余弦公式
回顾和引入
PART 01
复习回顾
前面我们学习的诱导公式,利用诱导公式可以进行恒等变形。
sin(α+2kπ)=sinα
tan(α+2kπ)=tanα
cos(α+2kπ)=cosα
sin(π+α)=-sinα
tan(π+α)=tanα
cos(π+α)=-cosα
sin(-α)=-sinα
tan(-α)=-tanα
cos(-α)=cosα
sin(π-α)=sinα
tan(π-α)=-tanα
cos(π-α)=-cosα
tan( -α)=cotα
π
2
sin( -α)=cosα
π
2
cos( -α)=sinα
π
2
tan( +α)=-cotα
π
2
sin( +α)=cosα
π
2
cos( +α)=-sinα
π
2
这些都是特殊角与任意角的和或差的三角函数与这个角三角函数的恒等关系
如果把特殊角换为任意角β,那么任意角α与β的和(或差)的三角函数与α,β的三角函数会有什么关系呢?
新课讲授
PART 02
如果已知任意角正弦、余弦,能由此推出
正弦、余弦吗?
若把扇形OAP绕点O旋转,
则点A、P分别与 、 重合.
由圆的旋转的对称性可知,与重合
从而所以AP=A1P1
思考
问题1:你能用,β的三角函数表示出点A1,P1,P的坐标吗,请试试.
图中线段AP与A1P1又有什么关系,请说明.
因为弧AP等于弧A1P1,所以AP=A1P1
问题2:根据上题结论AP=,你能用点的坐标表示出此关系式吗?
思考
两点间距离公式:平面内任意两点P1=(x1,y1),P2=(x2,y2),
(P1P2)2=(x2-x1)2+(y2-y1)2)
A=(1,0),
A
∵AP=A1P1
∴[2+2=()2+()2
整理得:
=
=
此公式给出了任意角正弦、余弦与其差角的余弦的关系,称为差角的余弦公式,简记作:C( )
例1.利用差角的余弦公式证明下列诱导公式
解:=
=
例2.已知=,,,,求的值.
总结:由三角函数同角关系式易得,=,
故=
课堂练习
PART 03
1、利用公式C证明:
(1)
(2)
利用差角余弦公式证明
证明:(1)
(2)
2、利用公式C求cos15°的值.
解:cos15°=cos(45°-30°)
=cos45°cos30°+sin45°sin30°
=
=
利用差角余弦公式求值
3、已知值.
解: ∵sin2=1-cos2,
∴ sin2=
∵
∴ sin=
∵ =
=
=
利用差角余弦公式求值
点拨:①利用sin2=1-cos2-1可求sin.
②利用差角余弦公式求值.
4、已知第二象限角,求
利用差角余弦公式求值
解: ∵cos2=1-sin2,
∴ cos2=
∵
∴ =
∵ =
=
=
5.已知
利用差角余弦公式求值
解: ∵cos2=1-sin2,
∴ cos2=
∵
∴ =
同理:
∴ =
=
=
小结
PART 04
小结
=
谢谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
