2021-2022学年北师大版八年级数学下册第一章三角形的证明单元测试卷(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册第一章三角形的证明单元测试卷(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 122.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 22:05:41 | ||
图片预览


文档简介
第一章三角形的证明单元测试卷 2021-2022学年北师大版八年级数学下册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A. B.
C. D.
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C,D为圆心,大于的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是 ( )
A. 射线是的平分线
B. 是等腰三角形
C. ,两点关于所在直线对称
D. ,两点关于所在直线对称
如图,A,B,C三个居民小区的位置构成三角形,现决定在三个小区之间修建一个超市,使超市到三个小区的距离相等,则超市应建在( )
A. ,两边高的交点处
B. ,两边中线的交点处
C. ,两边垂直平分线的交点处
D. ,两内角平分线的交点处
如图,在中,,线段AB的垂直平分线交AC于点N,的周长是7 cm,则BC的长为( )
A. B.
C. D.
如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A. B.
C. D.
如图,已知点P是ABC的内角平分线的交点,BPC=,则A的度数是( )
A. B.
C. D.
如图,在ABC中,AB=AC,AD=DE,BAD=,EDC=,则DAE的度数为( )
A. B.
C. D.
如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A. B. C. D.
等腰三角形一腰上的高等于腰长的一半,则顶角的度数是( )
A. B. C. 或 D. 不能确定
如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线BM为ABC的平分线,l与BM相交于P点.若A=,ACP=,则ABP的度数为( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
用反证法证明“三角形的内角中最多有一个角是直角”时应假设:______.
等腰三角形的周长为16,其一边长为6,则另两边的长为______ .
如图,O为ABC三边垂直平分线的交点,若OAB=,OBC=,则OCA= .
如图,已知在△ ABC中,AB=BC,∠ B=120°,AB的垂直平分线交AC于点D.若AC=6 cm,则AD=__________ cm.
如图,在RtABC中,A=,BD平分ABC交AC于点D,=4,BC=8,则AD= .
三、解答题(本大题共5小题,共55分)
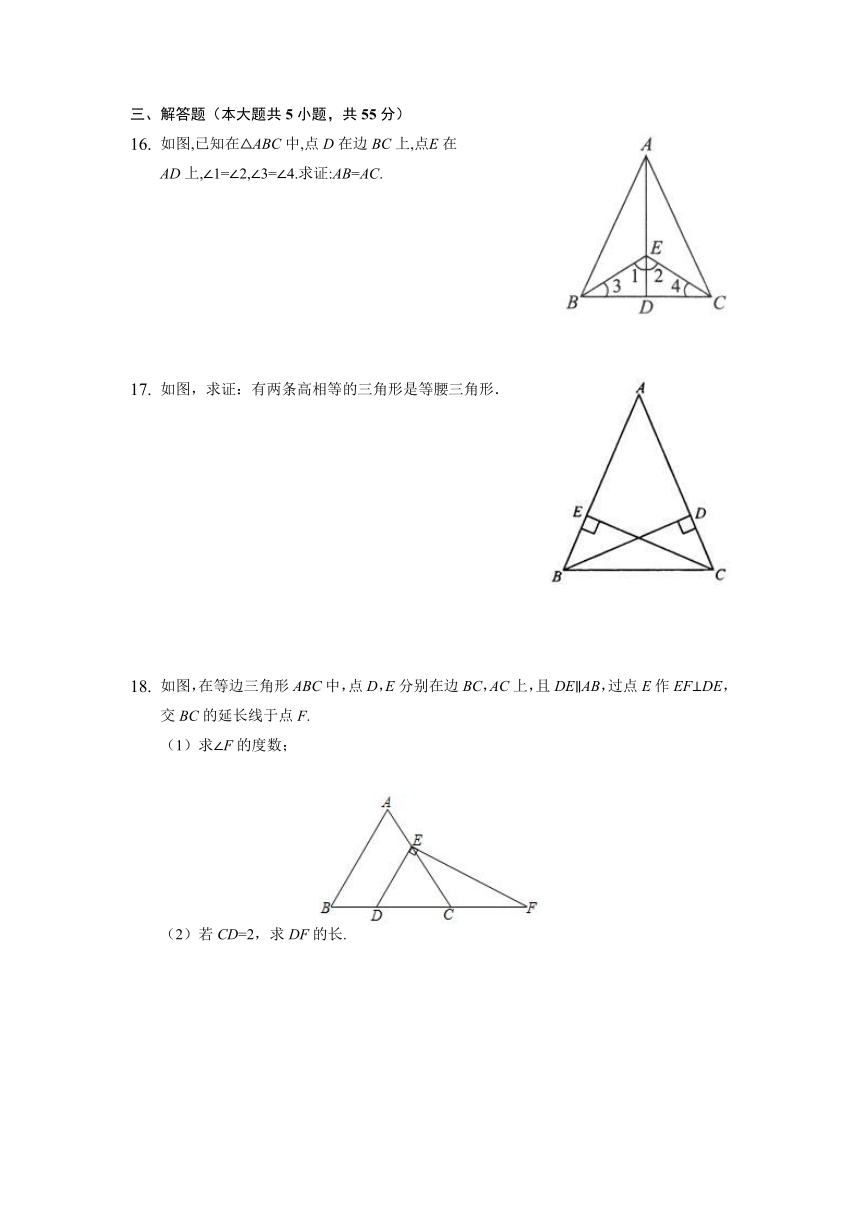
如图,已知在ABC中,点D在边BC上,点E在AD上,1=2,3=4.求证:AB=AC.
如图,求证:有两条高相等的三角形是等腰三角形.
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
如图,AB=AC,ADBC,CEAB,垂足分别为D,E,AE=CE.求证:
(1)AEFCEB;
(2)AF=2CD.
如图,在RtABC中,BAC=,AC=2AB,点D是AC的中点,将一块锐角为的三角尺如图放置,三角尺斜边的两个端点巧好分别与A,D重合,连接BE,CE,试猜想线段BE和CE的数量及位置关系,并证明你的猜想.
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】三角形中至少有两个角是直角
12.【答案】6,4或5,5
13.【答案】40°
14.【答案】2
15.【答案】1
16.【答案】证明:3=4,
BE=CE.
1=2,
BD=CD,ADBC,
AB=AC.
17.【答案】已知:在△ABC中,BD⊥AC于点D,CE⊥AB于点E,且BD=CE,
求证:△ABC是等腰三角形.(或AB=AC)
证明:∵BD⊥AC于点D,CE⊥AB于点E,
∴∠BDC=∠CEB=90°,
在△BDC和△CEB中,
∵BD=CE,BC=CB,
∴△BDC≌△CEB(HL),
∴∠DCB=∠EBC,
∴AB=AC,
即△ABC是等腰三角形.
18.【答案】解:(1)∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE∥AB,
∴∠B=EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°,
∵EF⊥ED,
∴∠DEF=90°,
∴∠F=30°;
(2)∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,
∴CE=CF.
∵∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2.
∴CF=2.
∴DF=DC+CF=2+2=4.
19.【答案】证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
20.【答案】解:数量关系为:BE=EC,位置关系是:BE⊥EC.
证明:∵△AED是直角三角形,∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC-∠EDA=180°-45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=AC,
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中
,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°,
∴BE⊥EC.
第4页,共8页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A. B.
C. D.
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C,D为圆心,大于的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是 ( )
A. 射线是的平分线
B. 是等腰三角形
C. ,两点关于所在直线对称
D. ,两点关于所在直线对称
如图,A,B,C三个居民小区的位置构成三角形,现决定在三个小区之间修建一个超市,使超市到三个小区的距离相等,则超市应建在( )
A. ,两边高的交点处
B. ,两边中线的交点处
C. ,两边垂直平分线的交点处
D. ,两内角平分线的交点处
如图,在中,,线段AB的垂直平分线交AC于点N,的周长是7 cm,则BC的长为( )
A. B.
C. D.
如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A. B.
C. D.
如图,已知点P是ABC的内角平分线的交点,BPC=,则A的度数是( )
A. B.
C. D.
如图,在ABC中,AB=AC,AD=DE,BAD=,EDC=,则DAE的度数为( )
A. B.
C. D.
如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A. B. C. D.
等腰三角形一腰上的高等于腰长的一半,则顶角的度数是( )
A. B. C. 或 D. 不能确定
如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线BM为ABC的平分线,l与BM相交于P点.若A=,ACP=,则ABP的度数为( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
用反证法证明“三角形的内角中最多有一个角是直角”时应假设:______.
等腰三角形的周长为16,其一边长为6,则另两边的长为______ .
如图,O为ABC三边垂直平分线的交点,若OAB=,OBC=,则OCA= .
如图,已知在△ ABC中,AB=BC,∠ B=120°,AB的垂直平分线交AC于点D.若AC=6 cm,则AD=__________ cm.
如图,在RtABC中,A=,BD平分ABC交AC于点D,=4,BC=8,则AD= .
三、解答题(本大题共5小题,共55分)
如图,已知在ABC中,点D在边BC上,点E在AD上,1=2,3=4.求证:AB=AC.
如图,求证:有两条高相等的三角形是等腰三角形.
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
如图,AB=AC,ADBC,CEAB,垂足分别为D,E,AE=CE.求证:
(1)AEFCEB;
(2)AF=2CD.
如图,在RtABC中,BAC=,AC=2AB,点D是AC的中点,将一块锐角为的三角尺如图放置,三角尺斜边的两个端点巧好分别与A,D重合,连接BE,CE,试猜想线段BE和CE的数量及位置关系,并证明你的猜想.
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】三角形中至少有两个角是直角
12.【答案】6,4或5,5
13.【答案】40°
14.【答案】2
15.【答案】1
16.【答案】证明:3=4,
BE=CE.
1=2,
BD=CD,ADBC,
AB=AC.
17.【答案】已知:在△ABC中,BD⊥AC于点D,CE⊥AB于点E,且BD=CE,
求证:△ABC是等腰三角形.(或AB=AC)
证明:∵BD⊥AC于点D,CE⊥AB于点E,
∴∠BDC=∠CEB=90°,
在△BDC和△CEB中,
∵BD=CE,BC=CB,
∴△BDC≌△CEB(HL),
∴∠DCB=∠EBC,
∴AB=AC,
即△ABC是等腰三角形.
18.【答案】解:(1)∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE∥AB,
∴∠B=EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°,
∵EF⊥ED,
∴∠DEF=90°,
∴∠F=30°;
(2)∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,
∴CE=CF.
∵∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2.
∴CF=2.
∴DF=DC+CF=2+2=4.
19.【答案】证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
20.【答案】解:数量关系为:BE=EC,位置关系是:BE⊥EC.
证明:∵△AED是直角三角形,∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC-∠EDA=180°-45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=AC,
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中
,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°,
∴BE⊥EC.
第4页,共8页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
