2021-2022学年高二上学期数学 人教A版(2019)选择性必修第二册4.1 数列的概念 (第二课时)课件(共19张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学 人教A版(2019)选择性必修第二册4.1 数列的概念 (第二课时)课件(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 817.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第四章 数列
4.1 数列的概念(第二课时)
数列的通项公式与递推公式
了解递推公式是给出数列的一种方式.
01
理解递推公式的含义,能够根据递推公式写出数列的前几项.
02
掌握由一些简单的递推公式求数列的通项公式的方法和研究数列的单调性的方法.
03
培养逻辑推理、数学抽象的学科素养.
04
素养目标
情境引入
例3 如果数列的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
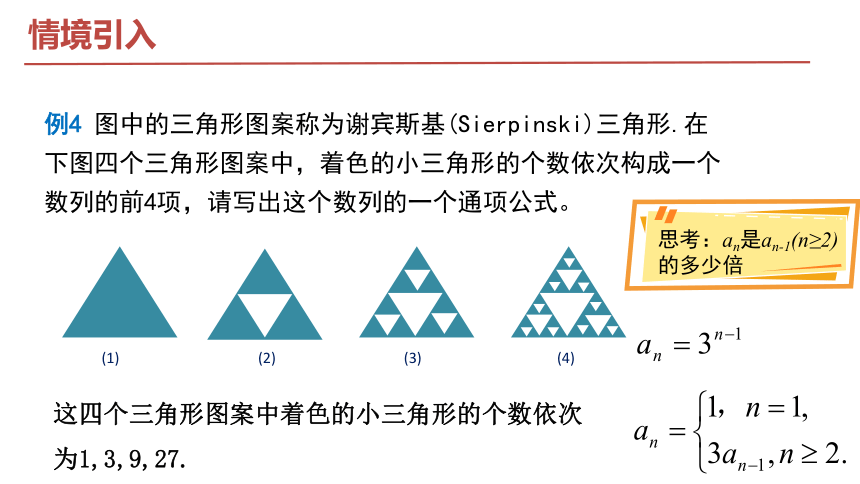
例4 图中的三角形图案称为谢宾斯基(Sierpinski)三角形.在下图四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式。
(1)
(2)
(3)
(4)
这四个三角形图案中着色的小三角形的个数依次为1,3,9,27.
情境引入
思考:an是an-1(n≥2)的多少倍
像 这样,如果一个数列的相邻两项或多项之间可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项和递推公式,就能求出数列的每一项了
新知探究
一、递推公式定义:
新知探究
二、 由递推公式写出数列的项
新知探究
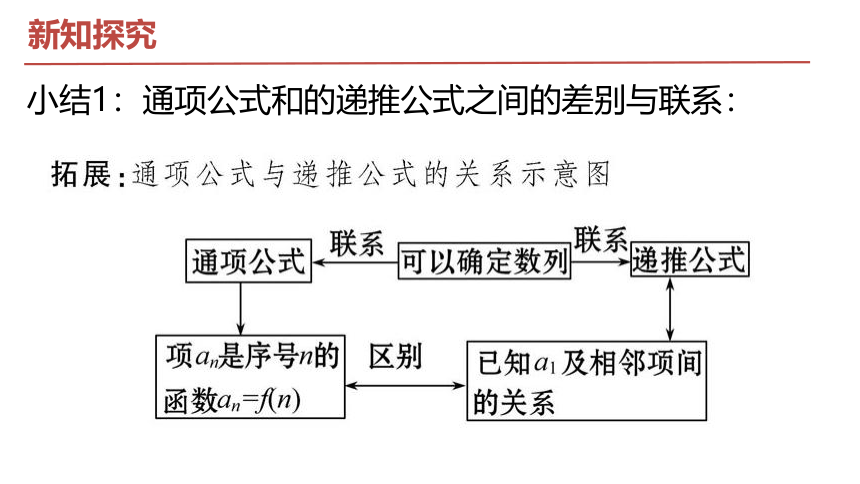
小结1:通项公式和的递推公式之间的差别与联系:
新知探究
小结2:由递推公式写出数列的项的方法
根据递推公式写出数列的前几项,首先要弄清楚公式中各部分的关系,依次代入计算即可.
01
若知道的是首项,通常将所给公式整理成用前面的项表示后面的项的形式.
02
若知道的是末项,通常将所给公式整理成用后面的项表示前面的项的形式.
03
练习巩固
练习巩固
(2)在数列{an}中,a1=1,an=an-1+
1
n(n-1)
(n≥2).
练习2:已知下列数列的递推公式,写出此数列的前 4 项,
并推测数列的通项公式.
(1)数列{an}满足 an+1=2an+1,n∈N*,且 a1=-1;
(3)a1=0,an+1=an+(2n-1)(n∈N*);
(4)a1=1,an+1=
2an
an+2
(n∈N*).
新知探究
例2:已知在数列{an}中,a1=5,an=an-1+3(n≥2),求数
列{an}的通项公式.
总结归纳:若数列有形如an+1=an+f(n)的递推公式,且可
求 f(1)+f(2)+…+f(n),可用累加法求通项公式.
二、 已知数列的递推公式,用累加法求通项公式
新知探究
例3:已知a1=2,an+1=2an,求an.
三、 已知数列的递推公式,用累乘法求通项公式
练习巩固
练习巩固
练习巩固
练习巩固
新知探究
四、 数列的前n项和
新知探究
课堂小结
第四章 数列
4.1 数列的概念(第二课时)
数列的通项公式与递推公式
了解递推公式是给出数列的一种方式.
01
理解递推公式的含义,能够根据递推公式写出数列的前几项.
02
掌握由一些简单的递推公式求数列的通项公式的方法和研究数列的单调性的方法.
03
培养逻辑推理、数学抽象的学科素养.
04
素养目标
情境引入
例3 如果数列的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
例4 图中的三角形图案称为谢宾斯基(Sierpinski)三角形.在下图四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式。
(1)
(2)
(3)
(4)
这四个三角形图案中着色的小三角形的个数依次为1,3,9,27.
情境引入
思考:an是an-1(n≥2)的多少倍
像 这样,如果一个数列的相邻两项或多项之间可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项和递推公式,就能求出数列的每一项了
新知探究
一、递推公式定义:
新知探究
二、 由递推公式写出数列的项
新知探究
小结1:通项公式和的递推公式之间的差别与联系:
新知探究
小结2:由递推公式写出数列的项的方法
根据递推公式写出数列的前几项,首先要弄清楚公式中各部分的关系,依次代入计算即可.
01
若知道的是首项,通常将所给公式整理成用前面的项表示后面的项的形式.
02
若知道的是末项,通常将所给公式整理成用后面的项表示前面的项的形式.
03
练习巩固
练习巩固
(2)在数列{an}中,a1=1,an=an-1+
1
n(n-1)
(n≥2).
练习2:已知下列数列的递推公式,写出此数列的前 4 项,
并推测数列的通项公式.
(1)数列{an}满足 an+1=2an+1,n∈N*,且 a1=-1;
(3)a1=0,an+1=an+(2n-1)(n∈N*);
(4)a1=1,an+1=
2an
an+2
(n∈N*).
新知探究
例2:已知在数列{an}中,a1=5,an=an-1+3(n≥2),求数
列{an}的通项公式.
总结归纳:若数列有形如an+1=an+f(n)的递推公式,且可
求 f(1)+f(2)+…+f(n),可用累加法求通项公式.
二、 已知数列的递推公式,用累加法求通项公式
新知探究
例3:已知a1=2,an+1=2an,求an.
三、 已知数列的递推公式,用累乘法求通项公式
练习巩固
练习巩固
练习巩固
练习巩固
新知探究
四、 数列的前n项和
新知探究
课堂小结
