5.3.1 第2课时 平行线的性质和判定及其综合运用 课件(共29张PPT)
文档属性
| 名称 | 5.3.1 第2课时 平行线的性质和判定及其综合运用 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 21:35:37 | ||
图片预览





文档简介
(共29张PPT)
平行线的性质和判定及其综合运用
人教版数学 七年级下册
学习目标
01
学习目标
知道两直线平行的断定方法,了解平行线的性质。
理解平行线的性质与判定方法,运用平行线的性质与判定解决一些问题。
新课教学
02
性质1 两条平行线被第三条直线所截,同位角相等。
性质2 两条平行线被第三条直线所截,内错角相等。
性质3 两条平行线被第三条直线所截,同旁内角互补。
问题1 平行线的三条性质分别是什么?
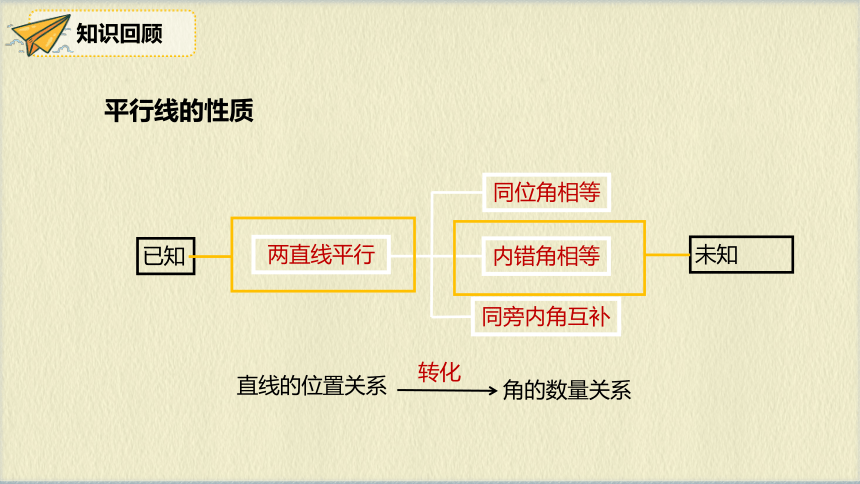
知识回顾
学行线的性质后,我们能解决什么问题?
同旁内角互补
同位角相等
内错角相等
两直线平行
平行线的性质
未知
已知
直线的位置关系
角的数量关系
转化
知识回顾
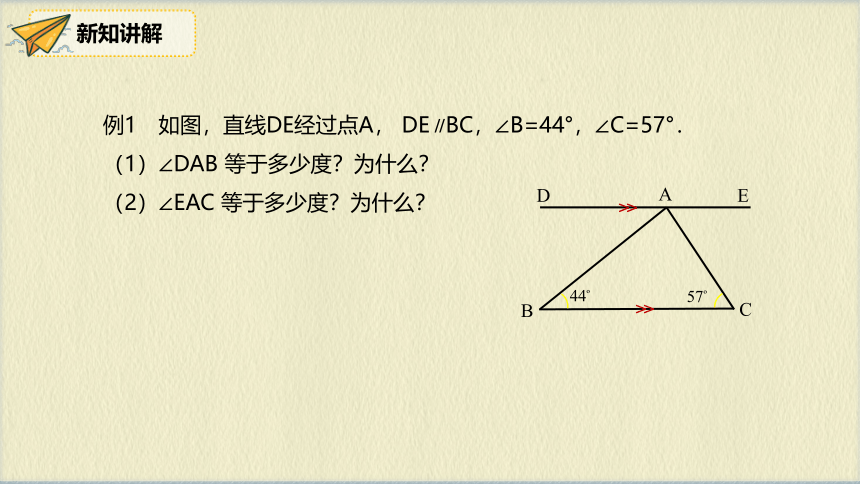
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
(2)∠EAC 等于多少度?为什么?
A
D
E
B
C
44
57
新知讲解
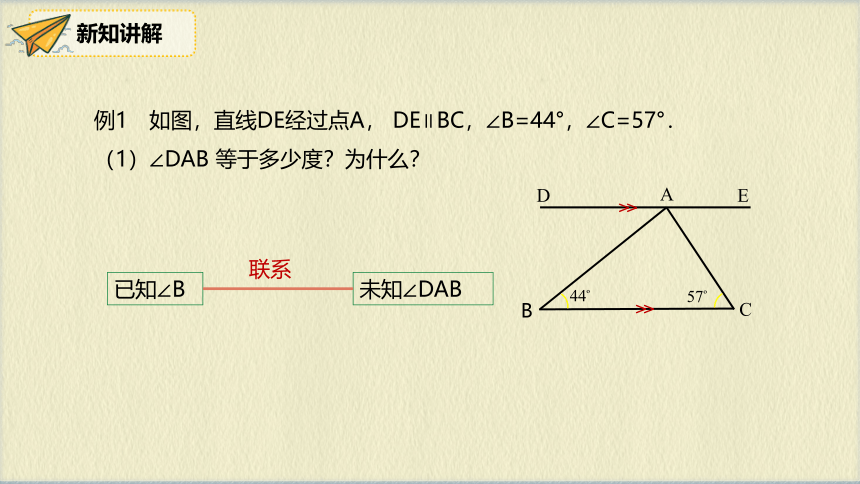
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
已知∠B
未知∠DAB
联系
新知讲解
A
D
E
B
C
44
57
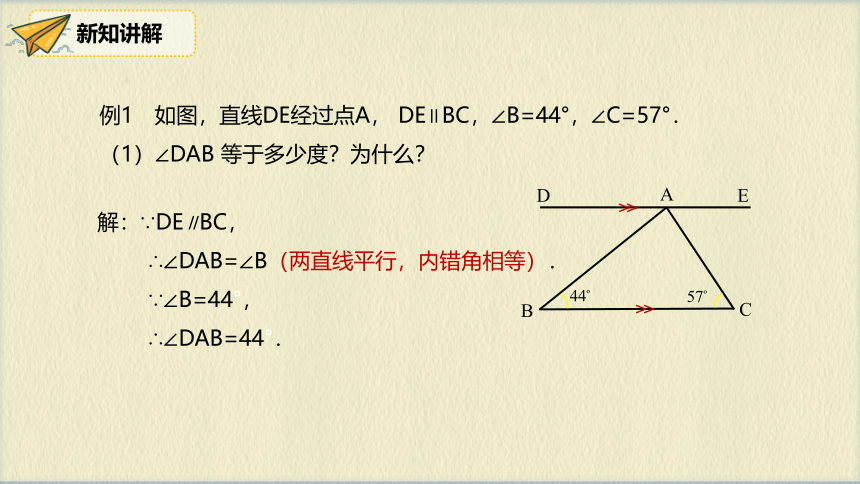
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
解:∵DE∥BC,
∴∠DAB=∠B(两直线平行,内错角相等).
∵∠B=44°,
∴∠DAB=44°.
新知讲解
A
D
E
B
C
44
57
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(2)∠EAC 等于多少度?为什么?
已知
未知
联系
解:∵DE∥BC,
∴∠EAC=∠C(两直线平行,内错角相等)
∵∠C=57°,
∴∠EAC=57°.
A
D
E
C
44
57
新知讲解
A
B
C
D
E
60
60
40
?
A
B
C
D
E
两个角是同位角
这两个角相等
×
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
新知讲解
A
B
C
D
E
60
60
40
?
∠C的度数
∠ADE=60°,∠B=60°
DE∥BC
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
新知讲解
解:∵∠ADE=60°,∠B=60°(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠C=∠AED(两直线平行,同位角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
A
B
C
D
E
60
60
40
?
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
新知讲解
点D,E分别在线段AB,AC上
点D,E分别在线段AB ,AC的延长线上
点D,E分别在线段BA,CA的延长线上
三种情况
已研究
问题2 如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立吗?
A
B
C
新知讲解
点D,E分别在线段AB,AC上
60
60
E
A
B
C
D
∠ADE与∠ABC相等的同位角
DE∥BC
40
∠ACB=∠AED=40°
?
点D,E分别在线段AB ,AC的延长线上
新知讲解
解:∵ ∠ADE=60°,∠B=60°(已知),
∴ ∠ADE=∠B(等量代换).
∴ DE∥BC(内错角相等,两直线平行).
∴∠C=∠AED(两直线平行,内错角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
A
B
C
D
E
60
60
40
?
点D,E分别在线段BA ,CA的延长线上
新知讲解
同位角
同位角
内错角
A
B
C
D
E
图1
A
B
C
D
E
图2
图3
A
B
C
D
E
如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立.
新知讲解
小试牛刀
03
1.如图,在梯形ABCD中,∠A=100°,∠B=115°,求∠C与∠D的度数.
小试牛刀
解:因为梯形上、下两底AB与CD互相平行,
根据“两直线平行,同旁内角互补”,
可得∠A与∠D互补,∠B与∠C互补.
于是
∠D=180 -∠A=180°-100°=80°,
∠C=180 -∠B=180°-115°=65°.
所以梯形的另外两个角分别为80°,65°.
C
D
100
115
B
A
4
1
2
3
5
6
B
A
C
D
E
F
G
H
证明:∵ EF∥GH,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4.
∵∠5=180°-∠1-∠2,∠6=180°-∠3-∠4,
∴∠5=∠6.
∴AB∥CD(内错角相等,两直线平行).
2.如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
小试牛刀
3.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD 的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
小试牛刀
4.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,第二次的拐角∠B是多少度?为什么?
A
B
小试牛刀
5.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
8
7
6
5
4
3
2
1
水
空气
小试牛刀
延伸拓展
04
如图, AB∥CD,GH分别交AB和CD于点E和点M ,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
猜想EF∥MN
例3 两条平行线被第三条直线所截,形成的任意一组同位角的角平分线
具有怎样的位置关系?
A
G
H
C
M
D
B
N
E
F
F
F
E
M
N
延伸拓展
课堂小结
05
已知、未知是什么?条件是什么?
能否借助条件让已知与未知产生联系
以前是否解决过类似问题?能否类比进行求解?
在解决问题时,我们可以这样进行思考:
已知
未知
联系
想可知
想需知
课堂小结
课堂小结
这个问题的解决思路是什么?能用这种思路解决什么类型的问题?
在解决这个问题时,关键在哪里?自己是如何突破的?
改变问题中的部分条件,结果还成立吗?
得到的结论具有一般性吗?
在解决问题后,我们可以进行这样的反思:
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
平行线的性质和判定及其综合运用
人教版数学 七年级下册
学习目标
01
学习目标
知道两直线平行的断定方法,了解平行线的性质。
理解平行线的性质与判定方法,运用平行线的性质与判定解决一些问题。
新课教学
02
性质1 两条平行线被第三条直线所截,同位角相等。
性质2 两条平行线被第三条直线所截,内错角相等。
性质3 两条平行线被第三条直线所截,同旁内角互补。
问题1 平行线的三条性质分别是什么?
知识回顾
学行线的性质后,我们能解决什么问题?
同旁内角互补
同位角相等
内错角相等
两直线平行
平行线的性质
未知
已知
直线的位置关系
角的数量关系
转化
知识回顾
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
(2)∠EAC 等于多少度?为什么?
A
D
E
B
C
44
57
新知讲解
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
已知∠B
未知∠DAB
联系
新知讲解
A
D
E
B
C
44
57
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
解:∵DE∥BC,
∴∠DAB=∠B(两直线平行,内错角相等).
∵∠B=44°,
∴∠DAB=44°.
新知讲解
A
D
E
B
C
44
57
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(2)∠EAC 等于多少度?为什么?
已知
未知
联系
解:∵DE∥BC,
∴∠EAC=∠C(两直线平行,内错角相等)
∵∠C=57°,
∴∠EAC=57°.
A
D
E
C
44
57
新知讲解
A
B
C
D
E
60
60
40
?
A
B
C
D
E
两个角是同位角
这两个角相等
×
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
新知讲解
A
B
C
D
E
60
60
40
?
∠C的度数
∠ADE=60°,∠B=60°
DE∥BC
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
新知讲解
解:∵∠ADE=60°,∠B=60°(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠C=∠AED(两直线平行,同位角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
A
B
C
D
E
60
60
40
?
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
新知讲解
点D,E分别在线段AB,AC上
点D,E分别在线段AB ,AC的延长线上
点D,E分别在线段BA,CA的延长线上
三种情况
已研究
问题2 如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立吗?
A
B
C
新知讲解
点D,E分别在线段AB,AC上
60
60
E
A
B
C
D
∠ADE与∠ABC相等的同位角
DE∥BC
40
∠ACB=∠AED=40°
?
点D,E分别在线段AB ,AC的延长线上
新知讲解
解:∵ ∠ADE=60°,∠B=60°(已知),
∴ ∠ADE=∠B(等量代换).
∴ DE∥BC(内错角相等,两直线平行).
∴∠C=∠AED(两直线平行,内错角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
A
B
C
D
E
60
60
40
?
点D,E分别在线段BA ,CA的延长线上
新知讲解
同位角
同位角
内错角
A
B
C
D
E
图1
A
B
C
D
E
图2
图3
A
B
C
D
E
如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立.
新知讲解
小试牛刀
03
1.如图,在梯形ABCD中,∠A=100°,∠B=115°,求∠C与∠D的度数.
小试牛刀
解:因为梯形上、下两底AB与CD互相平行,
根据“两直线平行,同旁内角互补”,
可得∠A与∠D互补,∠B与∠C互补.
于是
∠D=180 -∠A=180°-100°=80°,
∠C=180 -∠B=180°-115°=65°.
所以梯形的另外两个角分别为80°,65°.
C
D
100
115
B
A
4
1
2
3
5
6
B
A
C
D
E
F
G
H
证明:∵ EF∥GH,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4.
∵∠5=180°-∠1-∠2,∠6=180°-∠3-∠4,
∴∠5=∠6.
∴AB∥CD(内错角相等,两直线平行).
2.如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
小试牛刀
3.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD 的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
小试牛刀
4.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,第二次的拐角∠B是多少度?为什么?
A
B
小试牛刀
5.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
8
7
6
5
4
3
2
1
水
空气
小试牛刀
延伸拓展
04
如图, AB∥CD,GH分别交AB和CD于点E和点M ,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
猜想EF∥MN
例3 两条平行线被第三条直线所截,形成的任意一组同位角的角平分线
具有怎样的位置关系?
A
G
H
C
M
D
B
N
E
F
F
F
E
M
N
延伸拓展
课堂小结
05
已知、未知是什么?条件是什么?
能否借助条件让已知与未知产生联系
以前是否解决过类似问题?能否类比进行求解?
在解决问题时,我们可以这样进行思考:
已知
未知
联系
想可知
想需知
课堂小结
课堂小结
这个问题的解决思路是什么?能用这种思路解决什么类型的问题?
在解决这个问题时,关键在哪里?自己是如何突破的?
改变问题中的部分条件,结果还成立吗?
得到的结论具有一般性吗?
在解决问题后,我们可以进行这样的反思:
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
