鲁教版(五四制)数学七年级上册 4.2 平方根-第一课时_课件(共21张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 4.2 平方根-第一课时_课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 568.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第一课时
平方根
Contents
目录
01
02
03
04
新知探究
牛刀小试
课堂小结
应用举例
情境导入
05
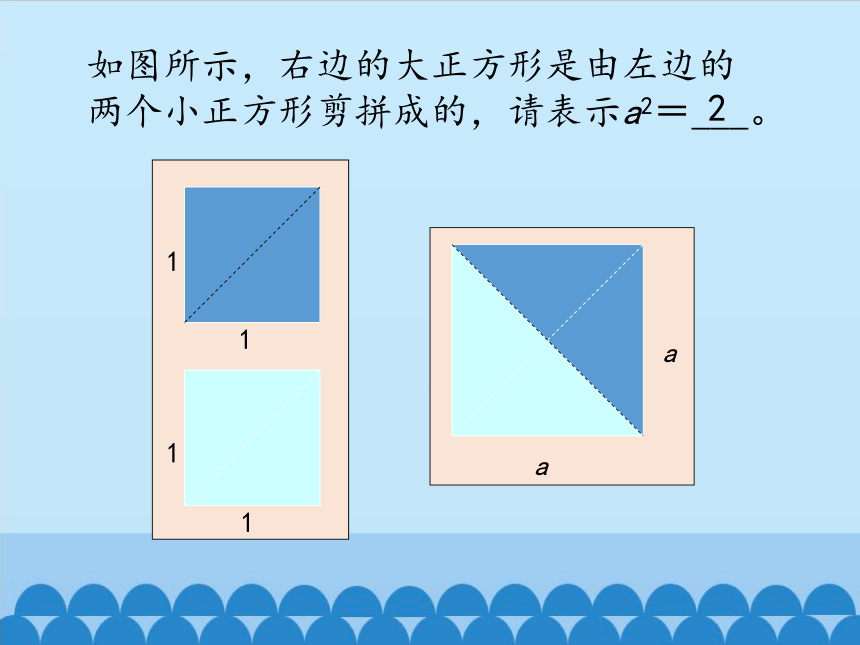
1
1
1
1
a
a
如图所示,右边的大正方形是由左边的两个小正方形剪拼成的,请表示a2=___。
2
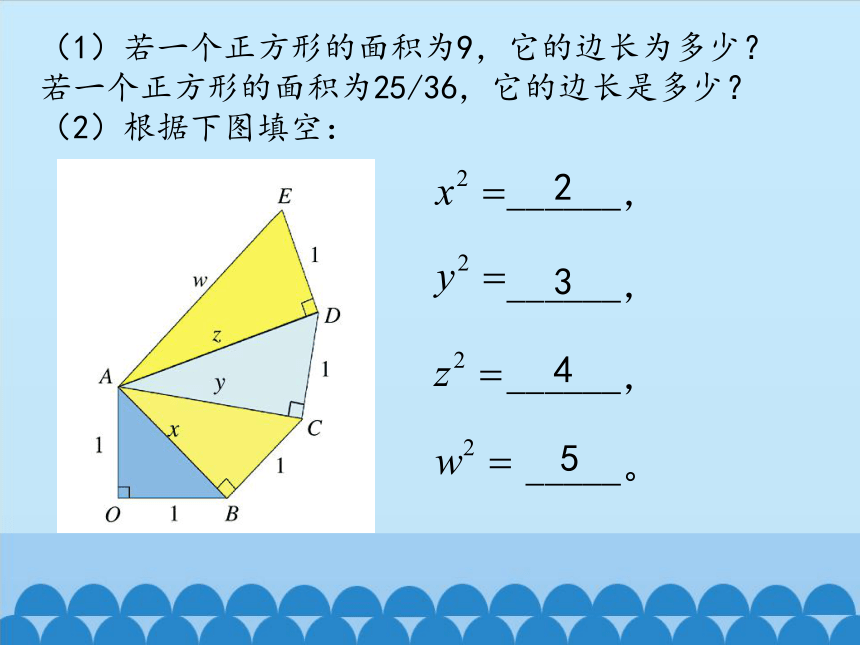
(1)若一个正方形的面积为9,它的边长为多少?若一个正方形的面积为25/36,它的边长是多少?
(2)根据下图填空:
______,
______,
______,
_____。
2
3
4
5
x,y,z,w四个数中哪些是有理数?哪些是无理数?你能表示它们吗?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根,记为“ ”,读作“根号a”。
特别地,我们规定0的算术平方根是0,即 。
注意!
解:(1)因为302=900,所以900的算术平方根是30,即 ;
(2)因为12=1,所以1的算术平方根是1,即 ;
例1:求下列各数的算术平方根:
(1)900;(2)1;(3) ;(4)14。
解:(3)因为 ,所以 的算术平方根是 ,即 ;
例1:求下列各数的算术平方根:
(1)900;(2)1;(3) ;(4)14。
(4)14的算术平方根是 。
注意!
非平方数的算术平方根只能用根号表示。
例2:自由下落物体的高度s(m)与下落时间t(s)的关系为 。有一铁球从19.6m高的建筑物上自由下落,到达地面需要多长时间?
解:将s=19.6代入公式
,
得 ,
所以正数 (s)。
即铁球到达地面需要2s。
注意!
式子 的两层含义:
(1)a≥0;
(2) ≥0。
如果将一个长方形ABCD折叠,得到一个面积为144cm2的正方形ABFE,已知正方形ABFE的面积等于长方形CDEF面积的2倍,求长方形ABCD的长和宽。
A
B
C
D
E
F
知识拓展例题
解:设正方形ABFE的边长为a,
有 ,所以 ,
所以 。
又因为 ,设 ,
所以 , 。
所以 (cm)。
所以长方形的长为18cm,宽为
12cm。
A
B
C
D
E
F
一、填空题:1.若一个数的算术平方根是 ,那么这个数是______;
2. 的算术平方根是______;
3. 的算术平方根是______;
4.若 ,则 ____。
7
16
二、求下列各数的算术平方根:
36, ,15,0.64, , , 。
(2)因为 ,所以 的算术平方根是 ,即 ;
解:(1)因为 ,所以36的算术平方
根是6,即 ;
(3)15的算术平方根是 ;
解:(4)因为0.82=0.64,所以0.64的算术平
方根是0.8,即 ;
(5)因为 ,所以10-4的算术平方根是10-2,即 ;
(6)因为 ,所以 的算术平方根是 ;
(7)因为 ,所以 的算术平方根是1。
36, ,15,0.64, , , 。
三、如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷。若绳子的长度为5.5m,地面固定点C到帐篷支撑竿底部B的距离是4.5m,则帐篷支撑竿的高是多少?(精确到0.1m)
解:由题意得AC=5.5米,BC=4。5米,∠ABC=90°,在Rt△ ABC中,由勾股定理得:
所以帐篷支撑竿的高是3.2m。
(1)算术平方根的概念,式子 中的双重非负性:
一是a≥0,
二是 ≥0。
(2)算术平方根的性质:
一个正数的算术平方根是一个正数;
0的算术平方根是0;负数没有算术平方根。
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根。
习题4.3
作业布置
谢 谢
第一课时
平方根
Contents
目录
01
02
03
04
新知探究
牛刀小试
课堂小结
应用举例
情境导入
05
1
1
1
1
a
a
如图所示,右边的大正方形是由左边的两个小正方形剪拼成的,请表示a2=___。
2
(1)若一个正方形的面积为9,它的边长为多少?若一个正方形的面积为25/36,它的边长是多少?
(2)根据下图填空:
______,
______,
______,
_____。
2
3
4
5
x,y,z,w四个数中哪些是有理数?哪些是无理数?你能表示它们吗?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根,记为“ ”,读作“根号a”。
特别地,我们规定0的算术平方根是0,即 。
注意!
解:(1)因为302=900,所以900的算术平方根是30,即 ;
(2)因为12=1,所以1的算术平方根是1,即 ;
例1:求下列各数的算术平方根:
(1)900;(2)1;(3) ;(4)14。
解:(3)因为 ,所以 的算术平方根是 ,即 ;
例1:求下列各数的算术平方根:
(1)900;(2)1;(3) ;(4)14。
(4)14的算术平方根是 。
注意!
非平方数的算术平方根只能用根号表示。
例2:自由下落物体的高度s(m)与下落时间t(s)的关系为 。有一铁球从19.6m高的建筑物上自由下落,到达地面需要多长时间?
解:将s=19.6代入公式
,
得 ,
所以正数 (s)。
即铁球到达地面需要2s。
注意!
式子 的两层含义:
(1)a≥0;
(2) ≥0。
如果将一个长方形ABCD折叠,得到一个面积为144cm2的正方形ABFE,已知正方形ABFE的面积等于长方形CDEF面积的2倍,求长方形ABCD的长和宽。
A
B
C
D
E
F
知识拓展例题
解:设正方形ABFE的边长为a,
有 ,所以 ,
所以 。
又因为 ,设 ,
所以 , 。
所以 (cm)。
所以长方形的长为18cm,宽为
12cm。
A
B
C
D
E
F
一、填空题:1.若一个数的算术平方根是 ,那么这个数是______;
2. 的算术平方根是______;
3. 的算术平方根是______;
4.若 ,则 ____。
7
16
二、求下列各数的算术平方根:
36, ,15,0.64, , , 。
(2)因为 ,所以 的算术平方根是 ,即 ;
解:(1)因为 ,所以36的算术平方
根是6,即 ;
(3)15的算术平方根是 ;
解:(4)因为0.82=0.64,所以0.64的算术平
方根是0.8,即 ;
(5)因为 ,所以10-4的算术平方根是10-2,即 ;
(6)因为 ,所以 的算术平方根是 ;
(7)因为 ,所以 的算术平方根是1。
36, ,15,0.64, , , 。
三、如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷。若绳子的长度为5.5m,地面固定点C到帐篷支撑竿底部B的距离是4.5m,则帐篷支撑竿的高是多少?(精确到0.1m)
解:由题意得AC=5.5米,BC=4。5米,∠ABC=90°,在Rt△ ABC中,由勾股定理得:
所以帐篷支撑竿的高是3.2m。
(1)算术平方根的概念,式子 中的双重非负性:
一是a≥0,
二是 ≥0。
(2)算术平方根的性质:
一个正数的算术平方根是一个正数;
0的算术平方根是0;负数没有算术平方根。
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根。
习题4.3
作业布置
谢 谢
