专题12.2.1 三角形全等的判定1 同步导学(含解析)
文档属性
| 名称 | 专题12.2.1 三角形全等的判定1 同步导学(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 245.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
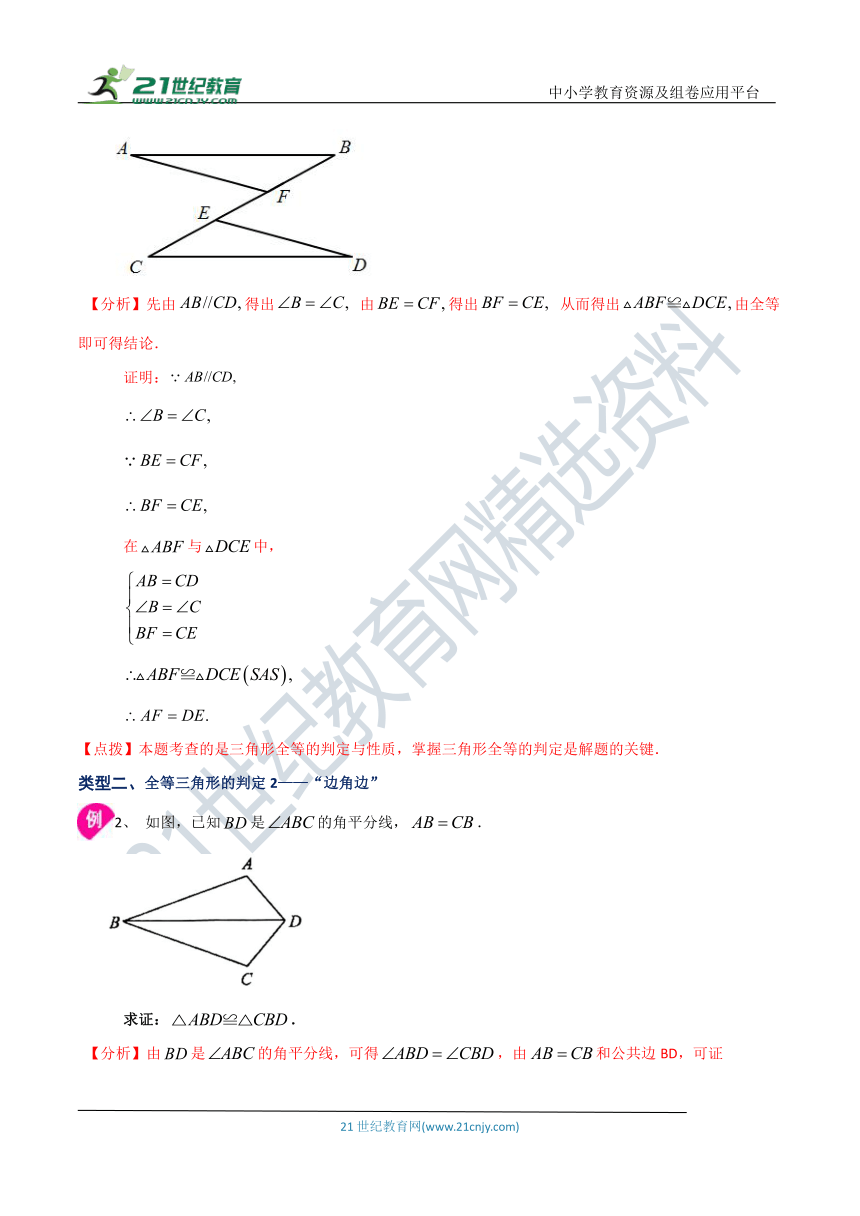
专题12.3 三角形全等的判定1(知识讲解)
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
【要点梳理】
要点一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
特别说明:如图,如果=AB,=AC,=BC,则△ABC≌△.
要点二、全等三角形判定2——“边角边”
1. 全等三角形判定2——“边角边”
两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
特别说明:如图,如果AB = ,∠A=∠,AC = ,则△ABC≌△. 注意:这里的角,指的是两组对应边的夹角.
2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.
如图,△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.
【典型例题】
类型一、全等三角形的判定1——“边边边”
1、 如图,点,,,在一条直线上,,,.
求证:(1);
(2).
【答案】(1)证明见解析;(2)证明见解析.
【分析】
(1)利用“边边边”定理证即可;
(2)由全等可得,,根据平行线的判定证明即可.
证明:(1),
,
,
在和中,
,
,
;
(2)由(1)得:,
,
.
【点拨】本题考查了全等三角形的判定与性质,平行线的判定,解题关键是依据已知条件证明三角形全等,再根据全等三角形的性质解决问题.
举一反三:
【变式】 已知:如图,,,.
求证:.
【分析】先由得出 由得出 从而得出由全等即可得结论.
证明:
在与中,
【点拨】本题考查的是三角形全等的判定与性质,掌握三角形全等的判定是解题的关键.
类型二、全等三角形的判定2——“边角边”
2、 如图,已知是的角平分线,.
求证:.
【分析】由是的角平分线,可得,由和公共边BD,可证.
证明:∵是的角平分线(已知),
∴(角平分线定义),
在与中,
∵ ,
∴.
【点拨】本题考查三角形全等证明,掌握三角形全等的证明方法是解题关键.
举一反三:
【变式】(2021·江苏淮安市·八年级期末)如图,,求证:.
【分析】直接利用全等三角形的判定方法得出答案.
证明:∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
∴在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
【点拨】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
3、如图,,,,求证:.
【分析】直接利用SAS证明,再根据全等三角形的性质即可求解;
证明:∵
∴
即
∴在与中
∴
∴
【点拨】本题考查了全等三角形的证明以及全等三角形的性质,正确掌握知识点是解题的关键;
举一反三:
【变式】(2021·云南昆明市·八年级期末)如图:已知,且,求证:.
证明:∵
∴
∴
又∵
∴
在和中
∴(SAS)
【点拨】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,
4、已知:如图,C为线段BE上一点,AB//DC,AB=EC,BC=CD. 求证:∠A=∠E .
【分析】直接利用全等三角形的判定方法得出△ABC≌△ECD,即可得出答案.
证明:∵AB∥DC,
∴∠B=∠ECD,
在△ABC和△ECD中,
,
∴△ABC≌△ECD(SAS),
∴∠A=∠E(全等三角形的对应角相等).
【点拨】此题主要考查了全等三角形的判定与性质,正确掌握全等三角形的判定方法是解题关键.
举一反三:
【变式】(2021·江苏金湖县·八年级期末)已知:如图,点A、F、E、D在同一条直线上,AB=CD,∠A=∠D,AF=DE,求证:BE∥CF.
【分析】
根据SAS证明△ABE与△DCF全等,进而利用全等三角形的性质解答即可.
证明:∵AF=DE,
∴AF+FE=DE+FE,
∴AE=DF,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠CFD=∠BEA,
∴BE∥CF.
【点拨】本题考查了全等三角形的判定和性质,正确运用三角形全等的判定方法是解题的关键.
类型三、全等三角形判定的实际应用
5、如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)求证:DE=AB;
(2)如果DE的长度是8m,则AB的长度是多少?
【答案】(1)证明见解析;(2)8m
【分析】
(1)先根据SAS证明△CDE≌△CAB,再根据全等三角形的性质即得结论;
(2)由(1)的结论结合已知即得答案.
(1)证明:在△CDE和△CAB中,
,
∴△CDE≌△CAB(SAS),
∴DE=AB;
(2)解:∵DE=AB,DE=8m,
∴AB=8m.
【点拨】本题考查了全等三角形的应用,正确理解题意、熟练掌握全等三角形的判定和性质是解题的关键.
举一反三:
【变式】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.如图1是一个四边形的木架,AB=AD=2cm,BC=5cm.
(1)扭动这个木架,四边形的形状就会改变,这说明了什么?
(2)如图2,若固定三根木条AB、BC、AD不动,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(3)在扭动这个木架过程中,当测得A、C之间的距离为6cm时,若CD的长度也是整数,那么CD的长应为多少?
【答案】(1)四边形的不稳定性;(2)相等,理由见解析;(3)CD的长应为5cm或6cm或7cm.
【分析】
(1)根据四边形的特性即可得到结论;
(2)连接AC,根据SSS证明两个三角形全等即可;
(3)根据三角形的三边关系即可得到结论.
解:(1)答:四边形的不稳定性; (2)相等.
理由:连接AC,
在△ACD和△ACB中,
,
∴△ACD≌△ACB(SSS),
∴∠B=∠D;
(3)∵AD=2,AC=6,
∴6﹣2<CD<2+6,
∴4<CD<8,
∵CD的长度也是整数,
∴CD的长应为5cm或6cm或7cm,
【点拨】本题考查了四边形的不稳定性、全等三角形的判定和性质、三角形三边关系定理等知识,熟练掌握全等三角形的判定与性质是解题的关键.
21世纪教育网(www.21cnjy.com)
专题12.3 三角形全等的判定1(知识讲解)
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
【要点梳理】
要点一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
特别说明:如图,如果=AB,=AC,=BC,则△ABC≌△.
要点二、全等三角形判定2——“边角边”
1. 全等三角形判定2——“边角边”
两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
特别说明:如图,如果AB = ,∠A=∠,AC = ,则△ABC≌△. 注意:这里的角,指的是两组对应边的夹角.
2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.
如图,△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.
【典型例题】
类型一、全等三角形的判定1——“边边边”
1、 如图,点,,,在一条直线上,,,.
求证:(1);
(2).
【答案】(1)证明见解析;(2)证明见解析.
【分析】
(1)利用“边边边”定理证即可;
(2)由全等可得,,根据平行线的判定证明即可.
证明:(1),
,
,
在和中,
,
,
;
(2)由(1)得:,
,
.
【点拨】本题考查了全等三角形的判定与性质,平行线的判定,解题关键是依据已知条件证明三角形全等,再根据全等三角形的性质解决问题.
举一反三:
【变式】 已知:如图,,,.
求证:.
【分析】先由得出 由得出 从而得出由全等即可得结论.
证明:
在与中,
【点拨】本题考查的是三角形全等的判定与性质,掌握三角形全等的判定是解题的关键.
类型二、全等三角形的判定2——“边角边”
2、 如图,已知是的角平分线,.
求证:.
【分析】由是的角平分线,可得,由和公共边BD,可证.
证明:∵是的角平分线(已知),
∴(角平分线定义),
在与中,
∵ ,
∴.
【点拨】本题考查三角形全等证明,掌握三角形全等的证明方法是解题关键.
举一反三:
【变式】(2021·江苏淮安市·八年级期末)如图,,求证:.
【分析】直接利用全等三角形的判定方法得出答案.
证明:∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
∴在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
【点拨】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
3、如图,,,,求证:.
【分析】直接利用SAS证明,再根据全等三角形的性质即可求解;
证明:∵
∴
即
∴在与中
∴
∴
【点拨】本题考查了全等三角形的证明以及全等三角形的性质,正确掌握知识点是解题的关键;
举一反三:
【变式】(2021·云南昆明市·八年级期末)如图:已知,且,求证:.
证明:∵
∴
∴
又∵
∴
在和中
∴(SAS)
【点拨】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,
4、已知:如图,C为线段BE上一点,AB//DC,AB=EC,BC=CD. 求证:∠A=∠E .
【分析】直接利用全等三角形的判定方法得出△ABC≌△ECD,即可得出答案.
证明:∵AB∥DC,
∴∠B=∠ECD,
在△ABC和△ECD中,
,
∴△ABC≌△ECD(SAS),
∴∠A=∠E(全等三角形的对应角相等).
【点拨】此题主要考查了全等三角形的判定与性质,正确掌握全等三角形的判定方法是解题关键.
举一反三:
【变式】(2021·江苏金湖县·八年级期末)已知:如图,点A、F、E、D在同一条直线上,AB=CD,∠A=∠D,AF=DE,求证:BE∥CF.
【分析】
根据SAS证明△ABE与△DCF全等,进而利用全等三角形的性质解答即可.
证明:∵AF=DE,
∴AF+FE=DE+FE,
∴AE=DF,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠CFD=∠BEA,
∴BE∥CF.
【点拨】本题考查了全等三角形的判定和性质,正确运用三角形全等的判定方法是解题的关键.
类型三、全等三角形判定的实际应用
5、如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)求证:DE=AB;
(2)如果DE的长度是8m,则AB的长度是多少?
【答案】(1)证明见解析;(2)8m
【分析】
(1)先根据SAS证明△CDE≌△CAB,再根据全等三角形的性质即得结论;
(2)由(1)的结论结合已知即得答案.
(1)证明:在△CDE和△CAB中,
,
∴△CDE≌△CAB(SAS),
∴DE=AB;
(2)解:∵DE=AB,DE=8m,
∴AB=8m.
【点拨】本题考查了全等三角形的应用,正确理解题意、熟练掌握全等三角形的判定和性质是解题的关键.
举一反三:
【变式】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.如图1是一个四边形的木架,AB=AD=2cm,BC=5cm.
(1)扭动这个木架,四边形的形状就会改变,这说明了什么?
(2)如图2,若固定三根木条AB、BC、AD不动,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(3)在扭动这个木架过程中,当测得A、C之间的距离为6cm时,若CD的长度也是整数,那么CD的长应为多少?
【答案】(1)四边形的不稳定性;(2)相等,理由见解析;(3)CD的长应为5cm或6cm或7cm.
【分析】
(1)根据四边形的特性即可得到结论;
(2)连接AC,根据SSS证明两个三角形全等即可;
(3)根据三角形的三边关系即可得到结论.
解:(1)答:四边形的不稳定性; (2)相等.
理由:连接AC,
在△ACD和△ACB中,
,
∴△ACD≌△ACB(SSS),
∴∠B=∠D;
(3)∵AD=2,AC=6,
∴6﹣2<CD<2+6,
∴4<CD<8,
∵CD的长度也是整数,
∴CD的长应为5cm或6cm或7cm,
【点拨】本题考查了四边形的不稳定性、全等三角形的判定和性质、三角形三边关系定理等知识,熟练掌握全等三角形的判定与性质是解题的关键.
21世纪教育网(www.21cnjy.com)
