5.2反比例函数的图像与性质(2)

(共16张PPT)
第五章 反比例函数
5.2 反比例函数的图象与性质（2）
小测：
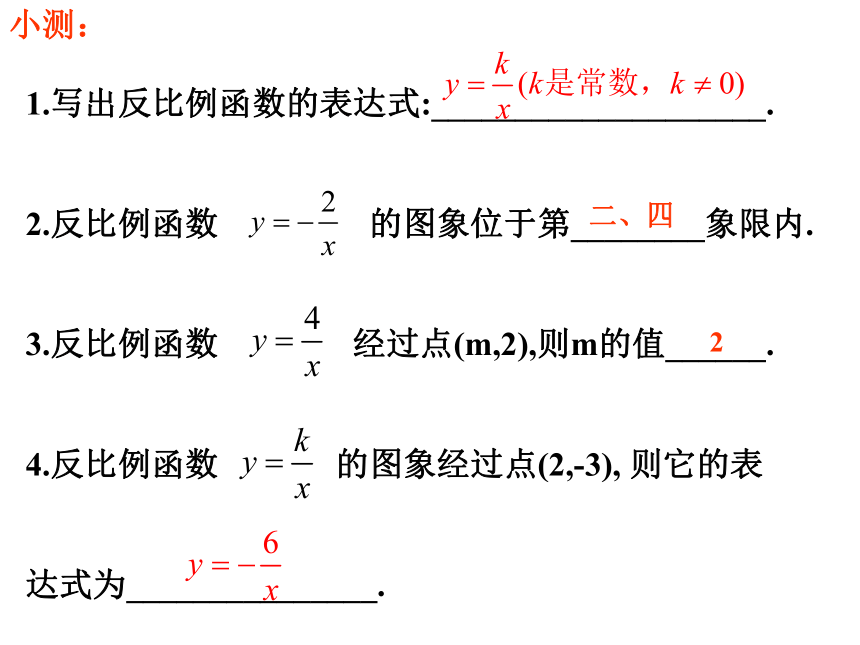
1.写出反比例函数的表达式:____________________.
2.反比例函数 的图象位于第________象限内.
3.反比例函数 经过点(m,2),则m的值______.
4.反比例函数 的图象经过点(2,-3), 则它的表
达式为_______________.
2
二、四
1.反比例函数是一个怎样的图象？
2.反比例函数的图象的位置与k有怎样关系？
当k>0时，两支曲线分别位于第一、三象限内；
当k<0时，两支曲线分别位于第二、四象限内.
反比例函数的图象是双曲线
复习回顾
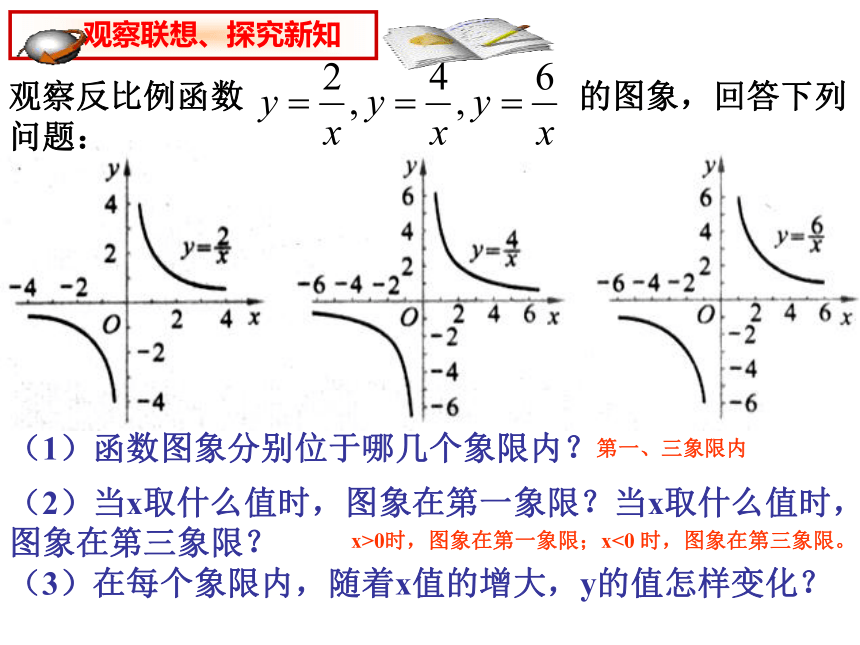
观察反比例函数 的图象，回答下列问题：
（1）函数图象分别位于哪几个象限内？
第一、三象限内
x>0时，图象在第一象限；x<0 时，图象在第三象限。
（2）当x取什么值时，图象在第一象限？当x取什么值时， 图象在第三象限？
（3）在每个象限内，随着x值的增大，y的值怎样变化？
观察联想、探究新知
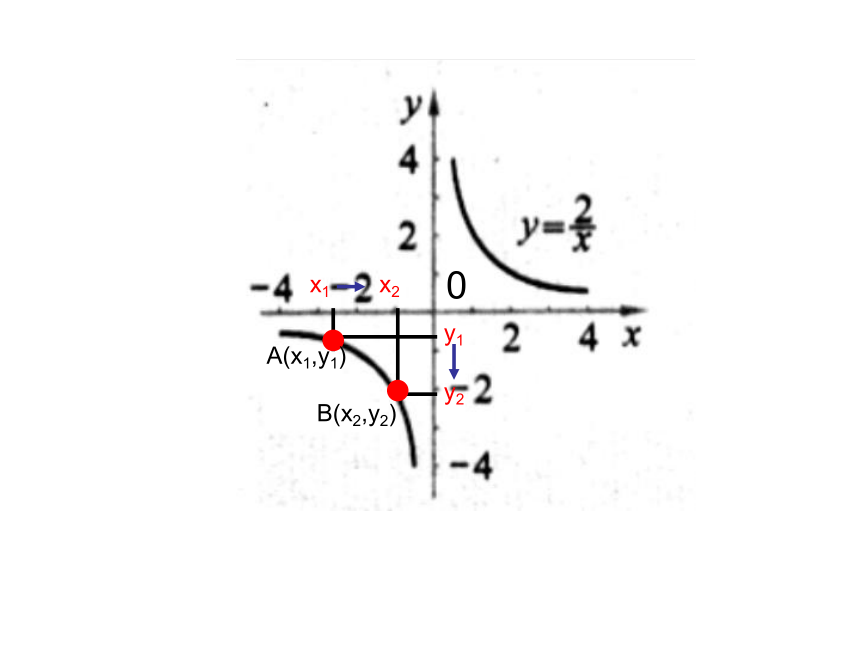
A(x1,y1)
B(x2,y2)
y2
x1
x2
y1
0
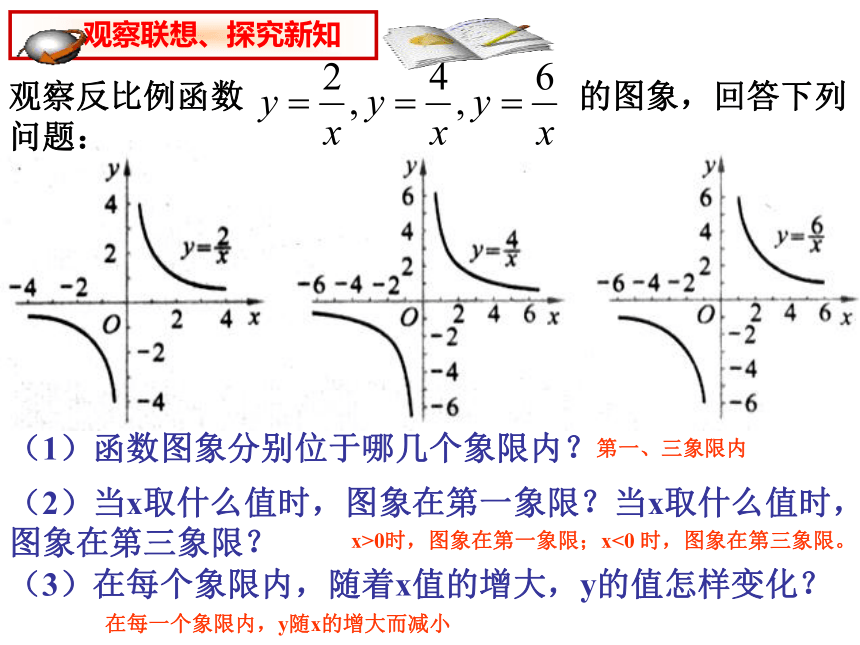
观察反比例函数 的图象，回答下列问题：
（1）函数图象分别位于哪几个象限内？
第一、三象限内
x>0时，图象在第一象限；x<0 时，图象在第三象限。
在每一个象限内，y随x的增大而减小
（2）当x取什么值时，图象在第一象限？当x取什么值时， 图象在第三象限？
（3）在每个象限内，随着x值的增大，y的值怎样变化？
观察联想、探究新知
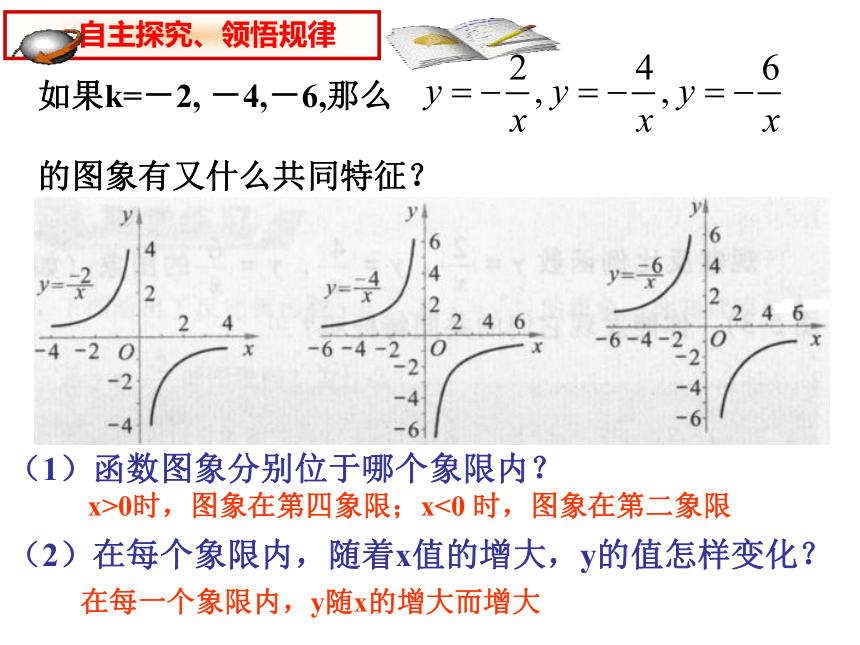
如果k=－2, －4,－6,那么
的图象有又什么共同特征？
（1）函数图象分别位于哪个象限内？
x>0时，图象在第四象限；x<0 时，图象在第二象限
（2）在每个象限内，随着x值的增大，y的值怎样变化？
在每一个象限内，y随x的增大而增大
自主探究、领悟规律
随堂练习
1.下列函数中，其图象位于第一、三象限的有____________;
在其所在的象限内，y随x的增大而增大的有___________.
（1）（2）（3）
(4)
“试金石”
2.若关于x,y的函数 图象位于第一、三象限，
则k的取值范围是_______________。
k>－1
3.甲乙两地相距100km，一辆汽车从甲地开往乙地，
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数，则这个函数的图象大致是（ ）
C
在实际问题中
图象就可能只
有一支.
P
Q
S1
S2
S1、S2有什么关系？为什么？
R
S3
S1=S2
S1、S2 、 S3有什么关系？为什么？
S1=S2= S3
想一想
在反比例函数 图象上任取三点P、Q、R，过点P、Q、R分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为S1、S2 、S3。
观察反比例函数图象的两支曲线,回答下列问题:
(1)它们会与坐标轴相交吗？
（2）反比例函数的图象是中心对称图形吗？
（3）反比例函数的图象是轴对称图形吗？
它们都不与坐标轴相交。
是轴对称图形,对称轴是y= x 。
是中心对称图形,对称中心是坐标原点。
议一议
+
_
1. 已知函数 ，在每一个象限内y随x的增大而减小，求a的值和表达式.
当函数为反比例函数时
当函数为正比例函数时……
联系拓广
1.反比例函数的性质: 反比例函数 的图象是由两条曲线组成的 ，当k>0时,图象位于第一、三象限，在每一象限内，y的值随x的增大而减小； 当k<0时，图象位于第二、四象限，y的值随x的增大而增大。
2.双曲线的两条分支逼近坐标轴但不可能与坐标轴相交。
3.反比例函数的图象是一个以原点为对称中心的中心对称图形。
4.反比例函数的图象是轴对称图形，对称轴是直线y= x
5.在反比例函数 的图象上任取一点，分别作坐标轴的垂线（或平行线），与坐标轴所围成的矩形面积 S矩形=∣K∣。
课堂小结
k
y
x
=
k
y
x
=
+
_
知识的升华
独立
作业
P155习题5.3第2、3、
4、5题.
祝你成功！
驶向胜利的彼岸
结束寄语！
下课了!
函数来自现实生活，
函数是描述现实世界
变化规律的重要数学模型。
函数的思想是一种重要的数学思想，
它是刻画两个变量之间关系的重要手段。