2021-2022学年北师大版数学九年级下册第二章 二次函数 复习与小结 (共21张ppt)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册第二章 二次函数 复习与小结 (共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 948.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 16:54:49 | ||
图片预览






文档简介
(共21张PPT)
北师大版数学九年级(下)
复习与小结
第二章 二次函数
教学过程
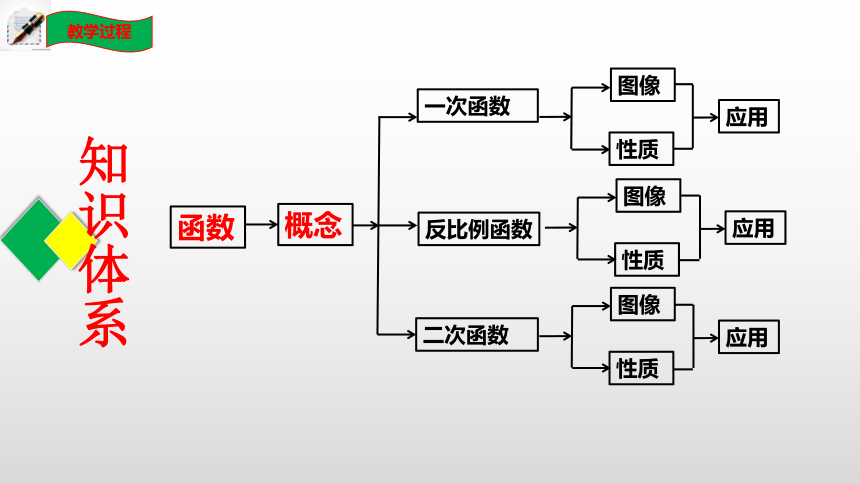
知识体系
函数
一次函数
反比例函数
二次函数
图像
应用
概念
性质
图像
性质
图像
性质
应用
应用
教学过程
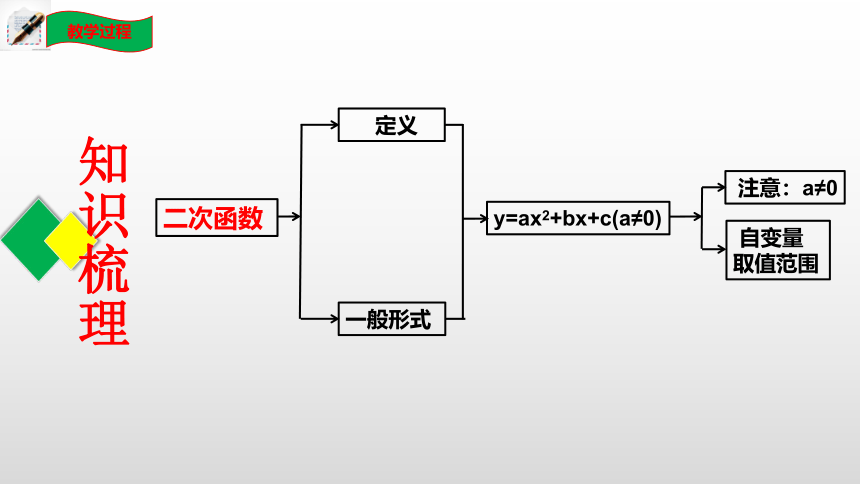
知识梳理
二次函数
定义
一般形式
y=ax2+bx+c(a≠0)
注意:a≠0
自变量取值范围
教学过程
知识梳理
二次函的图像及表达式
图像
三种表达式
一般式:y=ax2+bx+c(a≠0)
抛物线
顶点式:y=a(x-h)2+k(a≠0)
交点式:y=a(x-x1)(x-x2)(a≠0)
教学过程
知识梳理
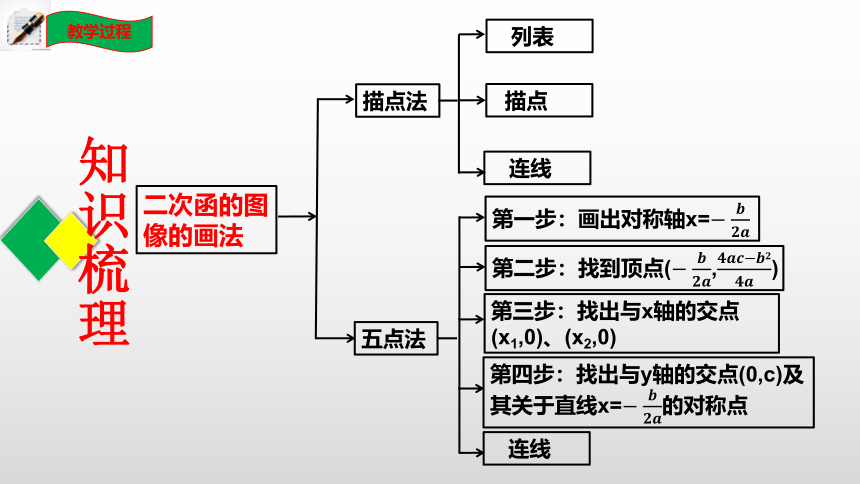
二次函的图像的画法
描点法
五点法
第一步:画出对称轴x=
列表
第二步:找到顶点(,)
第三步:找出与x轴的交点(x1,0)、(x2,0)
第四步:找出与y轴的交点(0,c)及其关于直线x=的对称点
描点
连线
连线
教学过程
知识梳理
二次函数的平移
y=a(x-h)2+k
y=ax2
h=
向右移h个单
向左移个单位
k=
向上移k个单位
向下移个单位
y=ax2+bx+c
h>0
h<0
k>0
k<0
教学过程
知识梳理
二次函数的性质
开口方:a>0开口向上,a<0开口向下
对称轴:x= 或x=h
顶点:(,)或(h,k)
极值:当x=时,y极值= 或x=h时,y极值=k
增减性:a>0,对称轴左侧,y随x的增大而减小;对称轴右侧,y随x的增大而增大。
a<0,对称轴左侧,y随x的增大而增大;对称轴右侧,y随x的增大而减小。
教学过程
知识梳理
二次函数的确定
待定系数法
三点坐标
一般式:y=ax2+bx+c(a≠0)
顶点坐标
与x轴交点坐标
交点式:y=a(x-x1)(x-x2)(a≠0)
顶点式:y=a(x-h)2+k(a≠0)
教学过程
知识梳理
二次函数的应用
抛物线问题
面积相关问题
利润相关问题
建立适当坐标系
利用利润公式,建立二次函数模型
面积问题转化为二次函数问题
二次函数与一元二次方程
教学过程
知识梳理
抛物线x轴交点
一元二次方程近似根
b2-4ac>0,两个交点
b2-4ac=0,一个交点
b2-4ac<0,没有交点
教学过程
基础训练
1.若函数 y=(1 m)x 7+2是关于x的二次函数,且其图象的开口向上,则m的值为
( )
A.-2 B.-1 C.-3 D.3
C
2.二次函数 y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中 0①abc>0; ② 3④a-b >am2+bm(m≠ 1);(5)a>.其中正确的结论有( )
教学过程
基础训练
x=-1
C
A.5个
B.4个
C.3个
D.2个
教学过程
基础应用
3.已知二次函数 y=x2 3(m 1)x+3m-4(m为实数)的图象与x轴交于A(x1,0)、B(x2,0) (x1≠x2)两点.
(1)求m的取值范围;
(2)若 += (O为坐标原点),求m的值
解:(1)∵二次函数 y=x2 3(m 1)x+3m 4(m为实数)的图象与x轴有两个交点,
教学过程
基础应用
∴△=9(m 1)2 4(3m 4)>0.
化简、整理,得 (3m 5)2>0,
解得 m ≠ .
(2)根据题意,得x1、x2为方程 的两根,
∴x1+x2=3(m 1),x1x2=3m 4.,
∵ += , ∴=
教学过程
基础应用
∴OA+OB=2.
∵OA=∣x1∣,OB=∣x2∣,
∴∣x1∣+∣x2∣=2
①当方程的两根同为正数时,由 ∣x1∣+∣x2∣=2,
得 x1+x2=2,即3(m-1)=2.
②当方程的两根同为负数时,由 ∣x1∣+∣x2∣=2,
得 x1+x2=-2,即3(m-1)=-2.
由. 解得m= (舍去)
教学过程
基础应用
由. 无解
③当方程的两根异号时由 ,
得 .
将两边同时平方,得
,得
,解得
综上所述,m的值为1.
4.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,那么销售单价应控制在什么范围内?
教学过程
综合应用
解:(1)由题意,得y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
= 5x2+800x 27500,
即 y= 5x2+800x-27500(50≤x≤100).
教学过程
综合应用
(2)y= 5x2+800x 27500= 5(x 80)2+4500.
∵a=-5<0,
∴抛物线开口向下.
.∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500.
教学过程
综合应用
(3)当y=4000时,一5(x-80)2+4500=4000,解得
x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
教学过程
巩固练习
完成练习册相关作业.
谢谢观看
教学过程
新课结束
北师大版数学九年级(下)
复习与小结
第二章 二次函数
教学过程
知识体系
函数
一次函数
反比例函数
二次函数
图像
应用
概念
性质
图像
性质
图像
性质
应用
应用
教学过程
知识梳理
二次函数
定义
一般形式
y=ax2+bx+c(a≠0)
注意:a≠0
自变量取值范围
教学过程
知识梳理
二次函的图像及表达式
图像
三种表达式
一般式:y=ax2+bx+c(a≠0)
抛物线
顶点式:y=a(x-h)2+k(a≠0)
交点式:y=a(x-x1)(x-x2)(a≠0)
教学过程
知识梳理
二次函的图像的画法
描点法
五点法
第一步:画出对称轴x=
列表
第二步:找到顶点(,)
第三步:找出与x轴的交点(x1,0)、(x2,0)
第四步:找出与y轴的交点(0,c)及其关于直线x=的对称点
描点
连线
连线
教学过程
知识梳理
二次函数的平移
y=a(x-h)2+k
y=ax2
h=
向右移h个单
向左移个单位
k=
向上移k个单位
向下移个单位
y=ax2+bx+c
h>0
h<0
k>0
k<0
教学过程
知识梳理
二次函数的性质
开口方:a>0开口向上,a<0开口向下
对称轴:x= 或x=h
顶点:(,)或(h,k)
极值:当x=时,y极值= 或x=h时,y极值=k
增减性:a>0,对称轴左侧,y随x的增大而减小;对称轴右侧,y随x的增大而增大。
a<0,对称轴左侧,y随x的增大而增大;对称轴右侧,y随x的增大而减小。
教学过程
知识梳理
二次函数的确定
待定系数法
三点坐标
一般式:y=ax2+bx+c(a≠0)
顶点坐标
与x轴交点坐标
交点式:y=a(x-x1)(x-x2)(a≠0)
顶点式:y=a(x-h)2+k(a≠0)
教学过程
知识梳理
二次函数的应用
抛物线问题
面积相关问题
利润相关问题
建立适当坐标系
利用利润公式,建立二次函数模型
面积问题转化为二次函数问题
二次函数与一元二次方程
教学过程
知识梳理
抛物线x轴交点
一元二次方程近似根
b2-4ac>0,两个交点
b2-4ac=0,一个交点
b2-4ac<0,没有交点
教学过程
基础训练
1.若函数 y=(1 m)x 7+2是关于x的二次函数,且其图象的开口向上,则m的值为
( )
A.-2 B.-1 C.-3 D.3
C
2.二次函数 y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中 0
教学过程
基础训练
x=-1
C
A.5个
B.4个
C.3个
D.2个
教学过程
基础应用
3.已知二次函数 y=x2 3(m 1)x+3m-4(m为实数)的图象与x轴交于A(x1,0)、B(x2,0) (x1≠x2)两点.
(1)求m的取值范围;
(2)若 += (O为坐标原点),求m的值
解:(1)∵二次函数 y=x2 3(m 1)x+3m 4(m为实数)的图象与x轴有两个交点,
教学过程
基础应用
∴△=9(m 1)2 4(3m 4)>0.
化简、整理,得 (3m 5)2>0,
解得 m ≠ .
(2)根据题意,得x1、x2为方程 的两根,
∴x1+x2=3(m 1),x1x2=3m 4.,
∵ += , ∴=
教学过程
基础应用
∴OA+OB=2.
∵OA=∣x1∣,OB=∣x2∣,
∴∣x1∣+∣x2∣=2
①当方程的两根同为正数时,由 ∣x1∣+∣x2∣=2,
得 x1+x2=2,即3(m-1)=2.
②当方程的两根同为负数时,由 ∣x1∣+∣x2∣=2,
得 x1+x2=-2,即3(m-1)=-2.
由. 解得m= (舍去)
教学过程
基础应用
由. 无解
③当方程的两根异号时由 ,
得 .
将两边同时平方,得
,得
,解得
综上所述,m的值为1.
4.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,那么销售单价应控制在什么范围内?
教学过程
综合应用
解:(1)由题意,得y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
= 5x2+800x 27500,
即 y= 5x2+800x-27500(50≤x≤100).
教学过程
综合应用
(2)y= 5x2+800x 27500= 5(x 80)2+4500.
∵a=-5<0,
∴抛物线开口向下.
.∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500.
教学过程
综合应用
(3)当y=4000时,一5(x-80)2+4500=4000,解得
x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
教学过程
巩固练习
完成练习册相关作业.
谢谢观看
教学过程
新课结束
