2021-2022学年高一下学期数学北师大版(2019)必修第二册1.3弧度制课件(共32张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册1.3弧度制课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 752.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 22:46:26 | ||
图片预览










文档简介
(共32张PPT)
§ 1.3 弧度制
北师大(2019)必修2
琪
胡
聚焦知识目标
1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集一一对应关系
3.掌握并能应用弧度制下的弧长公式和扇形面积公式.
数学素养
1.通过弧度制的建立过程,培养逻辑推理素养.
2.通过弧度制与角度制的换算以及弧长公式和扇形的面积公式的应用,提升数学运算素养.
环节一
复习角度制
复习角度制
角的终边的旋转方向
零角
负角
正角
→ 正的角度数
→ 负的角度数
→ 0°
比如: 30°, 600°
比如:-30°,-600°
一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形
任意角
1°是如何定义的?
六十进制
角度制
思考
我们能否寻找一种更为便利的度量角的大小的量呢?
长度可以用米、厘米、英尺、码等不同的单位度量,物体的重量可以用千克、磅等不同的单位度量.不同的单位制能给解决问题带来方便,以度为单位度量角的大小是一种常用方法,为了进一步研究的需要,我们还需建立一个度量角的单位制.
环节二
弧度制的概念
弧度制的概念
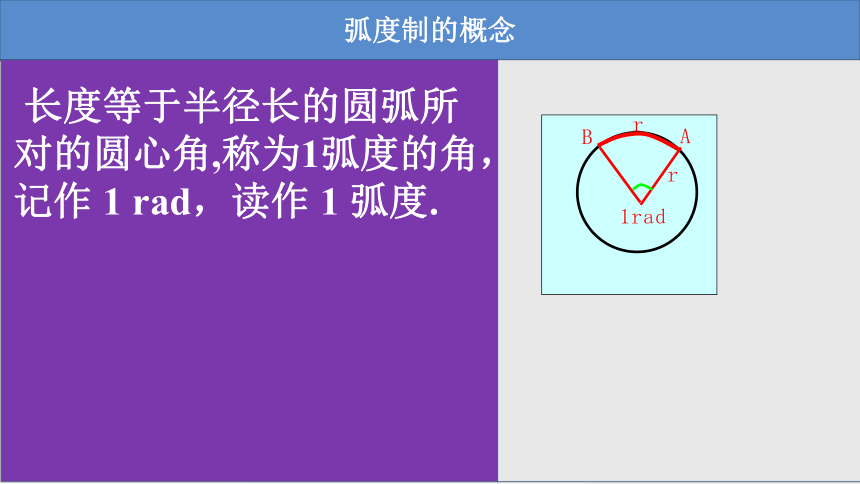
长度等于半径长的圆弧所对的圆心角,称为1弧度的角,记作 1 rad,读作 1 弧度.
1rad
A
B
r
r
弧度制的概念
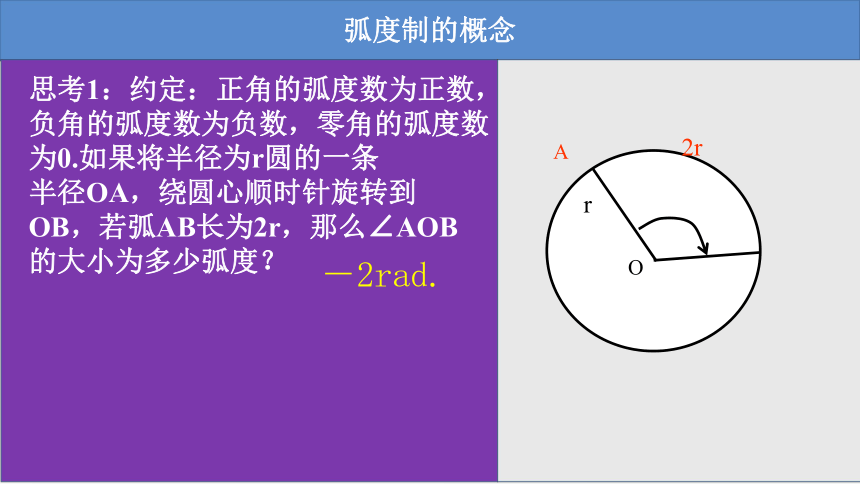
思考1:约定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数
为0.如果将半径为r圆的一条
半径OA,绕圆心顺时针旋转到
OB,若弧AB长为2r,那么∠AOB
的大小为多少弧度?
O
A
r
2r
-2rad.
弧度制的概念
思考2:如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值如何计算?
O
A
r
B
l
环节三
弧度制与角度制转化
弧度制与角度制的互化
请填写下面的表格并思考:如图,半径为r的圆,圆心与原点重合,角的始边与轴的非负半轴重合,交圆于点A,终边与圆交于点B,填写下表:
OB旋转的方向
逆时针方向
逆时针方向
逆时针方向
顺时针方向
0 未旋转
弧度制与角度制的互化
思考1:一个圆周角以度为单位度量是多少度?以弧度为单位度量是多少弧度?由此可得度与弧度有怎样的换算关系?
思考2:根据上述关系,1°等于多少弧度?1rad等于多少度?
弧度制与角度制的互化
思考3:根据度与弧度的换算关系,下表中各特殊角对应的弧度数分别是多少?
角度
弧度
弧度制与角度制的互化
例1 把下列各角化为角度与弧度
答案:
弧度制与角度制的互化
练习1 把下列各角化为角度与弧度
答案:
弧度制与角度制的互化
练习2 写出下列各组角度所对应的弧度
环节四
弧长公式和扇形面积公式
弧长公式和扇形面积公式
已知一个扇形所在圆的半径为R,弧长为l,圆心角为α那么扇形的弧长公式和面积如何计算?
弧长公式和扇形面积公式
已知一个扇形所在圆的半径为R,弧长为l,圆心角为α那么扇形的弧长公式和面积如何计算?
弧长公式和扇形面积公式
解 设扇形的圆心角为θ,半径为r,弧长为l,面积为S,
则l+2r=40,∴l=40-2r.
例2 已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
∴当半径r=10 cm时,扇形的面积最大,最大值为100 cm2,
所以当扇形的圆心角为2 rad,半径为10 cm时,扇形的面积最大为100 cm2.
弧长公式和扇形面积公式
例2 已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
灵活运用扇形弧长公式、面积公式列方程组求解是解决此类问题的关键,有时运用函数思想、转化思想解决扇形中的有关最值问题,将扇形面积表示为半径的函数,转化为r的二次函数的最值问题.
所以当扇形的圆心角为2 rad,半径为10 cm时,扇形的面积最大为100 cm2.
弧长公式和扇形面积公式
练习3:(1)已知扇形的圆心角为60°,半径为3,求圆心角所对弧长及扇形面积。
弧长公式和扇形面积公式
练习3:(2)已知扇形的弧长为10,半径为5,求圆心角及扇形面积.
思考:弦AB的长度为多少?
环节五
反思与学习
检测
检测
检测
检测
课堂小结
1.核心要点
1.弧度制的概念
2.角度制与弧度制的互化
3.弧长公式、扇形面积公式
特殊角的
弧度数
在弧度制中,弧度单位rad 可以省略不写。
角的集合与实数集合建立一一对应关系,即.
课堂小结
2.数学素养
1.通过弧度制的建立过程,培养逻辑推理素养.
2.通过弧度制与角度制的换算以及弧长公式和扇形的面积公式的应用,提升数学运算素养.
胡琪老师制作
§ 1.3 弧度制
北师大(2019)必修2
琪
胡
聚焦知识目标
1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集一一对应关系
3.掌握并能应用弧度制下的弧长公式和扇形面积公式.
数学素养
1.通过弧度制的建立过程,培养逻辑推理素养.
2.通过弧度制与角度制的换算以及弧长公式和扇形的面积公式的应用,提升数学运算素养.
环节一
复习角度制
复习角度制
角的终边的旋转方向
零角
负角
正角
→ 正的角度数
→ 负的角度数
→ 0°
比如: 30°, 600°
比如:-30°,-600°
一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形
任意角
1°是如何定义的?
六十进制
角度制
思考
我们能否寻找一种更为便利的度量角的大小的量呢?
长度可以用米、厘米、英尺、码等不同的单位度量,物体的重量可以用千克、磅等不同的单位度量.不同的单位制能给解决问题带来方便,以度为单位度量角的大小是一种常用方法,为了进一步研究的需要,我们还需建立一个度量角的单位制.
环节二
弧度制的概念
弧度制的概念
长度等于半径长的圆弧所对的圆心角,称为1弧度的角,记作 1 rad,读作 1 弧度.
1rad
A
B
r
r
弧度制的概念
思考1:约定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数
为0.如果将半径为r圆的一条
半径OA,绕圆心顺时针旋转到
OB,若弧AB长为2r,那么∠AOB
的大小为多少弧度?
O
A
r
2r
-2rad.
弧度制的概念
思考2:如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值如何计算?
O
A
r
B
l
环节三
弧度制与角度制转化
弧度制与角度制的互化
请填写下面的表格并思考:如图,半径为r的圆,圆心与原点重合,角的始边与轴的非负半轴重合,交圆于点A,终边与圆交于点B,填写下表:
OB旋转的方向
逆时针方向
逆时针方向
逆时针方向
顺时针方向
0 未旋转
弧度制与角度制的互化
思考1:一个圆周角以度为单位度量是多少度?以弧度为单位度量是多少弧度?由此可得度与弧度有怎样的换算关系?
思考2:根据上述关系,1°等于多少弧度?1rad等于多少度?
弧度制与角度制的互化
思考3:根据度与弧度的换算关系,下表中各特殊角对应的弧度数分别是多少?
角度
弧度
弧度制与角度制的互化
例1 把下列各角化为角度与弧度
答案:
弧度制与角度制的互化
练习1 把下列各角化为角度与弧度
答案:
弧度制与角度制的互化
练习2 写出下列各组角度所对应的弧度
环节四
弧长公式和扇形面积公式
弧长公式和扇形面积公式
已知一个扇形所在圆的半径为R,弧长为l,圆心角为α那么扇形的弧长公式和面积如何计算?
弧长公式和扇形面积公式
已知一个扇形所在圆的半径为R,弧长为l,圆心角为α那么扇形的弧长公式和面积如何计算?
弧长公式和扇形面积公式
解 设扇形的圆心角为θ,半径为r,弧长为l,面积为S,
则l+2r=40,∴l=40-2r.
例2 已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
∴当半径r=10 cm时,扇形的面积最大,最大值为100 cm2,
所以当扇形的圆心角为2 rad,半径为10 cm时,扇形的面积最大为100 cm2.
弧长公式和扇形面积公式
例2 已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
灵活运用扇形弧长公式、面积公式列方程组求解是解决此类问题的关键,有时运用函数思想、转化思想解决扇形中的有关最值问题,将扇形面积表示为半径的函数,转化为r的二次函数的最值问题.
所以当扇形的圆心角为2 rad,半径为10 cm时,扇形的面积最大为100 cm2.
弧长公式和扇形面积公式
练习3:(1)已知扇形的圆心角为60°,半径为3,求圆心角所对弧长及扇形面积。
弧长公式和扇形面积公式
练习3:(2)已知扇形的弧长为10,半径为5,求圆心角及扇形面积.
思考:弦AB的长度为多少?
环节五
反思与学习
检测
检测
检测
检测
课堂小结
1.核心要点
1.弧度制的概念
2.角度制与弧度制的互化
3.弧长公式、扇形面积公式
特殊角的
弧度数
在弧度制中,弧度单位rad 可以省略不写。
角的集合与实数集合建立一一对应关系,即.
课堂小结
2.数学素养
1.通过弧度制的建立过程,培养逻辑推理素养.
2.通过弧度制与角度制的换算以及弧长公式和扇形的面积公式的应用,提升数学运算素养.
胡琪老师制作
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
