小学数学苏教版六年级下二 圆柱和圆锥 练习二 课件(共23张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下二 圆柱和圆锥 练习二 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
圆柱和圆锥
练习二
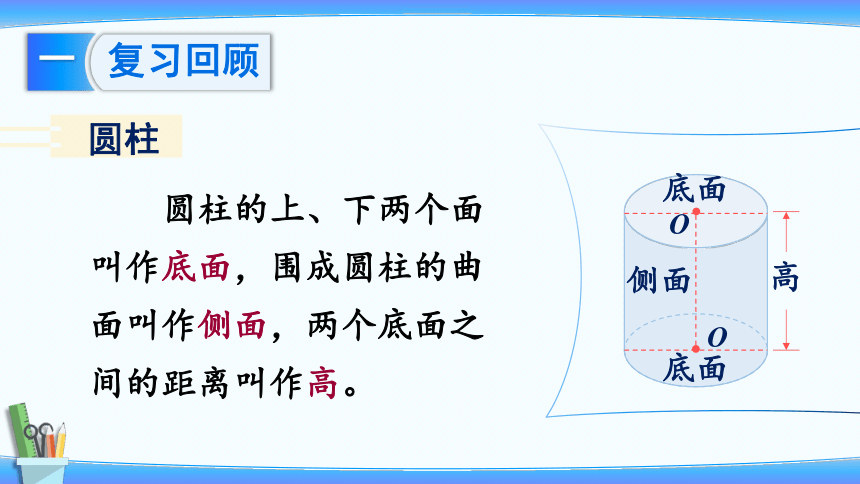
圆柱
底面
底面
侧面
O
O
高
圆柱的上、下两个面叫作底面,围成圆柱的曲面叫作侧面,两个底面之间的距离叫作高。
圆锥
圆锥只有一个底面,是圆形;圆锥的侧面是一个曲面;从圆锥的顶点到底面圆心的距离是圆锥的高。
顶点
底面
O
高
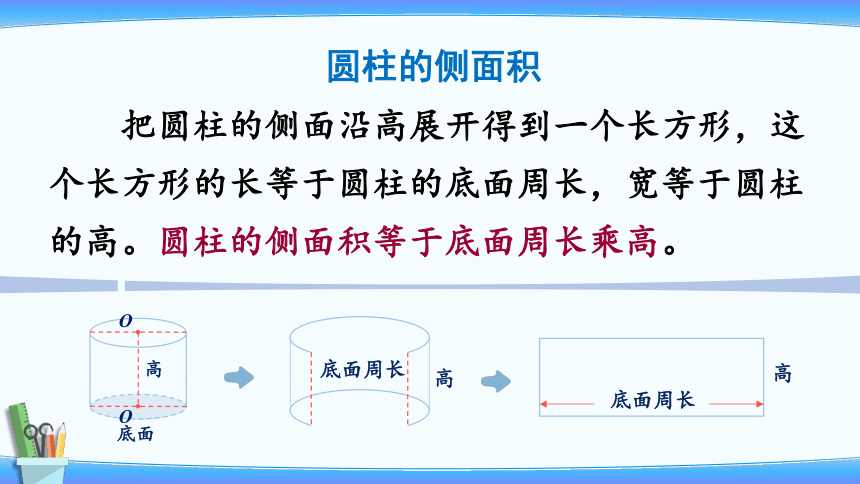
把圆柱的侧面沿高展开得到一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。圆柱的侧面积等于底面周长乘高。
底面
O
O
高
底面周长
高
底面周长
高
圆柱的侧面积
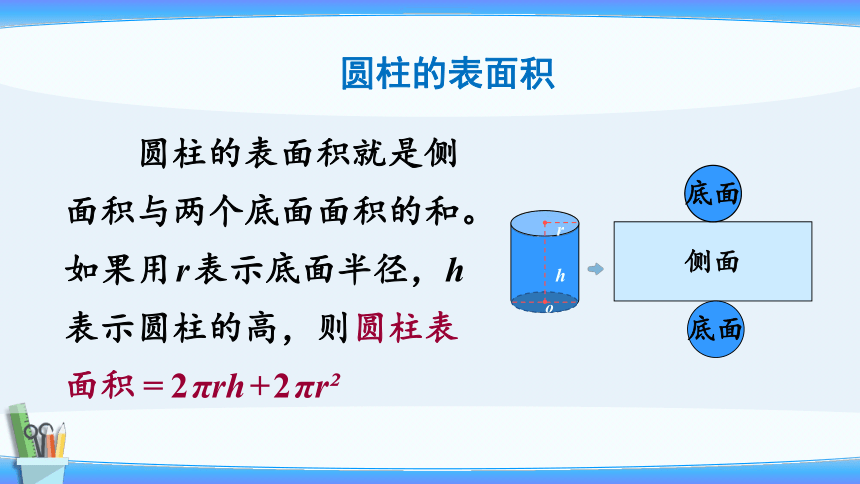
圆柱的表面积
圆柱的表面积就是侧面积与两个底面面积的和。如果用r表示底面半径,h表示圆柱的高,则圆柱表面积=2πrh+2πr
侧面
底面
底面
h
r
o
(教科书第13页~14页)
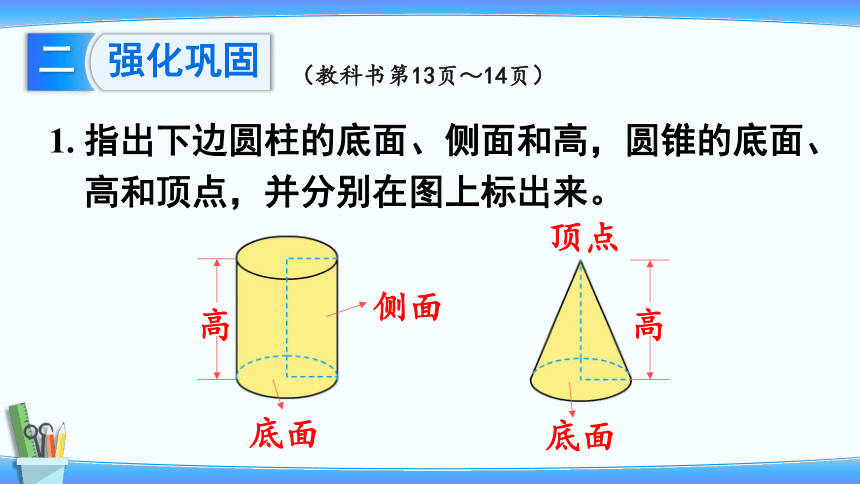
1. 指出下边圆柱的底面、侧面和高,圆锥的底面、
高和顶点,并分别在图上标出来。
高
底面
侧面
顶点
底面
高
前面
上面
右面
前面
上面
右面
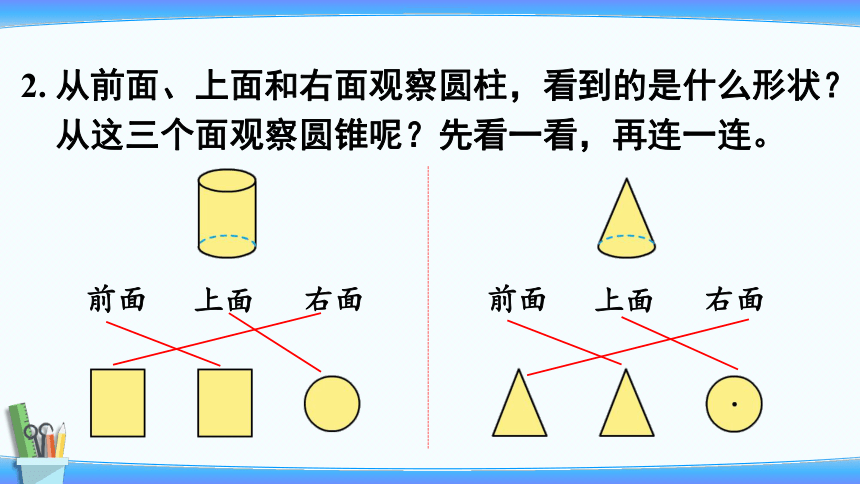
2. 从前面、上面和右面观察圆柱,看到的是什么形状?
从这三个面观察圆锥呢?先看一看,再连一连。
3. 剪下第113页、115页的图形,分别做一个圆柱
和一个圆锥,量出它们的底面直径和高,并算
出底面周长和底面积。
提示:根据实际测量的数据,分别算出底面周长和底面积。
4. 少先队队鼓是圆柱形的,侧面由铝皮围成,上、
下底面蒙的是羊皮。做这样一个队鼓,
至少需要铝皮多少平方分米?羊皮呢?
铝皮:6×3.14×2.6=48.984(平方分米)
羊皮:(6÷2) ×3.14×2=56.52(平方分米)
答:至少需要铝皮48.984平方分米,羊皮56.52
平方分米。
5. 一个圆柱形油桶,底面直径是0.6米,
高是1米。做这个油桶至少需要铁皮
多少平方米?(得数保留两位小数)
0.6×3.14×1+(0.6÷2) ×3.14×2≈2.45(平方米)
答:做这个油桶至少需要铁皮2.45平方米。
6. 算一算,填一填。
圆柱 底面半径 底面直径 高 侧面积 底面积 表面积
4cm 5cm
10cm 10cm
8cm
5cm
125.6cm
50.24cm
226.08cm
314cm
78.5
cm
471
cm
7. 用白铁皮做一根长2米、管口直径0.15米的圆
柱形通风管(如右图),至少需要白铁皮多少
平方米?
0.15×3.14×2=0.942(平方米)
答:至少需要白铁皮0.942平方米。
8. 制作一个底面直径24厘米、高30厘米
的圆柱形灯笼(如右图),在它的下
底面和侧面糊上彩纸,至少需要彩纸
多少平方厘米?
24×3.14×30+(24÷2) ×3.14
=2712.96(平方厘米)
答:至少需要彩纸2712.96平方厘米。
9. 一个圆柱形铁皮水桶,上面没有盖,高是6分
米,底面半径是1.8分米。做这个水桶大约要
用铁皮多少平方分米?
1.8×2×3.14×6+1.8 ×3.14=77.9976(平方分米)
答:做这个水桶大约要用铁皮77.9976平方分米。
10. 右图的“博士帽”是用黑色卡纸做成的,上面是
边长30厘米的正方形,下面是底面直径
16厘米、高10厘米的无底无盖的圆柱。
制作20顶这样的“博士帽”,至少需要多少平方分米的黑色卡纸?
分析:“博士帽”的面积包括帽顶正方形的面积和下面圆柱的侧面积。
(30×30+3.14×16×10)×20=28048(平方厘米)
答:至少需要黑色卡纸280.48平方分米。
28048平方厘米=280.48平方分米
先求一顶“博士帽”需要黑色卡纸的面积,再求20顶需要多少卡纸。
11. 广场上有一根花柱,高3.5米,底面半径0.5米,
花柱的侧面和上面插满塑料花。如果每平方
米有40朵花,这根花柱上面一共有多少朵花?
3.14×2×0.5×3.5+3.14×(0.5)
=11.775(平方米)
答:这根花柱上面一共有471朵花。
11.775×40=471(朵)
12.
给5根这样的珠子刷油漆,每平方米用油漆0.5千克,一共要用油漆多少千克?
答:一共要用油漆23.55千克。
3.14×3×5×0.5=23.55(千克)
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是
圆柱。截开后,表面积增加多少平方厘米?
向这样截成4段、5段呢?
分析:一根圆柱截成3段,需要截2次,每截一次会多出2个圆面,所以表面积增加2个底面圆的面积,把它截成3段,表面积比原来增加4个底面圆的面积。
截成4段、5段表面积分别比原来增加6个、8个底面圆的面积。
截成3段表面积增加:
截成4段表面积增加:
截成5段表面积增加:
3.14×(20÷2) ×4=1256(平方厘米)
3.14×(20÷2) ×6=1884(平方厘米)
3.14×(20÷2) ×8=2512(平方厘米)
解题时要区分圆柱的侧面积与表面积,根据相应的计算公式求所要求的量。
把一个圆柱截成n个小圆柱时,表面积会增加2(n 1)个圆柱底面圆的面积。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
圆柱和圆锥
练习二
圆柱
底面
底面
侧面
O
O
高
圆柱的上、下两个面叫作底面,围成圆柱的曲面叫作侧面,两个底面之间的距离叫作高。
圆锥
圆锥只有一个底面,是圆形;圆锥的侧面是一个曲面;从圆锥的顶点到底面圆心的距离是圆锥的高。
顶点
底面
O
高
把圆柱的侧面沿高展开得到一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。圆柱的侧面积等于底面周长乘高。
底面
O
O
高
底面周长
高
底面周长
高
圆柱的侧面积
圆柱的表面积
圆柱的表面积就是侧面积与两个底面面积的和。如果用r表示底面半径,h表示圆柱的高,则圆柱表面积=2πrh+2πr
侧面
底面
底面
h
r
o
(教科书第13页~14页)
1. 指出下边圆柱的底面、侧面和高,圆锥的底面、
高和顶点,并分别在图上标出来。
高
底面
侧面
顶点
底面
高
前面
上面
右面
前面
上面
右面
2. 从前面、上面和右面观察圆柱,看到的是什么形状?
从这三个面观察圆锥呢?先看一看,再连一连。
3. 剪下第113页、115页的图形,分别做一个圆柱
和一个圆锥,量出它们的底面直径和高,并算
出底面周长和底面积。
提示:根据实际测量的数据,分别算出底面周长和底面积。
4. 少先队队鼓是圆柱形的,侧面由铝皮围成,上、
下底面蒙的是羊皮。做这样一个队鼓,
至少需要铝皮多少平方分米?羊皮呢?
铝皮:6×3.14×2.6=48.984(平方分米)
羊皮:(6÷2) ×3.14×2=56.52(平方分米)
答:至少需要铝皮48.984平方分米,羊皮56.52
平方分米。
5. 一个圆柱形油桶,底面直径是0.6米,
高是1米。做这个油桶至少需要铁皮
多少平方米?(得数保留两位小数)
0.6×3.14×1+(0.6÷2) ×3.14×2≈2.45(平方米)
答:做这个油桶至少需要铁皮2.45平方米。
6. 算一算,填一填。
圆柱 底面半径 底面直径 高 侧面积 底面积 表面积
4cm 5cm
10cm 10cm
8cm
5cm
125.6cm
50.24cm
226.08cm
314cm
78.5
cm
471
cm
7. 用白铁皮做一根长2米、管口直径0.15米的圆
柱形通风管(如右图),至少需要白铁皮多少
平方米?
0.15×3.14×2=0.942(平方米)
答:至少需要白铁皮0.942平方米。
8. 制作一个底面直径24厘米、高30厘米
的圆柱形灯笼(如右图),在它的下
底面和侧面糊上彩纸,至少需要彩纸
多少平方厘米?
24×3.14×30+(24÷2) ×3.14
=2712.96(平方厘米)
答:至少需要彩纸2712.96平方厘米。
9. 一个圆柱形铁皮水桶,上面没有盖,高是6分
米,底面半径是1.8分米。做这个水桶大约要
用铁皮多少平方分米?
1.8×2×3.14×6+1.8 ×3.14=77.9976(平方分米)
答:做这个水桶大约要用铁皮77.9976平方分米。
10. 右图的“博士帽”是用黑色卡纸做成的,上面是
边长30厘米的正方形,下面是底面直径
16厘米、高10厘米的无底无盖的圆柱。
制作20顶这样的“博士帽”,至少需要多少平方分米的黑色卡纸?
分析:“博士帽”的面积包括帽顶正方形的面积和下面圆柱的侧面积。
(30×30+3.14×16×10)×20=28048(平方厘米)
答:至少需要黑色卡纸280.48平方分米。
28048平方厘米=280.48平方分米
先求一顶“博士帽”需要黑色卡纸的面积,再求20顶需要多少卡纸。
11. 广场上有一根花柱,高3.5米,底面半径0.5米,
花柱的侧面和上面插满塑料花。如果每平方
米有40朵花,这根花柱上面一共有多少朵花?
3.14×2×0.5×3.5+3.14×(0.5)
=11.775(平方米)
答:这根花柱上面一共有471朵花。
11.775×40=471(朵)
12.
给5根这样的珠子刷油漆,每平方米用油漆0.5千克,一共要用油漆多少千克?
答:一共要用油漆23.55千克。
3.14×3×5×0.5=23.55(千克)
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是
圆柱。截开后,表面积增加多少平方厘米?
向这样截成4段、5段呢?
分析:一根圆柱截成3段,需要截2次,每截一次会多出2个圆面,所以表面积增加2个底面圆的面积,把它截成3段,表面积比原来增加4个底面圆的面积。
截成4段、5段表面积分别比原来增加6个、8个底面圆的面积。
截成3段表面积增加:
截成4段表面积增加:
截成5段表面积增加:
3.14×(20÷2) ×4=1256(平方厘米)
3.14×(20÷2) ×6=1884(平方厘米)
3.14×(20÷2) ×8=2512(平方厘米)
解题时要区分圆柱的侧面积与表面积,根据相应的计算公式求所要求的量。
把一个圆柱截成n个小圆柱时,表面积会增加2(n 1)个圆柱底面圆的面积。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
