小学数学苏教版六年级下二 圆柱和圆锥 练习三 课件(共30张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下二 圆柱和圆锥 练习三 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 07:34:07 | ||
图片预览


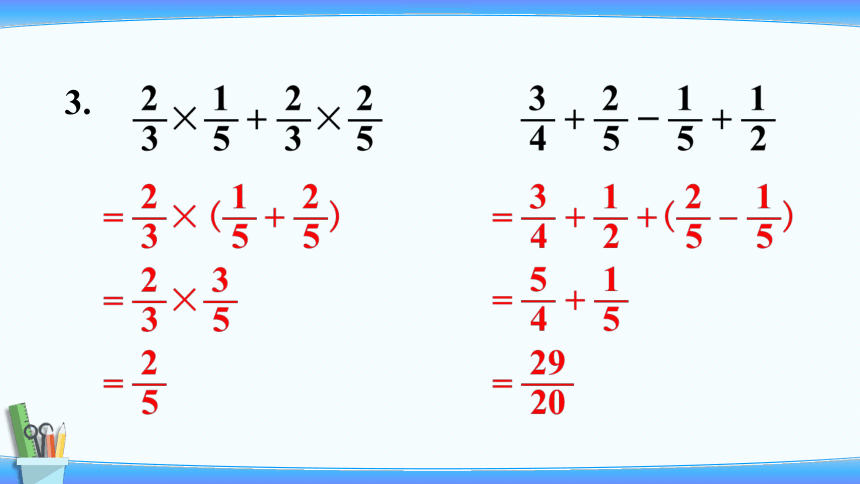
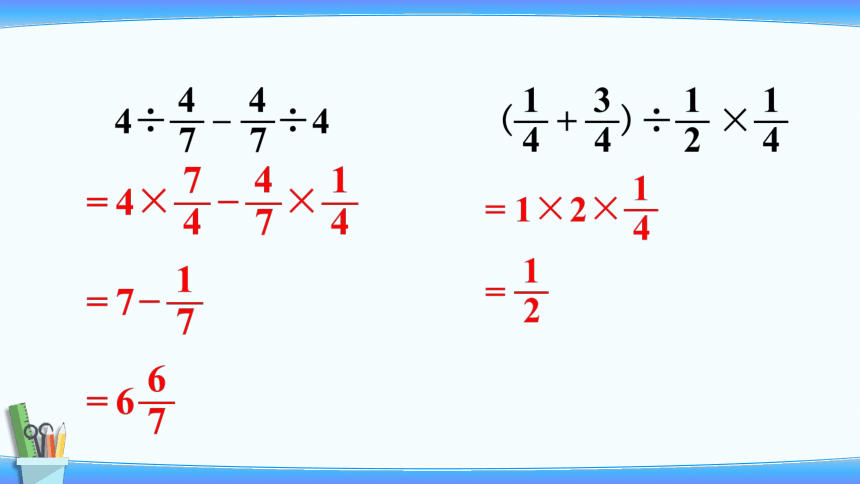




文档简介
(共30张PPT)
圆柱和圆锥
练习三
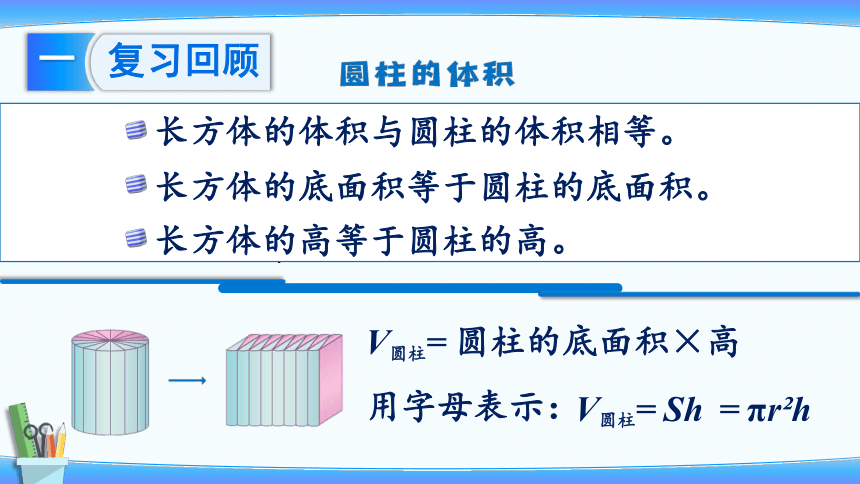
把圆柱的底面积平均分成若干份(平均分的份数越多,拼成的物体就越接近于长方体),然后把圆柱切开,可拼成一个近似的长方体。
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
长方体的高等于圆柱的高。
V圆柱=圆柱的底面积×高
V圆柱=Sh =πr h
用字母表示:
(教科书第17页~19页)
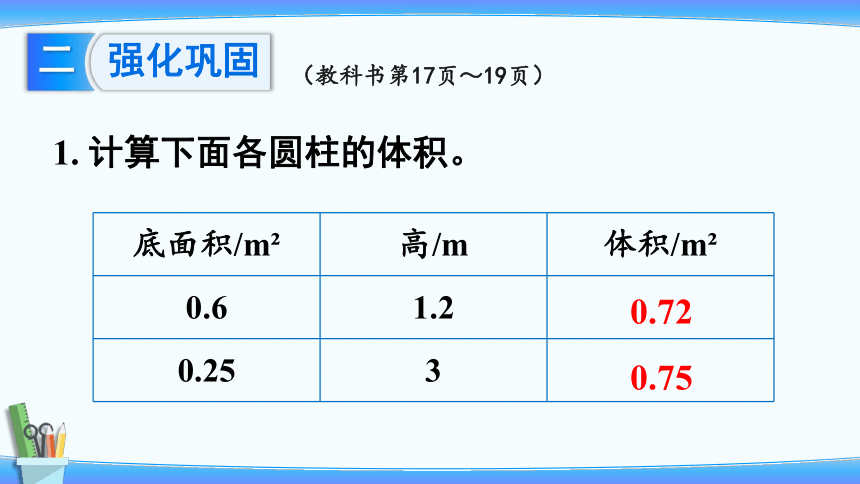
1. 计算下面各圆柱的体积。
底面积/m 高/m 体积/m
0.6 1.2
0.25 3
0.72
0.75
2. 一个圆柱形电饭煲,从里面量,底面直径是3
分米,高是2.4分米。这个电饭煲的容积大约
是多少升?(得数保留一位小数)
(3÷2) ×3.14×2.4≈17.0(升)
答:这个电饭煲的容积大约是17.0升。
3.
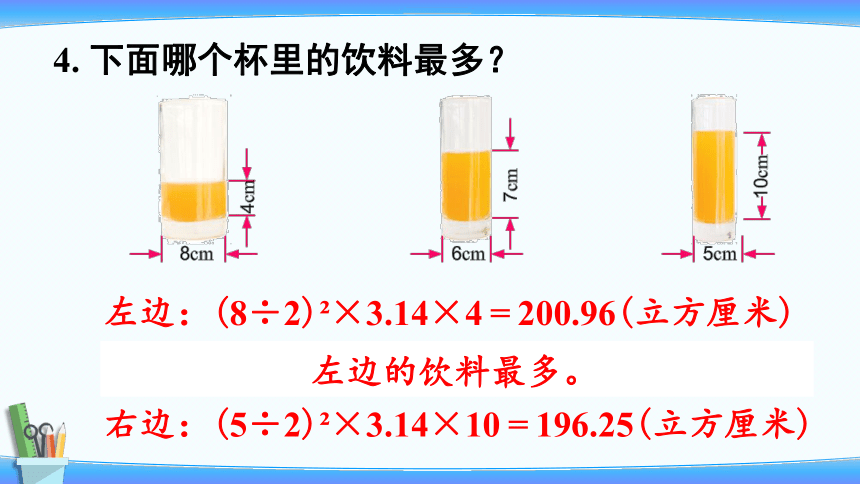
4. 下面哪个杯里的饮料最多?
左边:(8÷2) ×3.14×4=200.96(立方厘米)
中间:(6÷2) ×3.14×7=197.82(立方厘米)
右边:(5÷2) ×3.14×10=196.25(立方厘米)
左边的饮料最多。
5. 一个圆柱形保温茶桶,从里面量,底面半
径是3分米,高是5分米。如果每立方分
米水重1千克,这个保温茶桶能盛150千
克水吗?
3 ×3.14×5×1=141.3(千克)
141.3<150
答:这个保温茶桶不能盛150千克水。
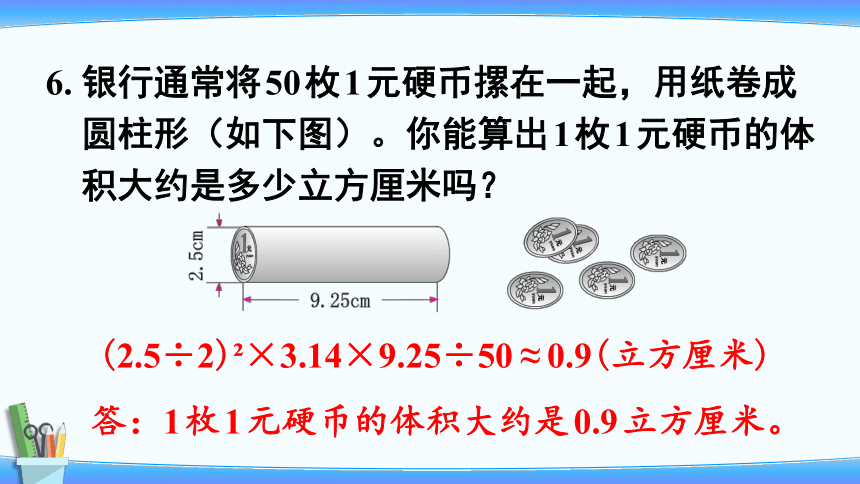
6. 银行通常将50枚1元硬币摞在一起,用纸卷成
圆柱形(如下图)。你能算出1枚1元硬币的体
积大约是多少立方厘米吗?
(2.5÷2) ×3.14×9.25÷50≈0.9(立方厘米)
答:1枚1元硬币的体积大约是0.9立方厘米。
7. 把一张长5厘米、宽4厘米的长方形纸分别绕它
的长和宽旋转一周(如下图),形成两个圆柱。
哪个圆柱的体积大?先估一估,再计算。
绕长旋转:4 ×3.14×5=251.2(立方厘米)
绕宽旋转:5 ×3.14×4=314(立方厘米)
答:绕宽旋转的圆柱的体积大。
8. 一个圆柱形水果罐头,底面周长是25.12厘米,
高是8厘米。这个罐头瓶的容积是多少立方厘
米?(罐头瓶的厚度忽略不计)
(25.12÷3.14÷2) ×3.14×8=401.92(立方厘米)
答:这个罐头瓶的容积是401.92立方厘米。
9. 找一个圆柱形茶杯,从里面量出它的高和底面
直径,算出这个茶杯大约能盛水多少克。(1立
方厘米水重1克)
提示:根据实际情况计算。
10. 计算下面各圆柱的表面积和体积。
圆
柱 底面
半径 底面
直径 底面
周长 高 表面积 体积
5cm 2cm
6dm 10cm
6.28m 5m
10cm
31.4cm
219.8cm
157cm
3dm
18.84dm
244.92dm
282.6dm
1m
2m
37.68m
15.7m
11. 一个圆柱形油桶,从里面量,底面直径是40厘
米,高是50厘米。
(1)它的容积是多少升?
(40÷2) ×3.14×50=62800(立方厘米)
答:它的容积是62.8升。
62800立方厘米=62.8升
(2)如果1升柴油重0.85千克,这个油桶可装柴
油多少千克?
62.8×0.85=53.38(千克)
答:这个油桶可装柴油53.38千克。
(3)做这样一个油桶,至少需要铁皮多少平方分
米?(得数保留一位小数)
40×3.14×50+(40÷2) ×3.14×2
=8792(平方厘米)≈87.9(平方分米)
答:至少需要铁皮87.9平方分米。
12. 一个圆柱形水池,从里面量,底面直径是8米,
深3.5米。
(1)水池里最多能蓄水多少吨?(1立方米水
重1吨)
(8÷2) ×3.14×3.5×1=175.84(吨)
答:水池里最多能蓄水175.84吨。
(2)在水池的底面和四周抹上水泥,抹水泥部分
的面积是多少?
8×3.14×3.5+(8÷2) ×3.14=138.16(平方米)
答:抹水泥部分的面积是138.16平方米。
13. 一个圆柱形蛋糕盒,底面半径是15厘米,高是
20厘米。
(1)做这个蛋糕盒大约要用硬纸板多少平方厘米?
2×15×3.14×20+15 ×3.14×2=3297(平方厘米)
答:做这个蛋糕盒大约要用硬纸板3297平方厘米。
(2)用彩带捆扎这个蛋糕盒(如右图),
至少需要彩带多少厘米?(打结处
大约用彩带15厘米)
15×2×4+20×4+15=215(厘米)
答:至少需要彩带215厘米。
14. 一个用塑料薄膜覆盖的蔬菜大棚,长15米,横
截面是一个半径2米的半圆形。
(1)搭建这个大棚大约要用多
少平方米的塑料薄膜?
2×2×3.14×15÷2+2 ×3.14=106.76(平方米)
答:大约要用106.76平方米的塑料薄膜。
(2)大棚内的空间大约有多大?
2 ×3.14×15÷2=94.2(立方米)
答:大棚内的空间大约有94.2立方米。
15. 玲玲把一块长方体橡皮泥(如右图)
捏成一个高是8厘米的圆柱。捏成的
圆柱的底面积是多少平方厘米?
6×3×4÷8=9(平方厘米)
答:捏成的圆柱的底面积是9平方厘米。
答:水面高1分米。
在一个圆柱形储水桶里,把一段底面半径为5厘米的圆柱形钢材全部放入水中,这是水面上升9厘米。把这段钢材竖着拉出水面8厘米,水面下降4厘米。求这段钢材的体积。
分析:把钢材竖着拉出水面8厘米,拉出的钢材的体积是3.14×5 ×8=628(立方厘米)。拉出的钢材的体积等于水桶中4厘米深的水的体积,从而可以求出水桶的底面积是628÷4=157(平方厘米)。再根据钢材的体积等于水桶中9厘米深的水的体积即可求出钢材的体积。
3.15×5 ×8÷4×9=1413(立方厘米)
答:这段钢材的体积是1413立方厘米。
准备圆柱形容器1个,土豆一个。先在容器内放入适量的水,再把土豆浸没在水中,测量并记录相关数据,算出土豆的体积。
(教科书第19页)
实际操作时要注意什么?与同学交流。
容器的底面积/cm 放入土豆前水面高度/cm 放入土豆前水面高度/cm 土豆的体积/cm
根据圆柱的体积公式可知,要求圆柱的体积,必须知道它的底面积和高。当底面积和高未知时,要先根据已知条件求出来,再来求体积。
等体积变形的实际问题,要“变中找不变”,即变化的只是形状,而不变的是体积。
根据圆柱的体积公式可知,已知底面积、高和体积这三个量中的任意两个量就可以求出第三个量,即V=Sh, S=V÷h, h=V÷S。
所要求的物体的质量等于1个单位体积的质量体积,在计算时要注意单位的统一。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
圆柱和圆锥
练习三
把圆柱的底面积平均分成若干份(平均分的份数越多,拼成的物体就越接近于长方体),然后把圆柱切开,可拼成一个近似的长方体。
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
长方体的高等于圆柱的高。
V圆柱=圆柱的底面积×高
V圆柱=Sh =πr h
用字母表示:
(教科书第17页~19页)
1. 计算下面各圆柱的体积。
底面积/m 高/m 体积/m
0.6 1.2
0.25 3
0.72
0.75
2. 一个圆柱形电饭煲,从里面量,底面直径是3
分米,高是2.4分米。这个电饭煲的容积大约
是多少升?(得数保留一位小数)
(3÷2) ×3.14×2.4≈17.0(升)
答:这个电饭煲的容积大约是17.0升。
3.
4. 下面哪个杯里的饮料最多?
左边:(8÷2) ×3.14×4=200.96(立方厘米)
中间:(6÷2) ×3.14×7=197.82(立方厘米)
右边:(5÷2) ×3.14×10=196.25(立方厘米)
左边的饮料最多。
5. 一个圆柱形保温茶桶,从里面量,底面半
径是3分米,高是5分米。如果每立方分
米水重1千克,这个保温茶桶能盛150千
克水吗?
3 ×3.14×5×1=141.3(千克)
141.3<150
答:这个保温茶桶不能盛150千克水。
6. 银行通常将50枚1元硬币摞在一起,用纸卷成
圆柱形(如下图)。你能算出1枚1元硬币的体
积大约是多少立方厘米吗?
(2.5÷2) ×3.14×9.25÷50≈0.9(立方厘米)
答:1枚1元硬币的体积大约是0.9立方厘米。
7. 把一张长5厘米、宽4厘米的长方形纸分别绕它
的长和宽旋转一周(如下图),形成两个圆柱。
哪个圆柱的体积大?先估一估,再计算。
绕长旋转:4 ×3.14×5=251.2(立方厘米)
绕宽旋转:5 ×3.14×4=314(立方厘米)
答:绕宽旋转的圆柱的体积大。
8. 一个圆柱形水果罐头,底面周长是25.12厘米,
高是8厘米。这个罐头瓶的容积是多少立方厘
米?(罐头瓶的厚度忽略不计)
(25.12÷3.14÷2) ×3.14×8=401.92(立方厘米)
答:这个罐头瓶的容积是401.92立方厘米。
9. 找一个圆柱形茶杯,从里面量出它的高和底面
直径,算出这个茶杯大约能盛水多少克。(1立
方厘米水重1克)
提示:根据实际情况计算。
10. 计算下面各圆柱的表面积和体积。
圆
柱 底面
半径 底面
直径 底面
周长 高 表面积 体积
5cm 2cm
6dm 10cm
6.28m 5m
10cm
31.4cm
219.8cm
157cm
3dm
18.84dm
244.92dm
282.6dm
1m
2m
37.68m
15.7m
11. 一个圆柱形油桶,从里面量,底面直径是40厘
米,高是50厘米。
(1)它的容积是多少升?
(40÷2) ×3.14×50=62800(立方厘米)
答:它的容积是62.8升。
62800立方厘米=62.8升
(2)如果1升柴油重0.85千克,这个油桶可装柴
油多少千克?
62.8×0.85=53.38(千克)
答:这个油桶可装柴油53.38千克。
(3)做这样一个油桶,至少需要铁皮多少平方分
米?(得数保留一位小数)
40×3.14×50+(40÷2) ×3.14×2
=8792(平方厘米)≈87.9(平方分米)
答:至少需要铁皮87.9平方分米。
12. 一个圆柱形水池,从里面量,底面直径是8米,
深3.5米。
(1)水池里最多能蓄水多少吨?(1立方米水
重1吨)
(8÷2) ×3.14×3.5×1=175.84(吨)
答:水池里最多能蓄水175.84吨。
(2)在水池的底面和四周抹上水泥,抹水泥部分
的面积是多少?
8×3.14×3.5+(8÷2) ×3.14=138.16(平方米)
答:抹水泥部分的面积是138.16平方米。
13. 一个圆柱形蛋糕盒,底面半径是15厘米,高是
20厘米。
(1)做这个蛋糕盒大约要用硬纸板多少平方厘米?
2×15×3.14×20+15 ×3.14×2=3297(平方厘米)
答:做这个蛋糕盒大约要用硬纸板3297平方厘米。
(2)用彩带捆扎这个蛋糕盒(如右图),
至少需要彩带多少厘米?(打结处
大约用彩带15厘米)
15×2×4+20×4+15=215(厘米)
答:至少需要彩带215厘米。
14. 一个用塑料薄膜覆盖的蔬菜大棚,长15米,横
截面是一个半径2米的半圆形。
(1)搭建这个大棚大约要用多
少平方米的塑料薄膜?
2×2×3.14×15÷2+2 ×3.14=106.76(平方米)
答:大约要用106.76平方米的塑料薄膜。
(2)大棚内的空间大约有多大?
2 ×3.14×15÷2=94.2(立方米)
答:大棚内的空间大约有94.2立方米。
15. 玲玲把一块长方体橡皮泥(如右图)
捏成一个高是8厘米的圆柱。捏成的
圆柱的底面积是多少平方厘米?
6×3×4÷8=9(平方厘米)
答:捏成的圆柱的底面积是9平方厘米。
答:水面高1分米。
在一个圆柱形储水桶里,把一段底面半径为5厘米的圆柱形钢材全部放入水中,这是水面上升9厘米。把这段钢材竖着拉出水面8厘米,水面下降4厘米。求这段钢材的体积。
分析:把钢材竖着拉出水面8厘米,拉出的钢材的体积是3.14×5 ×8=628(立方厘米)。拉出的钢材的体积等于水桶中4厘米深的水的体积,从而可以求出水桶的底面积是628÷4=157(平方厘米)。再根据钢材的体积等于水桶中9厘米深的水的体积即可求出钢材的体积。
3.15×5 ×8÷4×9=1413(立方厘米)
答:这段钢材的体积是1413立方厘米。
准备圆柱形容器1个,土豆一个。先在容器内放入适量的水,再把土豆浸没在水中,测量并记录相关数据,算出土豆的体积。
(教科书第19页)
实际操作时要注意什么?与同学交流。
容器的底面积/cm 放入土豆前水面高度/cm 放入土豆前水面高度/cm 土豆的体积/cm
根据圆柱的体积公式可知,要求圆柱的体积,必须知道它的底面积和高。当底面积和高未知时,要先根据已知条件求出来,再来求体积。
等体积变形的实际问题,要“变中找不变”,即变化的只是形状,而不变的是体积。
根据圆柱的体积公式可知,已知底面积、高和体积这三个量中的任意两个量就可以求出第三个量,即V=Sh, S=V÷h, h=V÷S。
所要求的物体的质量等于1个单位体积的质量体积,在计算时要注意单位的统一。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
