【双减-同步分层作业】27.1图形的相似(含答案)
文档属性
| 名称 | 【双减-同步分层作业】27.1图形的相似(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 14:02:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【双减—同步分层作业】27.1图形的相似
一、知识梳理
1、已知,则代数式的值是_______。
2、如图所示的两个四边形相似,则的度数是_________。
二、夯实基础(必做题)
1、若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4cm,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
2、下列说法不正确的是( )
A.所有矩形都是相似的
B.若线段a=5cm,b=2cm,则a:b=5:2
C.菱形的对角线互相垂直
D.四条长度依次为1cm,2cm,2cm,4cm的线段是成比例线段
3、如图,矩形相框的外框矩形的长为12dm,宽为8dm,上下边框的宽度都为xcm,左右边框的宽度都为ydm,则符合下列条件的x,y的值能使内边框矩形和外边框矩形相似的为( )
A.x=y B.3x=2y C.x=1,y=2 D.x=3,y=2
(第3题图) (第5题图) (第8题图) (第9题图)
4、若,则=( )
A.-1或 B.-1 C. D.不能确定
5、如图,Rt△ABC与Rt△ADE相似,且∠B=60°,CD=2,DE=1,则BC的长为( )
A.2 B. C. D.
6、已知,且,则的值为________
7、在比例尺为1:50000的地图上量出A、B两地的距离是12cm,则A、B两地的实际距离是________千米。
8、如图,在已建立直角坐标系的4×4正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是 .
9、如图,在长为15 cm,宽为6 cm的矩形ABCD中,截去一个矩形ABFE,使得留下的矩形EFCD与截去的矩形ABFE相似(全等除外),则所截取的线段AE的长度可以是 .
10、已知两个相似的四边形如图所示,根据已知数据,求x,y,α.
11、顺次连接正方形各边的中点得到的图形与原来的正方形是否相似 若相似,它们的相似比是多少
12、已知。求和的值。
13、有16 K和32 K两种纸,把它们纵向放置时,它们的宽度和高度的比可近似地看作相同,其中32 K纸的宽度为130 mm,高度为184 mm;16 K纸的宽度为184 mm,求16 K纸的高度约为多少毫米 (精确到1 mm)
三、能力提升(中等生加练题)
1、生活中到处可见黄金分割的美.如图,在设计人体雕像时,
使雕像的腰部以下a与全身b的高度比值接近0.618,可以
增加视觉美感.若图中b为2米,则a约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
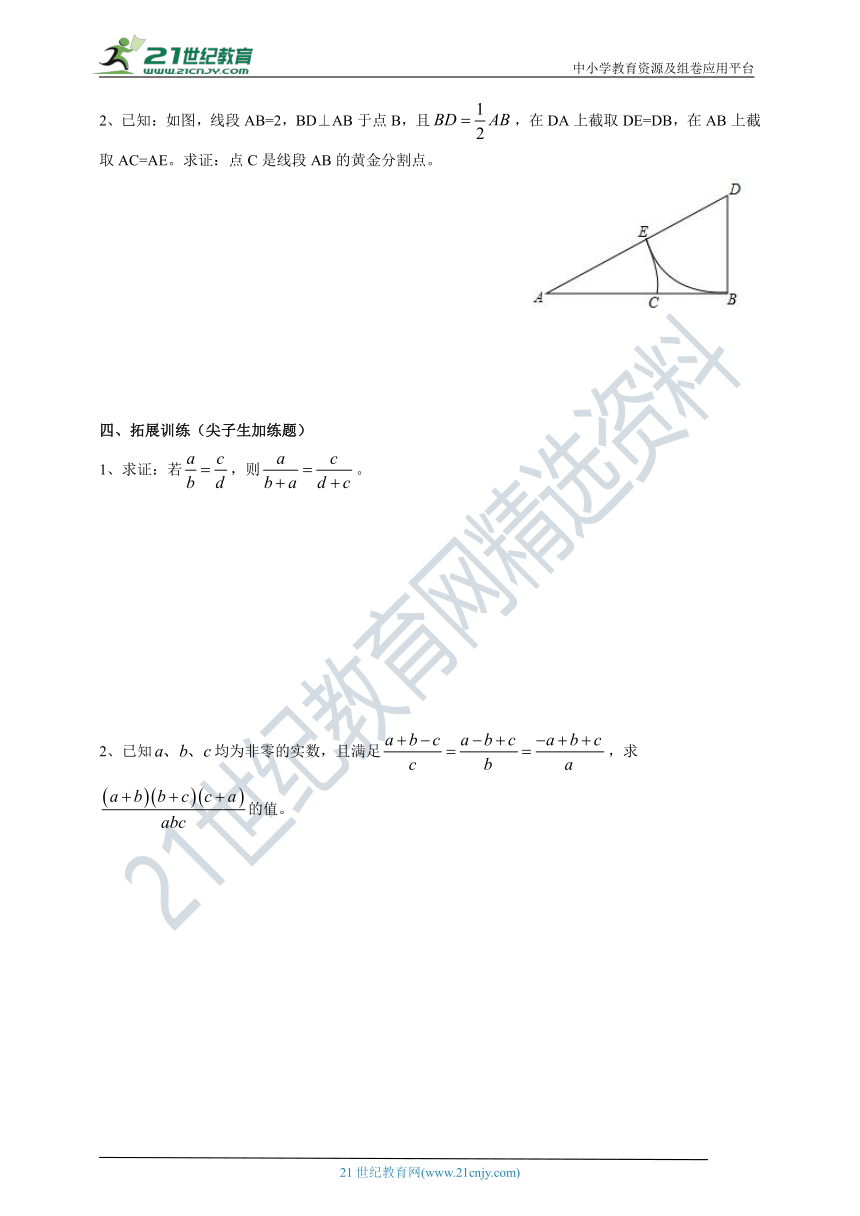
2、已知:如图,线段AB=2,BD⊥AB于点B,且,在DA上截取DE=DB,在AB上截取AC=AE。求证:点C是线段AB的黄金分割点。
四、拓展训练(尖子生加练题)
1、求证:若,则。
2、已知均为非零的实数,且满足,求
的值。
【参考答案】
一、
1、
2、87°
二、
1、B
2、A
3、B
【解析】依题意得
即
∴
∴
4、A
【解析】当时,
当时,,所以选A。
5、B
6、4
7、6
8、(1,4)或(3,4)或(3,1)
9、12cm或3cm
【解析】设AE=xcm,则ED=(15-x)cm,依题意得
,即,解得
10、解:依题意得,
即,,解得
依题意得
∴
11、解:得到的正方形与原来的正方形相似。相似比为。理由如下:
设原来的正方形的边长AB为,则AH=AE=
在Rt△AEH中,
∴
∴得到的正方形与原来的正方形相似,相似比为。
12、解: ∵
∴
∴ ,
13、解:设16K纸的高度为x毫米,依题意得
解得
答:16K纸的高度约为260毫米。
三、
1、A
【解析】依题意得,则,解得
2、证明:∵AB=2,
∴
∵BD⊥AB
∴在Rt△ABD中,
∵DE=DB
∴DE=DB=1
∴
∵AC=AE
∴AC=AE=
∴
∴点C是线段AB的黄金分割点。
四、
1、证明:∵
∴
∴
即
∴
2、解:当时,
=
∴
∴
∴原式=
当时,
原式=
∴原式的值为8或-1。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【双减—同步分层作业】27.1图形的相似
一、知识梳理
1、已知,则代数式的值是_______。
2、如图所示的两个四边形相似,则的度数是_________。
二、夯实基础(必做题)
1、若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4cm,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
2、下列说法不正确的是( )
A.所有矩形都是相似的
B.若线段a=5cm,b=2cm,则a:b=5:2
C.菱形的对角线互相垂直
D.四条长度依次为1cm,2cm,2cm,4cm的线段是成比例线段
3、如图,矩形相框的外框矩形的长为12dm,宽为8dm,上下边框的宽度都为xcm,左右边框的宽度都为ydm,则符合下列条件的x,y的值能使内边框矩形和外边框矩形相似的为( )
A.x=y B.3x=2y C.x=1,y=2 D.x=3,y=2
(第3题图) (第5题图) (第8题图) (第9题图)
4、若,则=( )
A.-1或 B.-1 C. D.不能确定
5、如图,Rt△ABC与Rt△ADE相似,且∠B=60°,CD=2,DE=1,则BC的长为( )
A.2 B. C. D.
6、已知,且,则的值为________
7、在比例尺为1:50000的地图上量出A、B两地的距离是12cm,则A、B两地的实际距离是________千米。
8、如图,在已建立直角坐标系的4×4正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是 .
9、如图,在长为15 cm,宽为6 cm的矩形ABCD中,截去一个矩形ABFE,使得留下的矩形EFCD与截去的矩形ABFE相似(全等除外),则所截取的线段AE的长度可以是 .
10、已知两个相似的四边形如图所示,根据已知数据,求x,y,α.
11、顺次连接正方形各边的中点得到的图形与原来的正方形是否相似 若相似,它们的相似比是多少
12、已知。求和的值。
13、有16 K和32 K两种纸,把它们纵向放置时,它们的宽度和高度的比可近似地看作相同,其中32 K纸的宽度为130 mm,高度为184 mm;16 K纸的宽度为184 mm,求16 K纸的高度约为多少毫米 (精确到1 mm)
三、能力提升(中等生加练题)
1、生活中到处可见黄金分割的美.如图,在设计人体雕像时,
使雕像的腰部以下a与全身b的高度比值接近0.618,可以
增加视觉美感.若图中b为2米,则a约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
2、已知:如图,线段AB=2,BD⊥AB于点B,且,在DA上截取DE=DB,在AB上截取AC=AE。求证:点C是线段AB的黄金分割点。
四、拓展训练(尖子生加练题)
1、求证:若,则。
2、已知均为非零的实数,且满足,求
的值。
【参考答案】
一、
1、
2、87°
二、
1、B
2、A
3、B
【解析】依题意得
即
∴
∴
4、A
【解析】当时,
当时,,所以选A。
5、B
6、4
7、6
8、(1,4)或(3,4)或(3,1)
9、12cm或3cm
【解析】设AE=xcm,则ED=(15-x)cm,依题意得
,即,解得
10、解:依题意得,
即,,解得
依题意得
∴
11、解:得到的正方形与原来的正方形相似。相似比为。理由如下:
设原来的正方形的边长AB为,则AH=AE=
在Rt△AEH中,
∴
∴得到的正方形与原来的正方形相似,相似比为。
12、解: ∵
∴
∴ ,
13、解:设16K纸的高度为x毫米,依题意得
解得
答:16K纸的高度约为260毫米。
三、
1、A
【解析】依题意得,则,解得
2、证明:∵AB=2,
∴
∵BD⊥AB
∴在Rt△ABD中,
∵DE=DB
∴DE=DB=1
∴
∵AC=AE
∴AC=AE=
∴
∴点C是线段AB的黄金分割点。
四、
1、证明:∵
∴
∴
即
∴
2、解:当时,
=
∴
∴
∴原式=
当时,
原式=
∴原式的值为8或-1。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
