小学数学苏教版六年级下3.2 解决问题的策略 课件(共17张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下3.2 解决问题的策略 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 06:30:33 | ||
图片预览






文档简介
(共17张PPT)
解决问题的策略
第2课时 解决问题的策略(2)
把分数转化成比,更容易理解数量之间的关系。
提示:椅子:桌子=1:3
90元
30元
全班42人去公园划船,租10只船正好坐满。每
只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
2
(教科书第28页例2)
已知:
共42人
大船可坐5人
小船可坐3人
10只船正好坐满42人
分析数量关系
根据条件选择合适的策略
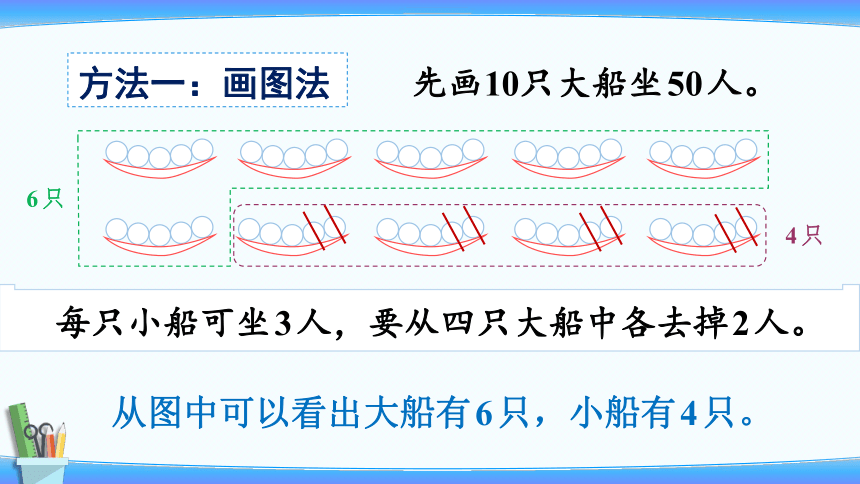
先画10只大船坐50人。
方法一:画图法
从图中可以看出大船有6只,小船有4只。
每只小船可坐3人,要从四只大船中各去掉2人。
6只
4只
方法二:列表法
①从大船有9只,小船有1只开始列举,一直到
找到符合要求的答案为止。
大船只数 小船只数 乘坐的总人数 和42人比较
9 1
9×5+3=48
多了6人
8
2
8×5+2×3=46
多了4人
7
3
7×5+3×3=44
多了2人
6
4
6×5+4×3=42
正好
②从大船和小船同样多开始列举,再根据总人
数进行调整。
大船只数 小船只数 乘坐的总人数 和42人比较
5 5
9×5+3=48
少了2人
6
4
6×5+4×3=46
正好
方法三:假设法
假设全部是大船。
小船的只数是8÷2=4(只)
大船的只数是10 2=6(只)
10只大船可乘坐50人,比42人还多8人;
因为每只小船比每只大船少坐2人,所以小船
的只数是8÷2=4(只),大船的只数是10 4=
6(只)。
小船:(10×5 42)÷(5 3)=4(只)
大船: 10 4=6(只)
列式
方法三:假设法
假设全部是小船。
小船的只数是8÷2=4(只)
大船的只数是10 2=6(只)
10只小船可乘坐30人,实际上有42人;
多了12人是因为把大船当做了小船;
大船:(42 10×3)÷(5 3)=6(只)
小船: 10 6=4(只)
列式
每只大船比小船多坐了2人,也就是说12÷2
=6(只) ,则小船有4只。
方法四:列方程
设大船有x只,则小船有(10 x)只;
列式
5x+3(10 x)=42
2x=12
x=6
10 x=10 6=4
根据大船坐的总人数+小船坐的总人数=全班人数,列方程解答。
答:租的大船有6只,
小船有4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
小船:(10×5 42)÷(5 3)=4(只)
大船: 10 4=6(只)
检验:
解答正确。
5×6+3×4=42(人)
6+4=10(只)
(教科书第29页练一练)
(1)按照下面的步骤画图。
①画8个圆,表示一共有8只动物。
②假设8只都是鸡,给每只动物画2条腿。
算一算画出的腿比22条少多少条。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?(根据下面的提示,选择一种方法找出答案)
③一只兔比一只鸡多2条腿,给其中的几只动物
填上2条腿,是画出的腿正好是22条。
④鸡有( )只,兔有( )只。
8只动物
若都是鸡
16条腿,少6条
5
3
兔
鸡
(2)先假设鸡和兔同样多,再调整。
鸡的只数 兔的只数 腿的总条数 和22条比较
4 4 4×2+4×4=24
5
3
5×2+3×4=24
多2条
相等
1. 停车场有小轿车和摩托车共36辆,这些车共有
100个车轮,小轿车和摩托车各有多少辆?
小轿车:(100 36×2)÷(4 2)=14(辆)
摩托车: 36 14=22(辆)
答:小轿车有14辆,摩托车有22辆。
2. 鸡与兔共有120只,鸡的脚数比兔的脚数多60
只,鸡、兔各有多少只?
60÷4=15(只)
120+15=135(只)
鸡的只数:兔的只数=2:1
兔:120 90=30(只)
答:鸡有90只,兔有30只。
提示:假设再增加15只兔,则鸡、兔的脚数一样多,那么鸡的只数就应该是兔的2倍。
画图、列表是把一个数学问题具体形象化,从而把复杂的问题简单化,并使问题得以解决的有效策略。
用画图、列表的策略解决问题
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
解决问题的策略
第2课时 解决问题的策略(2)
把分数转化成比,更容易理解数量之间的关系。
提示:椅子:桌子=1:3
90元
30元
全班42人去公园划船,租10只船正好坐满。每
只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
2
(教科书第28页例2)
已知:
共42人
大船可坐5人
小船可坐3人
10只船正好坐满42人
分析数量关系
根据条件选择合适的策略
先画10只大船坐50人。
方法一:画图法
从图中可以看出大船有6只,小船有4只。
每只小船可坐3人,要从四只大船中各去掉2人。
6只
4只
方法二:列表法
①从大船有9只,小船有1只开始列举,一直到
找到符合要求的答案为止。
大船只数 小船只数 乘坐的总人数 和42人比较
9 1
9×5+3=48
多了6人
8
2
8×5+2×3=46
多了4人
7
3
7×5+3×3=44
多了2人
6
4
6×5+4×3=42
正好
②从大船和小船同样多开始列举,再根据总人
数进行调整。
大船只数 小船只数 乘坐的总人数 和42人比较
5 5
9×5+3=48
少了2人
6
4
6×5+4×3=46
正好
方法三:假设法
假设全部是大船。
小船的只数是8÷2=4(只)
大船的只数是10 2=6(只)
10只大船可乘坐50人,比42人还多8人;
因为每只小船比每只大船少坐2人,所以小船
的只数是8÷2=4(只),大船的只数是10 4=
6(只)。
小船:(10×5 42)÷(5 3)=4(只)
大船: 10 4=6(只)
列式
方法三:假设法
假设全部是小船。
小船的只数是8÷2=4(只)
大船的只数是10 2=6(只)
10只小船可乘坐30人,实际上有42人;
多了12人是因为把大船当做了小船;
大船:(42 10×3)÷(5 3)=6(只)
小船: 10 6=4(只)
列式
每只大船比小船多坐了2人,也就是说12÷2
=6(只) ,则小船有4只。
方法四:列方程
设大船有x只,则小船有(10 x)只;
列式
5x+3(10 x)=42
2x=12
x=6
10 x=10 6=4
根据大船坐的总人数+小船坐的总人数=全班人数,列方程解答。
答:租的大船有6只,
小船有4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
小船:(10×5 42)÷(5 3)=4(只)
大船: 10 4=6(只)
检验:
解答正确。
5×6+3×4=42(人)
6+4=10(只)
(教科书第29页练一练)
(1)按照下面的步骤画图。
①画8个圆,表示一共有8只动物。
②假设8只都是鸡,给每只动物画2条腿。
算一算画出的腿比22条少多少条。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?(根据下面的提示,选择一种方法找出答案)
③一只兔比一只鸡多2条腿,给其中的几只动物
填上2条腿,是画出的腿正好是22条。
④鸡有( )只,兔有( )只。
8只动物
若都是鸡
16条腿,少6条
5
3
兔
鸡
(2)先假设鸡和兔同样多,再调整。
鸡的只数 兔的只数 腿的总条数 和22条比较
4 4 4×2+4×4=24
5
3
5×2+3×4=24
多2条
相等
1. 停车场有小轿车和摩托车共36辆,这些车共有
100个车轮,小轿车和摩托车各有多少辆?
小轿车:(100 36×2)÷(4 2)=14(辆)
摩托车: 36 14=22(辆)
答:小轿车有14辆,摩托车有22辆。
2. 鸡与兔共有120只,鸡的脚数比兔的脚数多60
只,鸡、兔各有多少只?
60÷4=15(只)
120+15=135(只)
鸡的只数:兔的只数=2:1
兔:120 90=30(只)
答:鸡有90只,兔有30只。
提示:假设再增加15只兔,则鸡、兔的脚数一样多,那么鸡的只数就应该是兔的2倍。
画图、列表是把一个数学问题具体形象化,从而把复杂的问题简单化,并使问题得以解决的有效策略。
用画图、列表的策略解决问题
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
