小学数学苏教版六年级下三 解决问题的策略 练习五 课件(共21张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下三 解决问题的策略 练习五 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
解决问题的策略
练习五
用转化的策略解决问题
转化是把一个数学问题转变为一类已经解决或比较容易解决的问题,从而使原问题得以解决的一种策略。转化的关键是要根据具体的问题,确定转化后要实现的目标和具体的转化方法。
画图、列表是把一个数学问题具体形象化,从而把复杂的问题简单化,并使问题得以解决的有效策略。
用画图、列表的策略解决问题
分析和解决同一个问题,可以用不同的策略,应根据具体问题灵活选择策略。
(教科书第30页~32页)
1. 看图填空。
2
5
3
5
和剩下的
果汁的比是( ):( )。
2
3
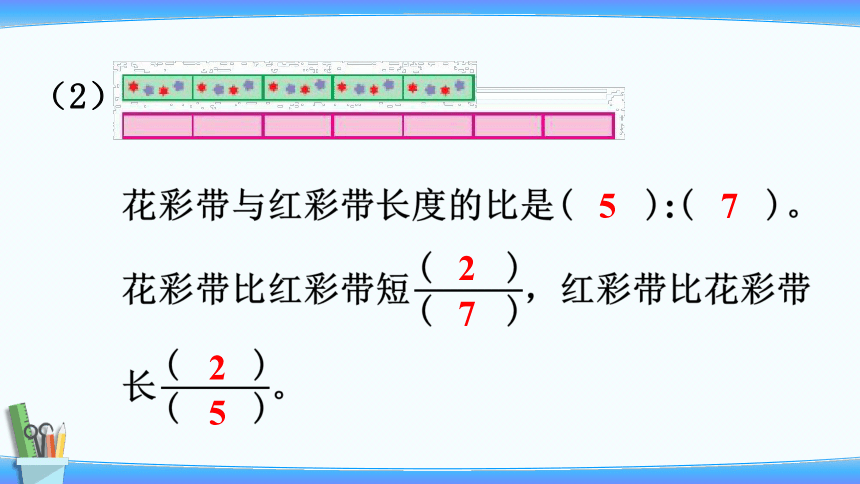
(2)
5
7
2
7
2
5
2. 先根据题意把线段图补充完整,再解答。
(1)一辆汽车从甲地开往乙地,已经行驶了全
程的30%,离乙地还有140千米。这辆汽
车行驶了多少千米?
甲地
乙地
30%
140千米
甲、乙两地全程:140÷70%=200(千米)
已行驶距离:200×30%=60(千米)
答:这辆汽车行驶了60千米。
(2)六年级生物小组养的白兔和黑兔只数的比是
5:3,白兔比黑兔多12只。白兔和黑兔一共
有多少只?
白兔
黑兔
12只
?只
?只
白兔:12÷(5 3)×5=30(只)
黑兔:30 12=18(只)
兔子总数:30+18=48(只)
答:白兔和黑兔一共有48只。
你知道男、女运动员各有多少人吗?
答:男运动员有75
人,女运动
员有100人。
4. 六年级同学制作了78件蝴蝶标本,贴在9块展
板上展出。每块小展板贴6件,每块大展板贴
10件。两种展板各有多少块?
大展板块数 小展板块数 蝴蝶标本总件数 和78件比较
5 4 5×10+4×6=74 少了4件
假设两种展板的块数如下表,你能通过调整得出结果吗?
6
3
6×10+3×6=78
相等
5.
1元的枚数 5角的枚数 总元数 和10元比较
1 12 1+12×0.5=7 少了3元
3
10
3×1+10×0.5=8
少了2元
5
8
5×1+8×0.5=9
少了1元
7
6
7×1+6×0.5=10
相等
根据表中数据,接着想一想、填一填,并找出答案。
6. 小明的书橱一共有三层,上、中、下层书的本
数比是5:6:4。已知上层放了100本书,求中、
下层各放了多少本书。(先画图表示题意,再
解答)
上层:
中层:
下层:
100本
?本
?本
中层:100÷5×6=120(本)
答:中层放了120本,下层放了80本。
下层:100÷5×4=80(本)
甲
乙
客车
货车
相遇
甲
乙
客车
货车
相遇
答:相遇时客车行驶了180千米,货车行
驶了120千米。
货车:300 180=120(千米)
黑子
白子
第一堆
第二堆
第三堆
白子
黑子
黑子
白子
答:这三堆棋子中一共有80枚白子。
黑子
白子
第一堆
第二堆
第三堆
白子
黑子
黑子
白子
9. 一名篮球运动员在一场比赛中一共投中9个球,
有2分球,也有3分球。已知这名运动员一共得
了21分,他投中2分球和3分球各有多少个?
先假设两种球分别投中的个数,再通过实验调整找出答案。
2分球个数 3分球个数 总得分 和21分比较
5
4
5×2+4×3=22
多1分
6
3
6×2+3×3=21
相等
在12张球桌上同时进行乒乓球比赛,双打的比单打的多6人。进行单打和双打比赛的乒乓球桌各有几张?
分析:用列表的方法,即先假设进行单打和双打比赛的乒乓球桌同样多,再作调整。
单打的桌数 双打的桌数 双打人数同单打人数相比
答:进行单打和双打比赛的乒乓球桌分别有
7张、5张。
6
6
多12人
7
5
多6人
“鸡兔同笼”问题是我国古代的数学名题之一。它出自唐代的《孙子算经》。书中的题目是这样的:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
你能算出这道题中的鸡和兔各有多少只吗?
(教科书第32页)
有些题目的过程比较复杂(或比较抽象),不易于理解,可以采用画图的方法使其变得更直观、形象。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
解决问题的策略
练习五
用转化的策略解决问题
转化是把一个数学问题转变为一类已经解决或比较容易解决的问题,从而使原问题得以解决的一种策略。转化的关键是要根据具体的问题,确定转化后要实现的目标和具体的转化方法。
画图、列表是把一个数学问题具体形象化,从而把复杂的问题简单化,并使问题得以解决的有效策略。
用画图、列表的策略解决问题
分析和解决同一个问题,可以用不同的策略,应根据具体问题灵活选择策略。
(教科书第30页~32页)
1. 看图填空。
2
5
3
5
和剩下的
果汁的比是( ):( )。
2
3
(2)
5
7
2
7
2
5
2. 先根据题意把线段图补充完整,再解答。
(1)一辆汽车从甲地开往乙地,已经行驶了全
程的30%,离乙地还有140千米。这辆汽
车行驶了多少千米?
甲地
乙地
30%
140千米
甲、乙两地全程:140÷70%=200(千米)
已行驶距离:200×30%=60(千米)
答:这辆汽车行驶了60千米。
(2)六年级生物小组养的白兔和黑兔只数的比是
5:3,白兔比黑兔多12只。白兔和黑兔一共
有多少只?
白兔
黑兔
12只
?只
?只
白兔:12÷(5 3)×5=30(只)
黑兔:30 12=18(只)
兔子总数:30+18=48(只)
答:白兔和黑兔一共有48只。
你知道男、女运动员各有多少人吗?
答:男运动员有75
人,女运动
员有100人。
4. 六年级同学制作了78件蝴蝶标本,贴在9块展
板上展出。每块小展板贴6件,每块大展板贴
10件。两种展板各有多少块?
大展板块数 小展板块数 蝴蝶标本总件数 和78件比较
5 4 5×10+4×6=74 少了4件
假设两种展板的块数如下表,你能通过调整得出结果吗?
6
3
6×10+3×6=78
相等
5.
1元的枚数 5角的枚数 总元数 和10元比较
1 12 1+12×0.5=7 少了3元
3
10
3×1+10×0.5=8
少了2元
5
8
5×1+8×0.5=9
少了1元
7
6
7×1+6×0.5=10
相等
根据表中数据,接着想一想、填一填,并找出答案。
6. 小明的书橱一共有三层,上、中、下层书的本
数比是5:6:4。已知上层放了100本书,求中、
下层各放了多少本书。(先画图表示题意,再
解答)
上层:
中层:
下层:
100本
?本
?本
中层:100÷5×6=120(本)
答:中层放了120本,下层放了80本。
下层:100÷5×4=80(本)
甲
乙
客车
货车
相遇
甲
乙
客车
货车
相遇
答:相遇时客车行驶了180千米,货车行
驶了120千米。
货车:300 180=120(千米)
黑子
白子
第一堆
第二堆
第三堆
白子
黑子
黑子
白子
答:这三堆棋子中一共有80枚白子。
黑子
白子
第一堆
第二堆
第三堆
白子
黑子
黑子
白子
9. 一名篮球运动员在一场比赛中一共投中9个球,
有2分球,也有3分球。已知这名运动员一共得
了21分,他投中2分球和3分球各有多少个?
先假设两种球分别投中的个数,再通过实验调整找出答案。
2分球个数 3分球个数 总得分 和21分比较
5
4
5×2+4×3=22
多1分
6
3
6×2+3×3=21
相等
在12张球桌上同时进行乒乓球比赛,双打的比单打的多6人。进行单打和双打比赛的乒乓球桌各有几张?
分析:用列表的方法,即先假设进行单打和双打比赛的乒乓球桌同样多,再作调整。
单打的桌数 双打的桌数 双打人数同单打人数相比
答:进行单打和双打比赛的乒乓球桌分别有
7张、5张。
6
6
多12人
7
5
多6人
“鸡兔同笼”问题是我国古代的数学名题之一。它出自唐代的《孙子算经》。书中的题目是这样的:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
你能算出这道题中的鸡和兔各有多少只吗?
(教科书第32页)
有些题目的过程比较复杂(或比较抽象),不易于理解,可以采用画图的方法使其变得更直观、形象。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
