5.3 密度知识的应用 课件 2021-22学年沪粤版八年级物理上册(共30张PPT)
文档属性
| 名称 | 5.3 密度知识的应用 课件 2021-22学年沪粤版八年级物理上册(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
温故知新
1、密度的定义:
2、密度的公式:
把某种物质的质量与体积的比值,叫做这种物质的密度。
(比值法)
密度
质量
体积
=
3、密度的单位:
ρ =
m
V
kg/m3
国际单位:
常用单位:
g/cm3
1g/cm3=
kg/m3
103
4、密度的物理意义:
例:ρ铜=8.9x103kg/m3的物理意义是
体积为1m3的铜质量是8.9x103kg
1kg/dm3=
kg/m3
=
g/cm3
103
1
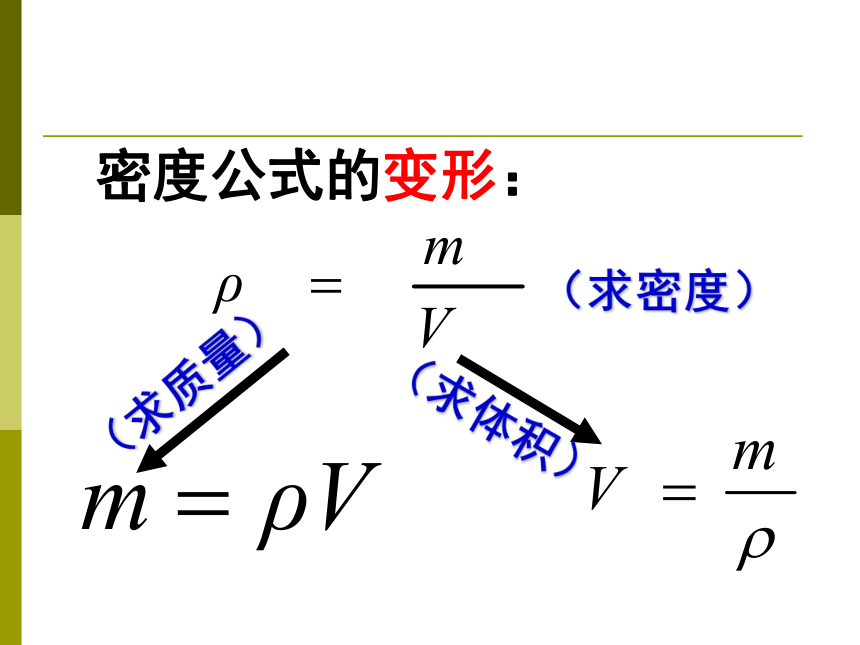
密度公式的变形:
(求密度)
(求质量)
(求体积)
5.3 密度知识的应用
常见物质的密度(见课本P120)
1:铜的密度是_____________
铁的密度是_____________
铝的密度是_____________
冰的密度是_____________
8.9×103kg/m3
7.9×103kg/m3
2.7×103kg/m3
0.9×103kg/m3
查表:填写以下几种常见物质的密度
固体
或8.9g/cm3
2:水银的密度是___________
海水的密度是___________
纯水的密度是___________
煤油的密度是___________
酒精的密度是___________
13.6×103kg/m3
1.03×103kg/m3
1.0×103kg/m3
0.8×103kg/m3
0.8×103kg/m3
(记住)
常见物质的密度(见课本P120)
查表:填写以下几种常见物质的密度
液体
密度相同
3:空气的密度是___________
1.29 kg/m3
常见物质的密度(见课本P121)
查表:填写以下几种常见物质的密度
气体
1、不同物质密度一般不同
2、固体的密度较大,气体的密度较小
3、同种物质状态不同,密度不同
分析:
一、简单计算
1、求密度(鉴别物质):
ρ=m/v
2、求质量:
m=ρ v
3、求体积:
v=m/ρ
例1:一卷细铜丝质量为890g,求其体积。
m铜=890g
ρ铜=8.9x103kg/m3
V铜
=
答:
细铜丝的体积为100cm3
解:
已知:
求:
理解密度公式ρ=m/v
例1:一杯水倒掉一半,它的密度变化吗?为什么?
不变
同种物质的密度是相同的,与其质量与体积无关。
物质的密度与种类、状态有关。
与其质量与体积无关。
记住:
理解密度公式ρ=m/v
例2:一钢块切掉一半后,它的质量、体积和密度有变化吗?
质量减小、体积减小,但是密度不变。
特殊:(气体)
一瓶氧气用去一半,它的质量、体积和密度有变化吗?
质量减小、体积不变,密度减小。
二、不变问题
质量不变问题
(如:水结成冰,冰化成水)
体积不变问题
(如:瓶子或容器问题)
密度不变问题
(如:样品问题)
例:求1 m3的冰熔化成水后的体积
思路:冰熔化成水的过程中,质量不变
答:
解:
已知:
求:
V冰=1m3
ρ冰=0.9x103kg/m3
ρ水=1.0x103kg/m3
V水
例:一个瓶子能盛满1kg水,用这个瓶子装满0.8kg某液体,该液体可能是什么?
思路:用同一瓶子两次装满液体的过程中,两种液体的体积相等且等于瓶子的容积。
例:从体积为100cm3质量为300g的物质中取出90g做成零件,求此零件的体积
思路:在从物质中提取部分做零件的过程中,物质的密度不变。
三、空心问题
1、判断空心实心
2、计算空心部分的体积
例:一个铜球的质量是178g,体积为50cm3,这个球是空心的还是实心的?
思路:
解决这类题目的关键就是建立假设条件,可以假定它是实心的,然后从比较密度、质量、体积三个方面考虑
比较密度 比较质量 比较体积
若在上述题目的基础上继续问,若为空心,请计算出空心部分的体积。则如何计算?
上述计算已经计算出178g的铜所占的体积,现在的铜球的体积已知为50cm3,则空心部分的体积即为两者之差。
空心部分 V=V球-V实=50-20=30(cm3)
四、比例计算问题
例:甲乙两物体的体积之比为2:3,质量之比为8:9,求它们的密度之比。
练习1:
甲乙两物体的密度之比为2:3,质量之比为8:9,求它们的体积之比。
练习2:
甲乙两物体的体积之比为2:3,密度之比为8:9,求它们的质量之比。
小明看到煤气公司价格牌上标有“冬季55元/瓶,夏季51元/瓶”的字样。他寻思着,为什么夏季价格低 他查找了煤气资料:煤气冬季密度为0.88×103kg/m3,夏季为0.8×103kg/m3,煤气瓶容积为0.015m3。通过计算发现夏季价格比冬季价格 (高/低)。若夏季价格和冬季一样,夏季应标价为 元/瓶。
五、煤气价格问题:
现在节水型洁具逐渐进入百姓家庭。所谓节水型洁具,是指每冲一次的耗水量在6L以内的洁具。某家庭新安装一耗水量为5L的节水型洁具,而原有的洁具每次耗水为9L。
①1000kg水可供这节水型洁具冲洗多少次?
②该家庭每月节约用水多少kg?(设平均每天用10次,每月按30天计算)
六、耗水量问题:
用盐水选种,要求密度为1.1×103kg/m3盐水,现有体积为20dm3的盐水,称质量23kg,
(1)这样的盐水是否符合要求?
(2)如不符合要求,应该加盐还是加水?
(3)加多少kg
七、盐水问题:
八、含沙量问题:
为测定黄河水的含沙量
是多少,某同
学取了
10dm
3
的黄河水,称得其质量为
10.18kg
,试求黄河水中的含
沙量。
(
ρ
沙
=
2.5
×
10
3
kg/m
3
)
为测定黄河水的含沙量(每立方米含沙多少千克)是多少,某同学取了10dm3的黄河水,称得其质量为10.18kg,试求黄河水中的含沙量。(ρ沙=2.5×103kg/m3)
九、实验:测固体和液体的密度
实验原理:
实验器材:
ρ=
m
V
托盘天平、量筒、烧杯、水、待测物体
实验一、如何测固体(如小石块)的密度
1.用调好的天平测出石块的质量m
2.在量筒内倒入适量的水,测出水的体积V1
3.将石块放入量筒中,测出总体积V2
实验步骤:
4.石块的密度:
V1
V2
实验二、如何测液体(如酒精)的密度
1.用调好的天平测出烧杯和酒精的总质量m1
2.将部分酒精倒入量筒,测出酒精的体积V
3.用天平测出烧杯和剩余酒精的质量m2
实验步骤:
4.酒精的密度:
V
m1-
V
m
=
r
m2
=
m1
m2
★关于密度的特殊测量★
例:现有天平、烧杯、水、未知名液体,如何利用这些仪器测出该液体的密度。
解:①用天平测出空烧杯质量,记为m1。
②在烧杯里倒入水,并作标记,测出质量记为m2,则m水= m2-m1。
③将水倒出,在烧杯里倒入待测液体至标记处,测质量记为m3,则m液= m3-m1。
④
500g冰熔化成水,体积是多少?
一只空瓶子,它的质量是150g,用它装满水,瓶和水的总质量为350g,换它装煤油可装多少?
不用天平只用量筒,能否测出100g的酒精?
一个木球体积为300cm3,质量为100g,它是实心还是空心?(三种解法)
体积是30cm3的空心铜球质量是89g,将它的中心部分注满某种液体后的球的总质量是361g,问注入的液体是什么物质?
温故知新
1、密度的定义:
2、密度的公式:
把某种物质的质量与体积的比值,叫做这种物质的密度。
(比值法)
密度
质量
体积
=
3、密度的单位:
ρ =
m
V
kg/m3
国际单位:
常用单位:
g/cm3
1g/cm3=
kg/m3
103
4、密度的物理意义:
例:ρ铜=8.9x103kg/m3的物理意义是
体积为1m3的铜质量是8.9x103kg
1kg/dm3=
kg/m3
=
g/cm3
103
1
密度公式的变形:
(求密度)
(求质量)
(求体积)
5.3 密度知识的应用
常见物质的密度(见课本P120)
1:铜的密度是_____________
铁的密度是_____________
铝的密度是_____________
冰的密度是_____________
8.9×103kg/m3
7.9×103kg/m3
2.7×103kg/m3
0.9×103kg/m3
查表:填写以下几种常见物质的密度
固体
或8.9g/cm3
2:水银的密度是___________
海水的密度是___________
纯水的密度是___________
煤油的密度是___________
酒精的密度是___________
13.6×103kg/m3
1.03×103kg/m3
1.0×103kg/m3
0.8×103kg/m3
0.8×103kg/m3
(记住)
常见物质的密度(见课本P120)
查表:填写以下几种常见物质的密度
液体
密度相同
3:空气的密度是___________
1.29 kg/m3
常见物质的密度(见课本P121)
查表:填写以下几种常见物质的密度
气体
1、不同物质密度一般不同
2、固体的密度较大,气体的密度较小
3、同种物质状态不同,密度不同
分析:
一、简单计算
1、求密度(鉴别物质):
ρ=m/v
2、求质量:
m=ρ v
3、求体积:
v=m/ρ
例1:一卷细铜丝质量为890g,求其体积。
m铜=890g
ρ铜=8.9x103kg/m3
V铜
=
答:
细铜丝的体积为100cm3
解:
已知:
求:
理解密度公式ρ=m/v
例1:一杯水倒掉一半,它的密度变化吗?为什么?
不变
同种物质的密度是相同的,与其质量与体积无关。
物质的密度与种类、状态有关。
与其质量与体积无关。
记住:
理解密度公式ρ=m/v
例2:一钢块切掉一半后,它的质量、体积和密度有变化吗?
质量减小、体积减小,但是密度不变。
特殊:(气体)
一瓶氧气用去一半,它的质量、体积和密度有变化吗?
质量减小、体积不变,密度减小。
二、不变问题
质量不变问题
(如:水结成冰,冰化成水)
体积不变问题
(如:瓶子或容器问题)
密度不变问题
(如:样品问题)
例:求1 m3的冰熔化成水后的体积
思路:冰熔化成水的过程中,质量不变
答:
解:
已知:
求:
V冰=1m3
ρ冰=0.9x103kg/m3
ρ水=1.0x103kg/m3
V水
例:一个瓶子能盛满1kg水,用这个瓶子装满0.8kg某液体,该液体可能是什么?
思路:用同一瓶子两次装满液体的过程中,两种液体的体积相等且等于瓶子的容积。
例:从体积为100cm3质量为300g的物质中取出90g做成零件,求此零件的体积
思路:在从物质中提取部分做零件的过程中,物质的密度不变。
三、空心问题
1、判断空心实心
2、计算空心部分的体积
例:一个铜球的质量是178g,体积为50cm3,这个球是空心的还是实心的?
思路:
解决这类题目的关键就是建立假设条件,可以假定它是实心的,然后从比较密度、质量、体积三个方面考虑
比较密度 比较质量 比较体积
若在上述题目的基础上继续问,若为空心,请计算出空心部分的体积。则如何计算?
上述计算已经计算出178g的铜所占的体积,现在的铜球的体积已知为50cm3,则空心部分的体积即为两者之差。
空心部分 V=V球-V实=50-20=30(cm3)
四、比例计算问题
例:甲乙两物体的体积之比为2:3,质量之比为8:9,求它们的密度之比。
练习1:
甲乙两物体的密度之比为2:3,质量之比为8:9,求它们的体积之比。
练习2:
甲乙两物体的体积之比为2:3,密度之比为8:9,求它们的质量之比。
小明看到煤气公司价格牌上标有“冬季55元/瓶,夏季51元/瓶”的字样。他寻思着,为什么夏季价格低 他查找了煤气资料:煤气冬季密度为0.88×103kg/m3,夏季为0.8×103kg/m3,煤气瓶容积为0.015m3。通过计算发现夏季价格比冬季价格 (高/低)。若夏季价格和冬季一样,夏季应标价为 元/瓶。
五、煤气价格问题:
现在节水型洁具逐渐进入百姓家庭。所谓节水型洁具,是指每冲一次的耗水量在6L以内的洁具。某家庭新安装一耗水量为5L的节水型洁具,而原有的洁具每次耗水为9L。
①1000kg水可供这节水型洁具冲洗多少次?
②该家庭每月节约用水多少kg?(设平均每天用10次,每月按30天计算)
六、耗水量问题:
用盐水选种,要求密度为1.1×103kg/m3盐水,现有体积为20dm3的盐水,称质量23kg,
(1)这样的盐水是否符合要求?
(2)如不符合要求,应该加盐还是加水?
(3)加多少kg
七、盐水问题:
八、含沙量问题:
为测定黄河水的含沙量
是多少,某同
学取了
10dm
3
的黄河水,称得其质量为
10.18kg
,试求黄河水中的含
沙量。
(
ρ
沙
=
2.5
×
10
3
kg/m
3
)
为测定黄河水的含沙量(每立方米含沙多少千克)是多少,某同学取了10dm3的黄河水,称得其质量为10.18kg,试求黄河水中的含沙量。(ρ沙=2.5×103kg/m3)
九、实验:测固体和液体的密度
实验原理:
实验器材:
ρ=
m
V
托盘天平、量筒、烧杯、水、待测物体
实验一、如何测固体(如小石块)的密度
1.用调好的天平测出石块的质量m
2.在量筒内倒入适量的水,测出水的体积V1
3.将石块放入量筒中,测出总体积V2
实验步骤:
4.石块的密度:
V1
V2
实验二、如何测液体(如酒精)的密度
1.用调好的天平测出烧杯和酒精的总质量m1
2.将部分酒精倒入量筒,测出酒精的体积V
3.用天平测出烧杯和剩余酒精的质量m2
实验步骤:
4.酒精的密度:
V
m1-
V
m
=
r
m2
=
m1
m2
★关于密度的特殊测量★
例:现有天平、烧杯、水、未知名液体,如何利用这些仪器测出该液体的密度。
解:①用天平测出空烧杯质量,记为m1。
②在烧杯里倒入水,并作标记,测出质量记为m2,则m水= m2-m1。
③将水倒出,在烧杯里倒入待测液体至标记处,测质量记为m3,则m液= m3-m1。
④
500g冰熔化成水,体积是多少?
一只空瓶子,它的质量是150g,用它装满水,瓶和水的总质量为350g,换它装煤油可装多少?
不用天平只用量筒,能否测出100g的酒精?
一个木球体积为300cm3,质量为100g,它是实心还是空心?(三种解法)
体积是30cm3的空心铜球质量是89g,将它的中心部分注满某种液体后的球的总质量是361g,问注入的液体是什么物质?
同课章节目录
- 第一章 走进物理世界
- 1 希望你喜爱物理
- 2 测量长度和时间
- 3 长度和时间测量的应用
- 4 尝试科学探究
- 第二章 声音与环境
- 1 我们怎样听见声音
- 2 我们怎样区分声音
- 3 我们怎样区分声音(续)
- 4 让声音为人类服务
- 第三章 光和眼睛
- 1 光世界巡行
- 2 探究光的反射规律
- 3 探究平面镜成像特点
- 4 探究光的折射规律
- 5 奇妙的透镜
- 6 探究凸透镜成像规律
- 7 眼睛与光学仪器
- 第四章 物质形态及其变化
- 1 从地球变暖谈起
- 2 探究汽化和液化的特点
- 3 探究熔化和凝固的特点
- 4 升华和凝华
- 5 水循环与水资源
- 第五章 我们周围的物质
- 1 物体的质量
- 2 探究物质的密度
- 3 密度的应用
- 4 认识物质的一些物理属性
- 5 点击新材料
