第二十五章 概率初步 单元达标检测卷(含答案)
文档属性
| 名称 | 第二十五章 概率初步 单元达标检测卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 469.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 17:20:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册单元达标检测卷
第二十五章 概率初步
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
1. 下列事件中,是必然事件的是( )
A.掷一次骰子,向上一面的点数是6
B.13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月
C.射击运动员射击一次,命中靶心
D.经过有交通信号灯的路口,遇到红灯
2. 下列说法正确的是( )
A.若甲、乙两组数据的平均数相同,s甲2=0.1,s乙2=0.04,则乙组数据较稳定
B.如果明天降水的概率是50%,那么明天有半天都在降雨
C.了解全国中学生的节水意识应选用普查方式
D.早上的太阳从西方升起是必然事件
3. 下列说法正确的是( )
A.“若ac=bc,则a=b”是必然事件
B.“若|a|+|b|=0,则a=0且b=0”是不确定事件
C.“若ab=0,则a=0且b=0”是不可能事件
D.“若<0,则a>0且b<0”是随机事件
4. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率( )
A. B. C. D.
5. 不透明袋子中有除颜色外完全相同的4个黑球和2个白球,从袋子中随机摸出3个球,下列事件是必然事件的是( )
A.3个都是黑球 B.2个黑球1个白球
C.2个白球1个黑球 D.至少有1个黑球
6. 下列游戏公平的是( )
A.掷一枚硬币两次,出现两次正面甲胜,出现两次反面乙胜
B.掷一枚硬币两次,出现一次正面甲胜,出现两次反面乙胜
C.掷一枚硬币两次,至少出现一次正面甲胜,出现一次反面一次正面乙胜
D.掷一枚硬币两次,出现相同面甲胜,至少出现一次正面乙胜
7. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
8. 小玲与小丽两人各掷一个正方体骰子,规定两人掷的点数和为偶数,则小玲胜;点数和为奇数,则小丽胜.下列说法正确的是( )
A.此规则有利于小玲 B.此规则有利于小丽
C.此规则对两人是公平的 D.无法判断此规则是否公平
9. 如图所示,小明、小刚利用两个转盘进行游戏,规则为小明将两个转盘各转一次,如配成紫色(红与蓝),小明胜,否则小刚胜,此规则( )
A.公平 B.对小明有利
C.对小刚有利 D.公平性不可预测
10. 同时抛掷完全相同的A,B两个质地均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),两个立方体朝上的数字分别为x,y,并以此确定P(x,y),那么点P落在函数y=-2x+9图象上的概率为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11. “种瓜得瓜,种豆得豆”这一事件是 .(填“必然事件”“不可能事件”或“随机事件”)
12. 一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
13. 有5张无差别的卡片,上面分别标有-1,0,,,π,从中随机抽取1张,则抽出的数是无理数的概率是 .
14. 在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有 个.
15. 小明用0~9中的数字给手机设置了六位开机密码,但他把最后一位数字忘记了,小明只输入一次密码就能打开手机的概率是 .
16. 为了满足广大师生的饮食用餐要求,学校餐厅为师生准备了A,B,C,D四种特制套餐,丁老师和小明同学一起去吃饭,他们每人随机选取一份套餐(套餐量满足师生选择需求),则丁老师和小明选到不同种套餐的概率是 .
17. 如图,随机闭合开关S1,S2,S3中的两个,能让灯泡发光的概率是 .
18. 甲、乙两人玩抽扑克牌游戏,游戏规则是:从一副去掉大小王的扑克牌中,随机抽取一张,若所抽取的牌面数字为奇数,则甲获胜;若所抽取的牌面数字为偶数,则乙获胜(J,Q,K分别代表11,12,13).这个游戏 .(填“公平”或“不公平” )
三、解答题(共66分)
19. (8分)班主任让同学们为班会活动设计一个抽奖方案,拟使中奖概率为50%.
(1)小明的设计方案:在一个不透明的盒子中,放入8个球,这些球除颜色外其他都相同,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有 个.
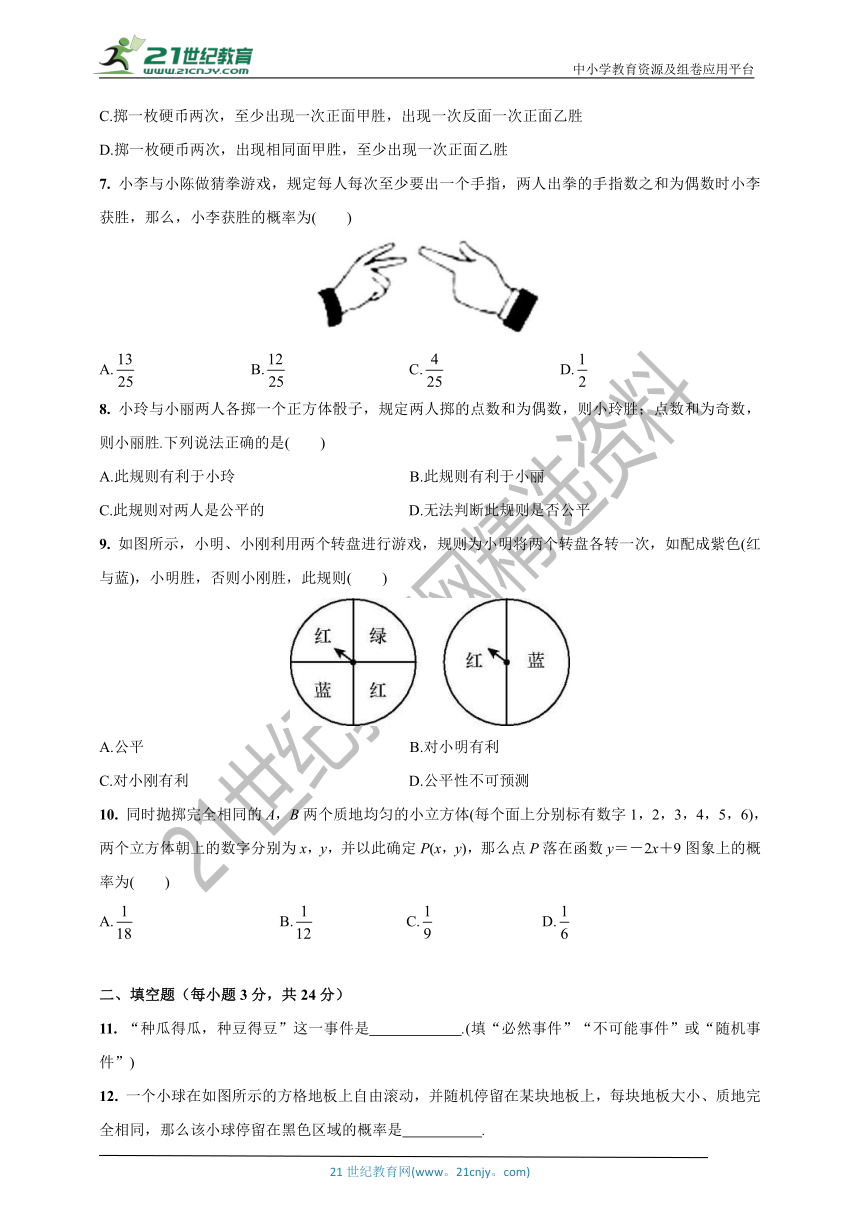
(2)小兵的设计方案:在一个不透明的盒子中,放入3个黄球和1个白球,这些球除颜色外其他都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖.该设计方案是否符合老师的要求 试说明理由.
20. (8分)“每天锻炼一小时,健康生活一辈子”,学校准备从小明和小亮两人中随机选拔一人当“阳光大课间”的领操员,体育老师设计的游戏规则是:四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明两人各抽取一张扑克牌,两张牌面数字之和为奇数时,小亮当选;否则小明当选.
(1)请用画树状图法或列表法求出所有可能的结果.
(2)请问这个游戏规则公平吗 并说明理由.
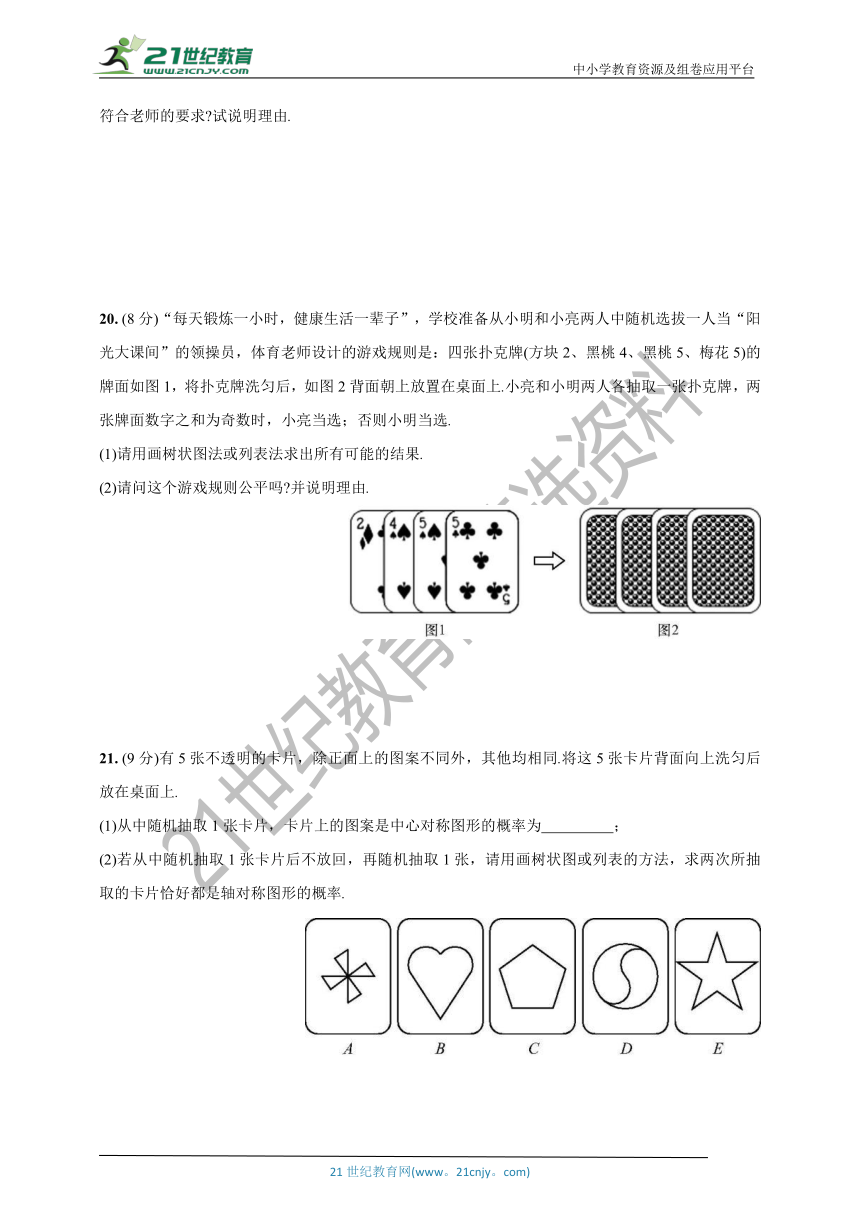
21. (9分)有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为 ;
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
22. (9分)“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A,B,AB,O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 A B AB O
人数 10 5
(1)本次随机抽取献血者人数为 人,图中m= .
(2)补全表中的数据.
(3)若这次活动中该校有1300人义务献血,估计有多少人是A型血
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型.若在4人中随机挑选2人,利用画树状图法或列表法求两人血型均为O型的概率.
23. (10分)湖南全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考,“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考.
(1)“1+2”的选考方案共有多少种 请直接写出所有可能的选法.(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
24. (10分)现有A,B两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球.
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率.
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.
25. (12分)在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).
(1)用列表法或画树状图法表示出(x,y)所有可能出现的结果.
(2)求小明、小华各摸一次扑克牌所确定的一对数满足x+y=5的概率.
(3)小明、小华玩游戏,规则如下:组成数对和为偶数,则小明赢;组成数对和为奇数,则小华赢.你认为这个游戏公平吗 若不公平,请重新设计一个对小明、小华都公平的游戏.
参 考 答 案
1. B 2. A 3. D 4. D 5. D 6. A 7. A 8. C 9. C 10. B
11. 必然事件 12. 13. 14. 7 15. 16. 17. 18. 不公平
19. 解:(1)4
(2)小兵的设计方案符合老师的要求. 理由:由题意,可得小兵设计的方案摸到的2个球都是黄球的概率是,故小兵的设计方案符合老师的要求.
20. 解:(1)画树状图如下:
(2)这个游戏规则不公平.理由如下:由树状图知,共有12种等可能的结果,其中两张牌面数字之和为奇数的有8种情况,所以P(小亮当选)==,P(小明当选)=1-=.因为>,所以这个游戏规则不公平.
21. 解:(1)
(2)画树状图如下:
由树状图知,共有20种等可能结果,其中两次所抽取的卡片恰好都是轴对称图形的有6种结果,∴两次所抽取的卡片恰好都是轴对称图形的概率为.
22. 解:(1)50 20
(2)12 23
(3)1300×=312,这1300人中估计有312人是A型血.
(4)画树状图如下:
所以P(两个O型)==.
23. 解:(1)画树状图如下:
由树状图知,共有12种等可能结果,即“1+2”的选考方案共有12种.
(2)画树状图如下:
由树状图知,共有9种等可能结果,其中他们恰好都选中政治的只有1种结果,所以他们恰好都选中政治的概率为.
24. 解:(1)共有3种等可能结果,而摸出白球的结果有2种,∴P(摸出白球)=.
(2)根据题意,列表如下:
AB 红1 红2 白
白1 (白1,红1) (白1,红2) (白1,白)
白2 (白2,红1) (白2,红2) (白2,白)
红 (红,红1) (红,红2) (红,白)
由上表可知,共有9种等可能结果,其中颜色不同的结果有5种,颜色相同的结果有4种,∴P(颜色不同)=,P(颜色相同)=,∵<,∴这个游戏规则对双方不公平.
25. 解:(1)列表如下:
xy 2 3 4 5
2 (2,2) (3,2) (4,2) (5,2)
3 (2,3) (3,3) (4,3) (5,3)
4 (2,4) (3,4) (4,4) (5,4)
5 (2,5) (3,5) (4,5) (5,5)
由表可得共有16种等可能的结果.
(2)所确定的一对数满足x+y=5的结果有2种:(2,3),(3,2),此事件记作A,则(A)==.
(3)组成数对和为偶数的概率是=,组成数对和为奇数的概率是=,所以游戏公平.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
人教版九年级数学上册单元达标检测卷
第二十五章 概率初步
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
1. 下列事件中,是必然事件的是( )
A.掷一次骰子,向上一面的点数是6
B.13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月
C.射击运动员射击一次,命中靶心
D.经过有交通信号灯的路口,遇到红灯
2. 下列说法正确的是( )
A.若甲、乙两组数据的平均数相同,s甲2=0.1,s乙2=0.04,则乙组数据较稳定
B.如果明天降水的概率是50%,那么明天有半天都在降雨
C.了解全国中学生的节水意识应选用普查方式
D.早上的太阳从西方升起是必然事件
3. 下列说法正确的是( )
A.“若ac=bc,则a=b”是必然事件
B.“若|a|+|b|=0,则a=0且b=0”是不确定事件
C.“若ab=0,则a=0且b=0”是不可能事件
D.“若<0,则a>0且b<0”是随机事件
4. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率( )
A. B. C. D.
5. 不透明袋子中有除颜色外完全相同的4个黑球和2个白球,从袋子中随机摸出3个球,下列事件是必然事件的是( )
A.3个都是黑球 B.2个黑球1个白球
C.2个白球1个黑球 D.至少有1个黑球
6. 下列游戏公平的是( )
A.掷一枚硬币两次,出现两次正面甲胜,出现两次反面乙胜
B.掷一枚硬币两次,出现一次正面甲胜,出现两次反面乙胜
C.掷一枚硬币两次,至少出现一次正面甲胜,出现一次反面一次正面乙胜
D.掷一枚硬币两次,出现相同面甲胜,至少出现一次正面乙胜
7. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
8. 小玲与小丽两人各掷一个正方体骰子,规定两人掷的点数和为偶数,则小玲胜;点数和为奇数,则小丽胜.下列说法正确的是( )
A.此规则有利于小玲 B.此规则有利于小丽
C.此规则对两人是公平的 D.无法判断此规则是否公平
9. 如图所示,小明、小刚利用两个转盘进行游戏,规则为小明将两个转盘各转一次,如配成紫色(红与蓝),小明胜,否则小刚胜,此规则( )
A.公平 B.对小明有利
C.对小刚有利 D.公平性不可预测
10. 同时抛掷完全相同的A,B两个质地均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),两个立方体朝上的数字分别为x,y,并以此确定P(x,y),那么点P落在函数y=-2x+9图象上的概率为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11. “种瓜得瓜,种豆得豆”这一事件是 .(填“必然事件”“不可能事件”或“随机事件”)
12. 一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
13. 有5张无差别的卡片,上面分别标有-1,0,,,π,从中随机抽取1张,则抽出的数是无理数的概率是 .
14. 在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有 个.
15. 小明用0~9中的数字给手机设置了六位开机密码,但他把最后一位数字忘记了,小明只输入一次密码就能打开手机的概率是 .
16. 为了满足广大师生的饮食用餐要求,学校餐厅为师生准备了A,B,C,D四种特制套餐,丁老师和小明同学一起去吃饭,他们每人随机选取一份套餐(套餐量满足师生选择需求),则丁老师和小明选到不同种套餐的概率是 .
17. 如图,随机闭合开关S1,S2,S3中的两个,能让灯泡发光的概率是 .
18. 甲、乙两人玩抽扑克牌游戏,游戏规则是:从一副去掉大小王的扑克牌中,随机抽取一张,若所抽取的牌面数字为奇数,则甲获胜;若所抽取的牌面数字为偶数,则乙获胜(J,Q,K分别代表11,12,13).这个游戏 .(填“公平”或“不公平” )
三、解答题(共66分)
19. (8分)班主任让同学们为班会活动设计一个抽奖方案,拟使中奖概率为50%.
(1)小明的设计方案:在一个不透明的盒子中,放入8个球,这些球除颜色外其他都相同,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有 个.
(2)小兵的设计方案:在一个不透明的盒子中,放入3个黄球和1个白球,这些球除颜色外其他都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖.该设计方案是否符合老师的要求 试说明理由.
20. (8分)“每天锻炼一小时,健康生活一辈子”,学校准备从小明和小亮两人中随机选拔一人当“阳光大课间”的领操员,体育老师设计的游戏规则是:四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明两人各抽取一张扑克牌,两张牌面数字之和为奇数时,小亮当选;否则小明当选.
(1)请用画树状图法或列表法求出所有可能的结果.
(2)请问这个游戏规则公平吗 并说明理由.
21. (9分)有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为 ;
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
22. (9分)“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A,B,AB,O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 A B AB O
人数 10 5
(1)本次随机抽取献血者人数为 人,图中m= .
(2)补全表中的数据.
(3)若这次活动中该校有1300人义务献血,估计有多少人是A型血
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型.若在4人中随机挑选2人,利用画树状图法或列表法求两人血型均为O型的概率.
23. (10分)湖南全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考,“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考.
(1)“1+2”的选考方案共有多少种 请直接写出所有可能的选法.(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
24. (10分)现有A,B两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球.
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率.
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.
25. (12分)在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).
(1)用列表法或画树状图法表示出(x,y)所有可能出现的结果.
(2)求小明、小华各摸一次扑克牌所确定的一对数满足x+y=5的概率.
(3)小明、小华玩游戏,规则如下:组成数对和为偶数,则小明赢;组成数对和为奇数,则小华赢.你认为这个游戏公平吗 若不公平,请重新设计一个对小明、小华都公平的游戏.
参 考 答 案
1. B 2. A 3. D 4. D 5. D 6. A 7. A 8. C 9. C 10. B
11. 必然事件 12. 13. 14. 7 15. 16. 17. 18. 不公平
19. 解:(1)4
(2)小兵的设计方案符合老师的要求. 理由:由题意,可得小兵设计的方案摸到的2个球都是黄球的概率是,故小兵的设计方案符合老师的要求.
20. 解:(1)画树状图如下:
(2)这个游戏规则不公平.理由如下:由树状图知,共有12种等可能的结果,其中两张牌面数字之和为奇数的有8种情况,所以P(小亮当选)==,P(小明当选)=1-=.因为>,所以这个游戏规则不公平.
21. 解:(1)
(2)画树状图如下:
由树状图知,共有20种等可能结果,其中两次所抽取的卡片恰好都是轴对称图形的有6种结果,∴两次所抽取的卡片恰好都是轴对称图形的概率为.
22. 解:(1)50 20
(2)12 23
(3)1300×=312,这1300人中估计有312人是A型血.
(4)画树状图如下:
所以P(两个O型)==.
23. 解:(1)画树状图如下:
由树状图知,共有12种等可能结果,即“1+2”的选考方案共有12种.
(2)画树状图如下:
由树状图知,共有9种等可能结果,其中他们恰好都选中政治的只有1种结果,所以他们恰好都选中政治的概率为.
24. 解:(1)共有3种等可能结果,而摸出白球的结果有2种,∴P(摸出白球)=.
(2)根据题意,列表如下:
AB 红1 红2 白
白1 (白1,红1) (白1,红2) (白1,白)
白2 (白2,红1) (白2,红2) (白2,白)
红 (红,红1) (红,红2) (红,白)
由上表可知,共有9种等可能结果,其中颜色不同的结果有5种,颜色相同的结果有4种,∴P(颜色不同)=,P(颜色相同)=,∵<,∴这个游戏规则对双方不公平.
25. 解:(1)列表如下:
xy 2 3 4 5
2 (2,2) (3,2) (4,2) (5,2)
3 (2,3) (3,3) (4,3) (5,3)
4 (2,4) (3,4) (4,4) (5,4)
5 (2,5) (3,5) (4,5) (5,5)
由表可得共有16种等可能的结果.
(2)所确定的一对数满足x+y=5的结果有2种:(2,3),(3,2),此事件记作A,则(A)==.
(3)组成数对和为偶数的概率是=,组成数对和为奇数的概率是=,所以游戏公平.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
同课章节目录
