函数的单调性第一课时
图片预览


文档简介
(共26张PPT)
O
y
O
x
O
x
y
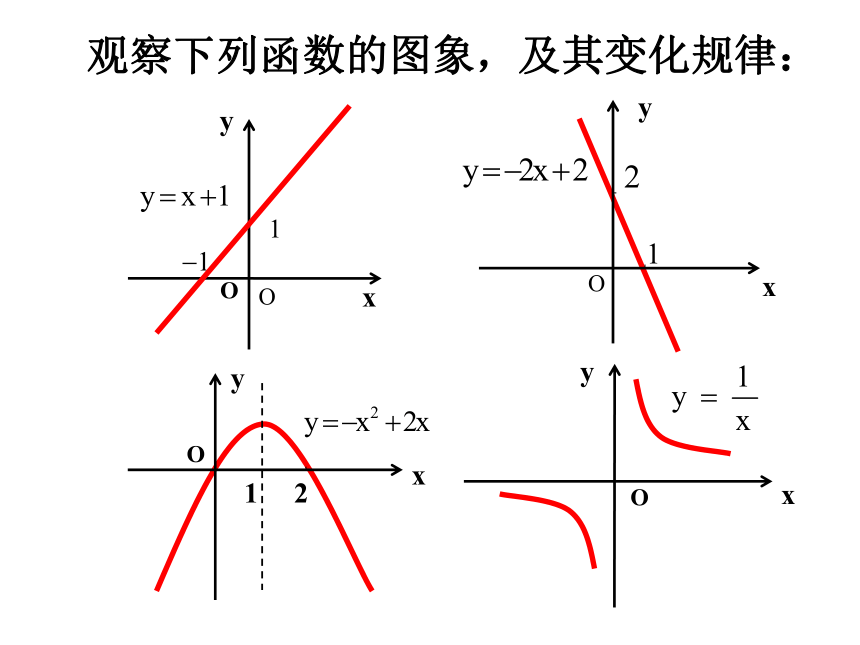
观察下列函数的图象,及其变化规律:
O
x
y
2
1
y
O
x
思考1:如何描述函数图象的“上升”、“下降”
二次函数图象.gsp
以二次函数 图象为例
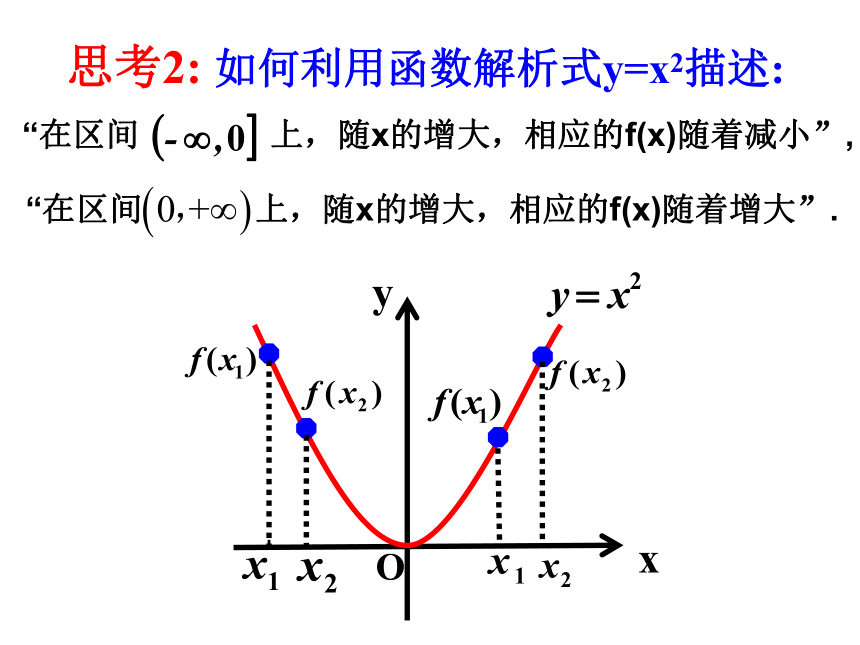
思考2: 如何利用函数解析式y=x2描述:
O
x
y
“在区间 上,随x的增大,相应的f(x)随着减小”,
“在区间 上,随x的增大,相应的f(x)随着增大”.
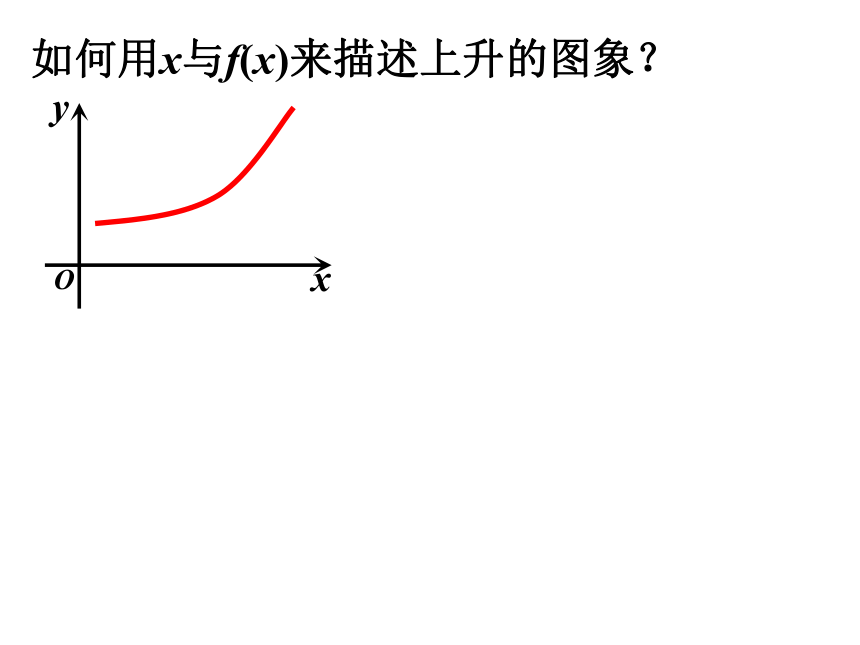
如何用x与f(x)来描述上升的图象?
O
x
y
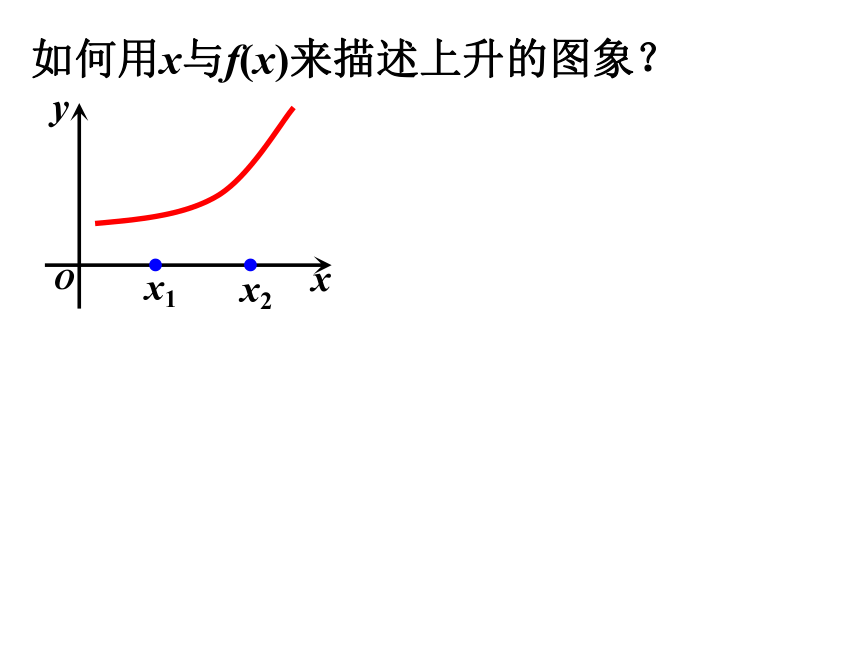
如何用x与f(x)来描述上升的图象?
O
x
y
x2
x1
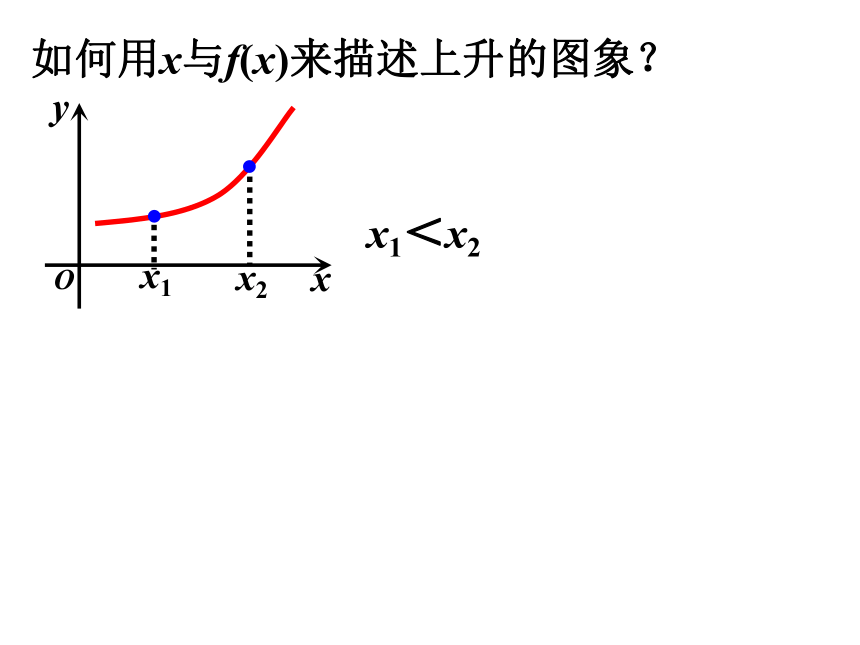
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
x2
x1
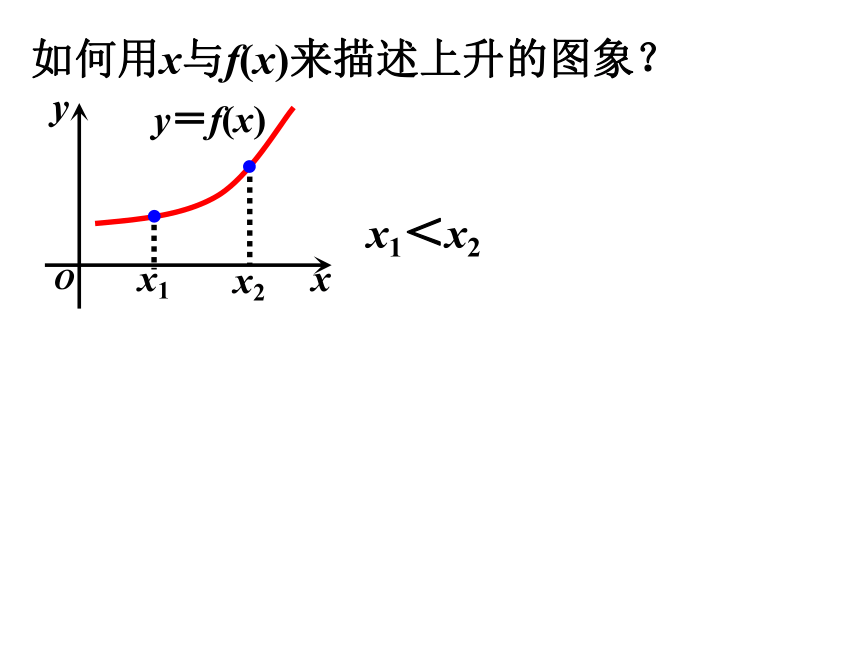
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
y=f(x)
x2
x1
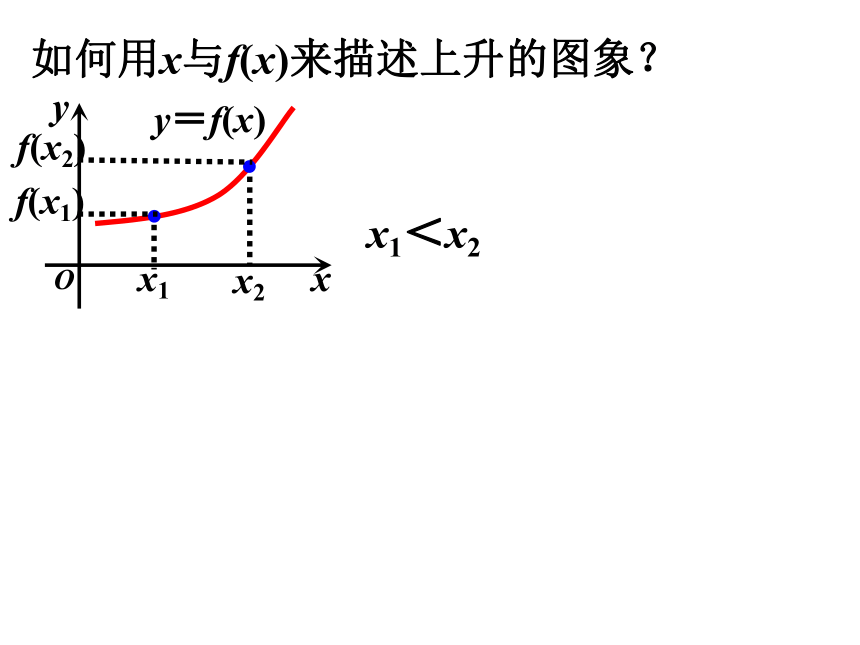
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
y=f(x)
f(x1)
f(x2)
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
y=f(x)
f(x1)
f(x2)
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
y=f(x)
f(x1)
f(x2)
x1<x2 f(x1)<f(x2)
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
y=f(x)
f(x1)
f(x2)
x2
x1
在给定区间上任取x1, x2
x1<x2 f(x1)<f(x2)
函数f (x)在给定区间上为增函数。
如何用x与f(x)来描述上升的图象?
O
x
y
y=f(x)
f(x1)
f(x2)
x2
x1
在给定区间上任取x1, x2
x1<x2 f(x1)<f(x2)
函数f (x)在给定区间上为增函数。
如何用x与f(x)来描述下降的图象?
x2
x1
O
x
y
y=f(x)
f(x1)
f(x2)
x2
x1
函数f (x)在给定区间上为减函数。
x1<x2 f(x1)>f(x2)
在给定区间上任取x1, x2
一、增函数、减函数:
一般地,设函数f(x)的定义域为I。
1.如果对于定义域I内的某个区间D上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间D上是
增函数。
2.如果对于定义域I内的某个区间D上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间D上是
减函数。
二、函数单调性:
-2
1
2
3
4
5
-2
3
-3
-4
-5
-1
-1
1
2
例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,函数y=f(x)是增函数还是减函数。
解:函数f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5]
其中f(x)在区间[-5,-2),[1,3)上是减函数,
在区间[-2,1),[3,5]上是增函数。
图象法
(1)函数的单调性也叫函数的增减性。
(2)函数的单调性是对某个区间而言的,它是个局部概念。
这个区间是定义域的子集。
(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则区间为单调递增区间
若函数在此区间上是减函数,则区间为单调递减区间
(4)单调函数的图像特征(几何特征):
增函数
图像从左向右上升
减函数
图像从左向右下降
O
y
O
x
O
x
y
观察下列函数的图象,及其变化规律:
O
x
y
2
1
y
O
x
增区间为:
减区间为:
增区间为:
减区间为:
减区间为:
函数f(x)=kx+b(k>0)在R上是增函数。
函数f(x)=kx+b(k<0)在R上是减函数。
一次函数 的单调性:
单调增区间 单调减区间
a>0
a<0
的对称轴为
O
x
y
O
x
y
二次函数 的单调性:
k>0
k<0
反比例函数 的单调性:
O
x
y
O
x
y
增函数
增函数
减函数
减函数
结论:函数f(x)= 在其定义域上不具有
单调性。
1、y= - x+5的单调区间。
2、y=4x+5的单调区间。
3、y= - x2+3x+5的单调区间。
例2:证明函数f(x)=3x+2在R上是增函数。
证明:
(设元)
在R上是增函数。
(定论)
任取x1, x2∈R,且x1<x2
(作差)
(变形)
(断号)
3、断号:判断上述差的符号;
4、定论:
1、设元:任取x1, x2∈给定的区间,且x1<x2;
2、作差、变形:计算f(x1)-f(x2) 至最简;
(若差<0,则为增函数;
若差>0,则为减函数)。
三、用定义证明函数单调性的步骤
证明函数f(x)在区间D上具有单调性的步骤:
练习1:判断函数f(x)= 在(0, +∞)上的单调性。
解:
所以函数 在(0,+ )上是减函数。
任取x1, x2∈ (0, +∞) ,且x1<x2
函数 在(0,+ )上是减函数,证明如下:
课堂小结结
1、两个定义:增函数、减函数。
2、两种方法:
判断函数单调性的方法:
有图象法、定义法 。
O
y
O
x
O
x
y
观察下列函数的图象,及其变化规律:
O
x
y
2
1
y
O
x
思考1:如何描述函数图象的“上升”、“下降”
二次函数图象.gsp
以二次函数 图象为例
思考2: 如何利用函数解析式y=x2描述:
O
x
y
“在区间 上,随x的增大,相应的f(x)随着减小”,
“在区间 上,随x的增大,相应的f(x)随着增大”.
如何用x与f(x)来描述上升的图象?
O
x
y
如何用x与f(x)来描述上升的图象?
O
x
y
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
y=f(x)
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
y=f(x)
f(x1)
f(x2)
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
x1<x2
y=f(x)
f(x1)
f(x2)
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
y=f(x)
f(x1)
f(x2)
x1<x2 f(x1)<f(x2)
x2
x1
如何用x与f(x)来描述上升的图象?
O
x
y
y=f(x)
f(x1)
f(x2)
x2
x1
在给定区间上任取x1, x2
x1<x2 f(x1)<f(x2)
函数f (x)在给定区间上为增函数。
如何用x与f(x)来描述上升的图象?
O
x
y
y=f(x)
f(x1)
f(x2)
x2
x1
在给定区间上任取x1, x2
x1<x2 f(x1)<f(x2)
函数f (x)在给定区间上为增函数。
如何用x与f(x)来描述下降的图象?
x2
x1
O
x
y
y=f(x)
f(x1)
f(x2)
x2
x1
函数f (x)在给定区间上为减函数。
x1<x2 f(x1)>f(x2)
在给定区间上任取x1, x2
一、增函数、减函数:
一般地,设函数f(x)的定义域为I。
1.如果对于定义域I内的某个区间D上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间D上是
增函数。
2.如果对于定义域I内的某个区间D上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间D上是
减函数。
二、函数单调性:
-2
1
2
3
4
5
-2
3
-3
-4
-5
-1
-1
1
2
例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,函数y=f(x)是增函数还是减函数。
解:函数f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5]
其中f(x)在区间[-5,-2),[1,3)上是减函数,
在区间[-2,1),[3,5]上是增函数。
图象法
(1)函数的单调性也叫函数的增减性。
(2)函数的单调性是对某个区间而言的,它是个局部概念。
这个区间是定义域的子集。
(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则区间为单调递增区间
若函数在此区间上是减函数,则区间为单调递减区间
(4)单调函数的图像特征(几何特征):
增函数
图像从左向右上升
减函数
图像从左向右下降
O
y
O
x
O
x
y
观察下列函数的图象,及其变化规律:
O
x
y
2
1
y
O
x
增区间为:
减区间为:
增区间为:
减区间为:
减区间为:
函数f(x)=kx+b(k>0)在R上是增函数。
函数f(x)=kx+b(k<0)在R上是减函数。
一次函数 的单调性:
单调增区间 单调减区间
a>0
a<0
的对称轴为
O
x
y
O
x
y
二次函数 的单调性:
k>0
k<0
反比例函数 的单调性:
O
x
y
O
x
y
增函数
增函数
减函数
减函数
结论:函数f(x)= 在其定义域上不具有
单调性。
1、y= - x+5的单调区间。
2、y=4x+5的单调区间。
3、y= - x2+3x+5的单调区间。
例2:证明函数f(x)=3x+2在R上是增函数。
证明:
(设元)
在R上是增函数。
(定论)
任取x1, x2∈R,且x1<x2
(作差)
(变形)
(断号)
3、断号:判断上述差的符号;
4、定论:
1、设元:任取x1, x2∈给定的区间,且x1<x2;
2、作差、变形:计算f(x1)-f(x2) 至最简;
(若差<0,则为增函数;
若差>0,则为减函数)。
三、用定义证明函数单调性的步骤
证明函数f(x)在区间D上具有单调性的步骤:
练习1:判断函数f(x)= 在(0, +∞)上的单调性。
解:
所以函数 在(0,+ )上是减函数。
任取x1, x2∈ (0, +∞) ,且x1<x2
函数 在(0,+ )上是减函数,证明如下:
课堂小结结
1、两个定义:增函数、减函数。
2、两种方法:
判断函数单调性的方法:
有图象法、定义法 。
