苏教版四年级数学下册 七 三角形、平行四边形和梯形 练习十二(教学课件)(共21张PPT)
文档属性
| 名称 | 苏教版四年级数学下册 七 三角形、平行四边形和梯形 练习十二(教学课件)(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 13:20:47 | ||
图片预览




文档简介
(共21张PPT)
练习十二
三角形、平行四边形和梯形
复习回顾
一
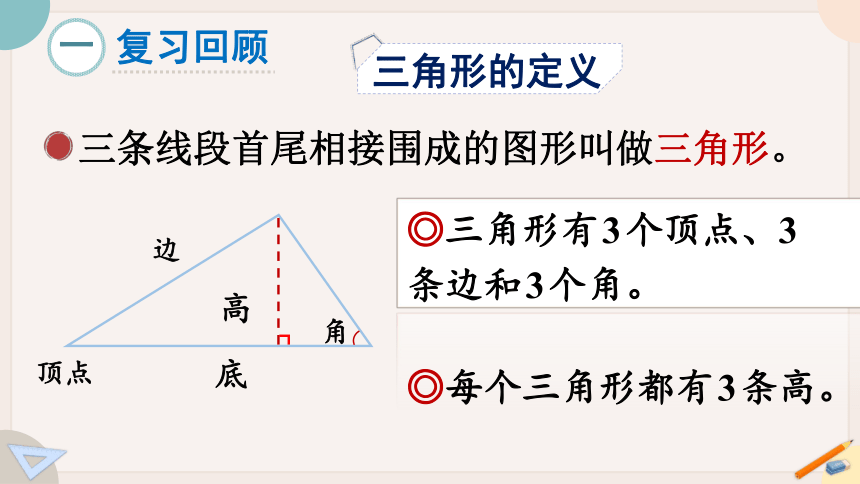
三角形的定义
◎三角形有3个顶点、3条边和3个角。
顶点
边
角
底
高
◎每个三角形都有3条高。
三条线段首尾相接围成的图形叫做三角形。
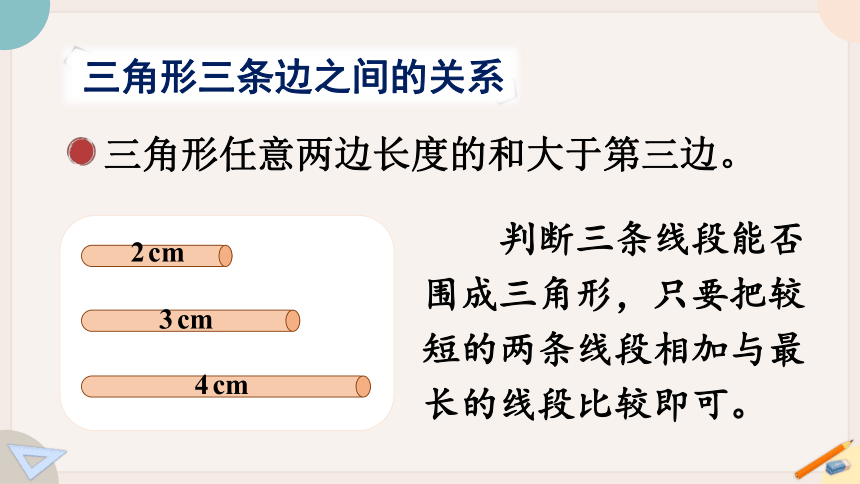
三角形三条边之间的关系
判断三条线段能否围成三角形,只要把较短的两条线段相加与最长的线段比较即可。
2cm
3cm
4cm
三角形任意两边长度的和大于第三边。
三角形的内角和与三角形的大小、形状无关,任意一个三角形的内角和都是180°。
三角形的内角和
强化巩固
二
(教科书第80~81页)
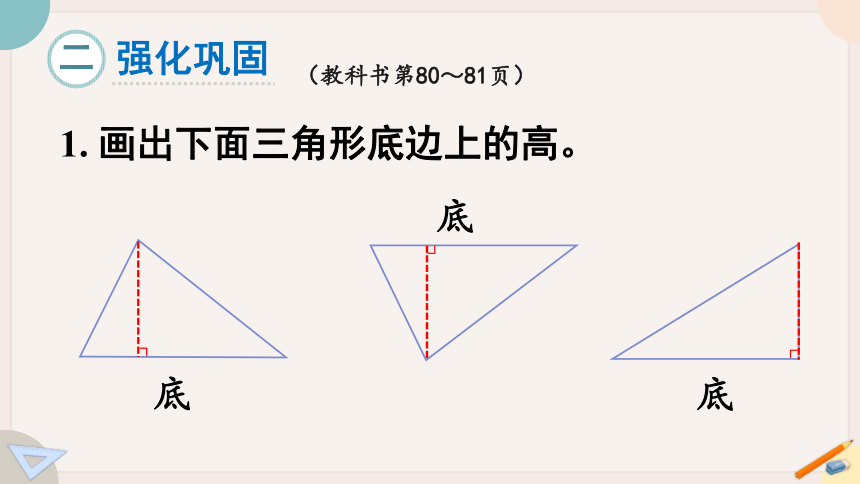
1. 画出下面三角形底边上的高。
底
底
底
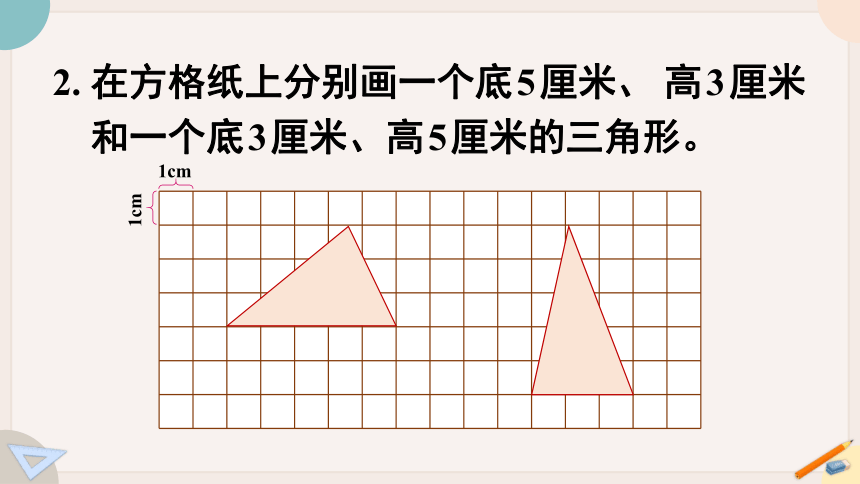
2. 在方格纸上分别画一个底5厘米、 高3厘米
和一个底3厘米、高5厘米的三角形。
1cm
1cm
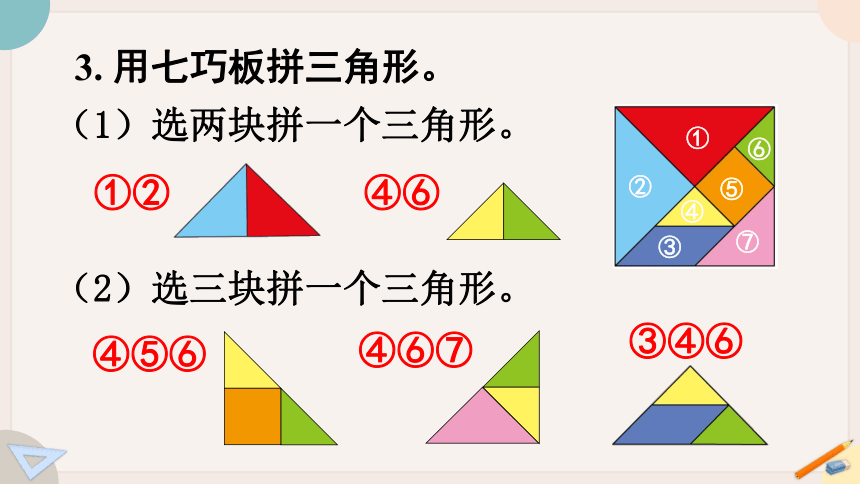
3. 用七巧板拼三角形。
(1)选两块拼一个三角形。
(2)选三块拼一个三角形。
①
②
⑦
③
④
⑤
⑥
①②
④⑥
④⑤⑥
④⑥⑦
③④⑥
(3)你还能用几块拼成一个三角形?
用四块拼:②④⑤⑥
①
②
⑦
③
④
⑤
⑥
②④⑥⑦
②③④⑥
①④⑤⑥
①④⑥⑦
①③④⑥
用五块拼: ③④⑤⑥⑦
用七块拼: ①②③④⑤⑥⑦
★用六块拼不出三角形。
4. 用三根同样长的小棒摆成一个三角形(如右
图),你能说说为什么这个三角形的高一定
比小棒短吗?
点到直线之间,垂直线段最短。
5. 用简便方法计算。
45+187+55
42×102
67×58+33×58
=(45+55)+187
=100+187
=287
=42×(100+2)
=42×100+42×2
=4200+84
=4284
=(67+33)×58
=100×58
=5800
6. 先量出下面的两根小棒的长度,再想一想,
能和它们围成三角形的第三根小棒的长可
能是多少厘米?
提示:先量出两根小棒的长度(可能有误差),再根据三角形的三边关系可知,第三边的长应该大于两边之差,小于两边之和,可以求出第三根小棒的长度范围。
7. 把一根长14厘米的吸管剪成3段(每段都是
整厘米数),用线穿成一个三角形。
可以怎么剪?
5厘米、5厘米、4厘米
6厘米、6厘米、2厘米
6厘米、5厘米、3厘米
6厘米、4厘米、4厘米
提示:三角形最长边必须小于14÷2=7(厘米),如果有一条边长度大于7厘米,则另外两条边的和就会小于7厘米,从而不满足三角形的三边关系。同时最长边必须大于或等于14÷3≈4.7(厘米),如果最长边小于4厘米,则三边的长度之和就会小于14厘米。
8. 从学校到少年宫有几条路线?走哪一条路
最近?
你是怎样想的?
有3条路线,走直线最近。
9.
754000≈( )万
4970000000≈( )亿
75
50
10. 算出每个三角形中未知角的度数。
40°
60°
110°
55°
55°
① 180° 40° 60°=80°
①
②
③
② 180° 110° 55°=15°
③ 180° 90° 55°=35°
11. 一块三角尺的内角和是180°。用两块完
全一样的三角尺拼成一个三角形,拼成的
三角形内角和是多少度?
拼成的三角形内角和是180°。
12. 用一张正方形纸折一折,填一填。
正方形
( )形
( )形
内角和( )°
内角和( )°
内角和( )°
360
三角
三角
180
180
13. 算出下面三角形中∠3的度数。
(1)∠1=42°, ∠2=38°。
(2)∠1=80°, ∠2=56°。
∠3=180° 42° 38°=100°
∠3=180° 80° 56°=44°
课堂小结
三
画高时必须由顶点向它的对边画垂直线段,所画的高用虚线表示,画完后再垂足处标上垂直符号“ ”。
已知三角形中任意两条边的长度,可以确定第三条边的取值范围。
如:设a、b是三角形的任意两条边的长度,则第三条边c的取值范围是:
a bb)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
练习十二
三角形、平行四边形和梯形
复习回顾
一
三角形的定义
◎三角形有3个顶点、3条边和3个角。
顶点
边
角
底
高
◎每个三角形都有3条高。
三条线段首尾相接围成的图形叫做三角形。
三角形三条边之间的关系
判断三条线段能否围成三角形,只要把较短的两条线段相加与最长的线段比较即可。
2cm
3cm
4cm
三角形任意两边长度的和大于第三边。
三角形的内角和与三角形的大小、形状无关,任意一个三角形的内角和都是180°。
三角形的内角和
强化巩固
二
(教科书第80~81页)
1. 画出下面三角形底边上的高。
底
底
底
2. 在方格纸上分别画一个底5厘米、 高3厘米
和一个底3厘米、高5厘米的三角形。
1cm
1cm
3. 用七巧板拼三角形。
(1)选两块拼一个三角形。
(2)选三块拼一个三角形。
①
②
⑦
③
④
⑤
⑥
①②
④⑥
④⑤⑥
④⑥⑦
③④⑥
(3)你还能用几块拼成一个三角形?
用四块拼:②④⑤⑥
①
②
⑦
③
④
⑤
⑥
②④⑥⑦
②③④⑥
①④⑤⑥
①④⑥⑦
①③④⑥
用五块拼: ③④⑤⑥⑦
用七块拼: ①②③④⑤⑥⑦
★用六块拼不出三角形。
4. 用三根同样长的小棒摆成一个三角形(如右
图),你能说说为什么这个三角形的高一定
比小棒短吗?
点到直线之间,垂直线段最短。
5. 用简便方法计算。
45+187+55
42×102
67×58+33×58
=(45+55)+187
=100+187
=287
=42×(100+2)
=42×100+42×2
=4200+84
=4284
=(67+33)×58
=100×58
=5800
6. 先量出下面的两根小棒的长度,再想一想,
能和它们围成三角形的第三根小棒的长可
能是多少厘米?
提示:先量出两根小棒的长度(可能有误差),再根据三角形的三边关系可知,第三边的长应该大于两边之差,小于两边之和,可以求出第三根小棒的长度范围。
7. 把一根长14厘米的吸管剪成3段(每段都是
整厘米数),用线穿成一个三角形。
可以怎么剪?
5厘米、5厘米、4厘米
6厘米、6厘米、2厘米
6厘米、5厘米、3厘米
6厘米、4厘米、4厘米
提示:三角形最长边必须小于14÷2=7(厘米),如果有一条边长度大于7厘米,则另外两条边的和就会小于7厘米,从而不满足三角形的三边关系。同时最长边必须大于或等于14÷3≈4.7(厘米),如果最长边小于4厘米,则三边的长度之和就会小于14厘米。
8. 从学校到少年宫有几条路线?走哪一条路
最近?
你是怎样想的?
有3条路线,走直线最近。
9.
754000≈( )万
4970000000≈( )亿
75
50
10. 算出每个三角形中未知角的度数。
40°
60°
110°
55°
55°
① 180° 40° 60°=80°
①
②
③
② 180° 110° 55°=15°
③ 180° 90° 55°=35°
11. 一块三角尺的内角和是180°。用两块完
全一样的三角尺拼成一个三角形,拼成的
三角形内角和是多少度?
拼成的三角形内角和是180°。
12. 用一张正方形纸折一折,填一填。
正方形
( )形
( )形
内角和( )°
内角和( )°
内角和( )°
360
三角
三角
180
180
13. 算出下面三角形中∠3的度数。
(1)∠1=42°, ∠2=38°。
(2)∠1=80°, ∠2=56°。
∠3=180° 42° 38°=100°
∠3=180° 80° 56°=44°
课堂小结
三
画高时必须由顶点向它的对边画垂直线段,所画的高用虚线表示,画完后再垂足处标上垂直符号“ ”。
已知三角形中任意两条边的长度,可以确定第三条边的取值范围。
如:设a、b是三角形的任意两条边的长度,则第三条边c的取值范围是:
a b
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
