四年级数学下册 七 三角形、平行四边形和梯形 整理与练习 苏教版 课件(23张PPT)
文档属性
| 名称 | 四年级数学下册 七 三角形、平行四边形和梯形 整理与练习 苏教版 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 14:25:14 | ||
图片预览







文档简介
(共23张PPT)
整理与练习
三角形、平行四边形和梯形
整体回顾
一
三角形、平行四边形和梯形
1. 三角形的认识及三边关系
2. 三角形的内角和
3. 三角形的分类
4. 认识平行四边形和梯形
知识梳理
二
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
三角形有3个顶点、3条边和3个角。
每个三角形都有3条高。
顶点
边
角
底
高
三条线段首尾相接围成的图形叫做三角形。
三角形的特点
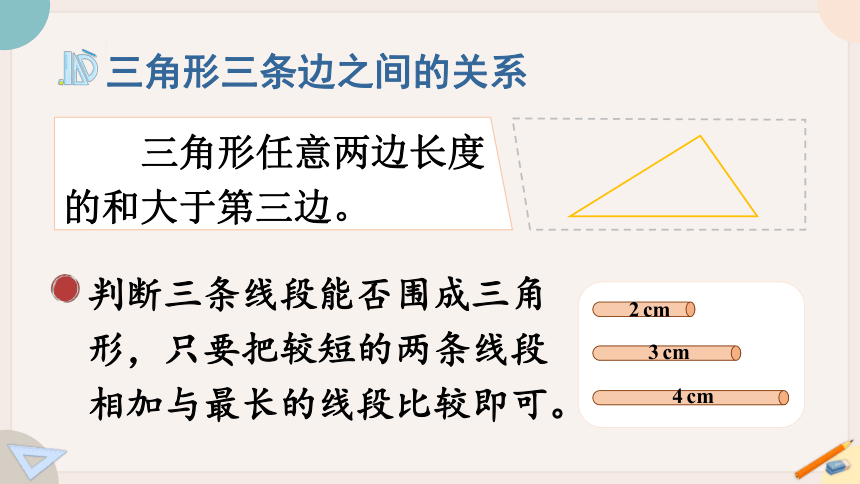
三角形任意两边长度的和大于第三边。
2cm
3cm
4cm
判断三条线段能否围成三角形,只要把较短的两条线段相加与最长的线段比较即可。
三角形三条边之间的关系
三角形的内角和
三角形的内角和与三角形的大小、形状无关,任意一个三角形的内角和都是180°。
三角形的分类
按角分类
钝角三角形:有1个角是钝角的三角形。
锐角三角形:3个角都是锐角的三角形。
直角三角形:有1个角是直角的三角形。
按边分类
不等边三角形
等腰三角形
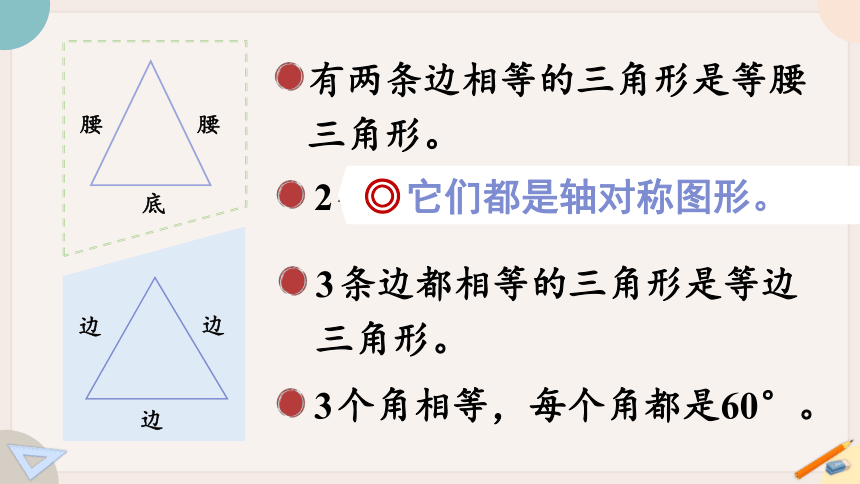
有两条边相等的三角形是等腰三角形。
腰
底
腰
边
边
边
2个底角相等。
3条边都相等的三角形是等边三角形。
3个角相等,每个角都是60°。
◎它们都是轴对称图形。
认识平行四边形
两组对边分别平行的四边形叫作平行四边形。
平行四边形容易变形;
平行四边形有4条边,4个角。
平行四边形的两组对边分别平行且相等。
底
高
从平行四边形一条边上的一点到它对边的垂直线段,是平行四边形的高,这条对边是平行四边形的底。
◎平行四边形有无数条高,而同一底边上的高一定相等。
认识梯形
只有一组对边平行的四边形是梯形。
梯形是四边形,有4条边,4个角;
一组对边平行,另一组对边不平行;
互相平行的一组对边的长度不相等。
在梯形里,互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边分别是梯形的腰。
上底
下底
腰
腰
从梯形一条底边上的一点到它对边的垂直线段叫作梯形的高。
高
两腰相等的梯形是等腰梯形。
综合应用
三
(教科书第93~95页)
1. 下面各题是什么图形?它们有什么不同?分
别画出每个图形底边上的高。
三角形
平行四边形
梯形
高
高
高
不同:三角形由三条边组成,平行四边形和梯形均由四条边组成,平行四边形的两组对边分别平行,而梯形只有一组对边平行。
2. 下面各是什么三角形?根据角的特点怎样分类?
① ② ③ ④ ⑤ ⑥
锐角三角形:
②⑥
①⑤
钝角三角形:
③④
直角三角形:
3.
(1)三角形中,已知∠1=42°,∠2=68°,
求∠3的度数。
∠3=180° 42° 68°=70°
(2)直角三角形中,一个锐角是53°,求另
一个锐角的度数。
180° 90° 53°=37°
(3)等腰三角形的顶角是34°,求它一个
底角的度数。
(180° 34°)÷2=73°
4. 把一根9厘米长的吸管剪成3段(每段都是
整厘米数),围成一个三角形。
(1)能围成多少个不同的三角形?
(2)如果围成等边三角形,边长是多少厘米?
(3)围成等腰三角形,底是多少厘米?
三个。
边长为3厘米。
底是1厘米或3厘米。
5. 彩霞小区有一个花园,由3
个大小不同的等边三角形组
成 (如右图)。从A地到B
地,怎样走最近?哪两条路
一样长?为什么?
走直线最近,因为三角形中两边之和大于第三边。走最左边的路和最右边的路一样长,因为线段的和加起来相等。
6. 把下面的图形补全,使它们成为轴对称图形。
补全后分别是什么图形?
等腰三角形
等腰梯形
平行四边形
7. 你会把一个平行四边形先分成两个图形,再
通过平移得到一个长方形吗?
自己剪一个平行四边形试一试,再与同学交流。
沿着过一个顶点向对边作高的线剪开,平移就可得长方形。
8.
(1)剪出两个完全一样的梯形。
(2)用这两个梯形拼成一个平行四边形。
(3)拼成的平行四边形的底与梯形的上底、
下底有什么关系?拼成的平行四边形
的高与梯形的高呢?
平行四边形=梯形的上底+下底
平行四边形的高=梯形的高
左边是一朵雪花的图案。你知道它是怎样画出来的吗?
先画一个等边三角形,把每条边平均分成3份,以中间的一段为底边,向外再一个等边三角形,并擦去它的底边。向这样画两次,就得到了这个美丽的图案。
(教科书第95页)
在第112页上上试着画一画。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
整理与练习
三角形、平行四边形和梯形
整体回顾
一
三角形、平行四边形和梯形
1. 三角形的认识及三边关系
2. 三角形的内角和
3. 三角形的分类
4. 认识平行四边形和梯形
知识梳理
二
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
三角形有3个顶点、3条边和3个角。
每个三角形都有3条高。
顶点
边
角
底
高
三条线段首尾相接围成的图形叫做三角形。
三角形的特点
三角形任意两边长度的和大于第三边。
2cm
3cm
4cm
判断三条线段能否围成三角形,只要把较短的两条线段相加与最长的线段比较即可。
三角形三条边之间的关系
三角形的内角和
三角形的内角和与三角形的大小、形状无关,任意一个三角形的内角和都是180°。
三角形的分类
按角分类
钝角三角形:有1个角是钝角的三角形。
锐角三角形:3个角都是锐角的三角形。
直角三角形:有1个角是直角的三角形。
按边分类
不等边三角形
等腰三角形
有两条边相等的三角形是等腰三角形。
腰
底
腰
边
边
边
2个底角相等。
3条边都相等的三角形是等边三角形。
3个角相等,每个角都是60°。
◎它们都是轴对称图形。
认识平行四边形
两组对边分别平行的四边形叫作平行四边形。
平行四边形容易变形;
平行四边形有4条边,4个角。
平行四边形的两组对边分别平行且相等。
底
高
从平行四边形一条边上的一点到它对边的垂直线段,是平行四边形的高,这条对边是平行四边形的底。
◎平行四边形有无数条高,而同一底边上的高一定相等。
认识梯形
只有一组对边平行的四边形是梯形。
梯形是四边形,有4条边,4个角;
一组对边平行,另一组对边不平行;
互相平行的一组对边的长度不相等。
在梯形里,互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边分别是梯形的腰。
上底
下底
腰
腰
从梯形一条底边上的一点到它对边的垂直线段叫作梯形的高。
高
两腰相等的梯形是等腰梯形。
综合应用
三
(教科书第93~95页)
1. 下面各题是什么图形?它们有什么不同?分
别画出每个图形底边上的高。
三角形
平行四边形
梯形
高
高
高
不同:三角形由三条边组成,平行四边形和梯形均由四条边组成,平行四边形的两组对边分别平行,而梯形只有一组对边平行。
2. 下面各是什么三角形?根据角的特点怎样分类?
① ② ③ ④ ⑤ ⑥
锐角三角形:
②⑥
①⑤
钝角三角形:
③④
直角三角形:
3.
(1)三角形中,已知∠1=42°,∠2=68°,
求∠3的度数。
∠3=180° 42° 68°=70°
(2)直角三角形中,一个锐角是53°,求另
一个锐角的度数。
180° 90° 53°=37°
(3)等腰三角形的顶角是34°,求它一个
底角的度数。
(180° 34°)÷2=73°
4. 把一根9厘米长的吸管剪成3段(每段都是
整厘米数),围成一个三角形。
(1)能围成多少个不同的三角形?
(2)如果围成等边三角形,边长是多少厘米?
(3)围成等腰三角形,底是多少厘米?
三个。
边长为3厘米。
底是1厘米或3厘米。
5. 彩霞小区有一个花园,由3
个大小不同的等边三角形组
成 (如右图)。从A地到B
地,怎样走最近?哪两条路
一样长?为什么?
走直线最近,因为三角形中两边之和大于第三边。走最左边的路和最右边的路一样长,因为线段的和加起来相等。
6. 把下面的图形补全,使它们成为轴对称图形。
补全后分别是什么图形?
等腰三角形
等腰梯形
平行四边形
7. 你会把一个平行四边形先分成两个图形,再
通过平移得到一个长方形吗?
自己剪一个平行四边形试一试,再与同学交流。
沿着过一个顶点向对边作高的线剪开,平移就可得长方形。
8.
(1)剪出两个完全一样的梯形。
(2)用这两个梯形拼成一个平行四边形。
(3)拼成的平行四边形的底与梯形的上底、
下底有什么关系?拼成的平行四边形
的高与梯形的高呢?
平行四边形=梯形的上底+下底
平行四边形的高=梯形的高
左边是一朵雪花的图案。你知道它是怎样画出来的吗?
先画一个等边三角形,把每条边平均分成3份,以中间的一段为底边,向外再一个等边三角形,并擦去它的底边。向这样画两次,就得到了这个美丽的图案。
(教科书第95页)
在第112页上上试着画一画。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
