苏教版四年级数学下册7.3 三角形的内角和(教学课件)(共16张PPT)
文档属性
| 名称 | 苏教版四年级数学下册7.3 三角形的内角和(教学课件)(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
第3课时 三角形的内角和
三角形、平行四边形和梯形
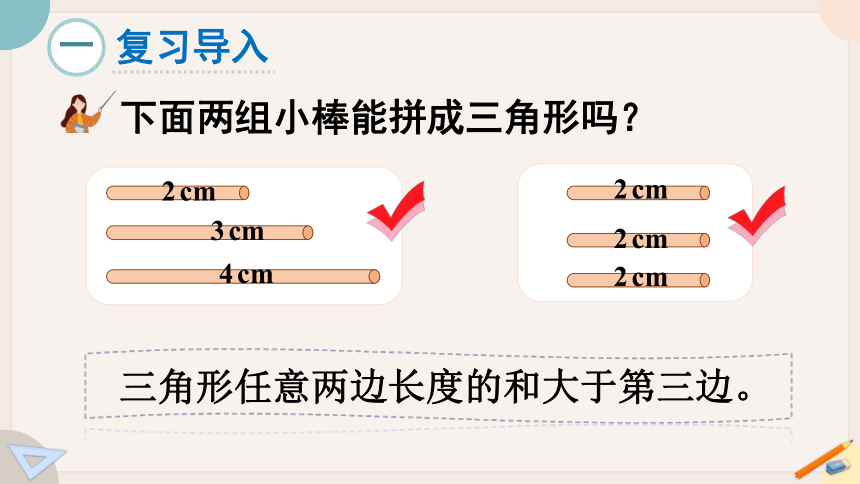
复习导入
一
下面两组小棒能拼成三角形吗?
2cm
3cm
4cm
2cm
2cm
2cm
三角形任意两边长度的和大于第三边。
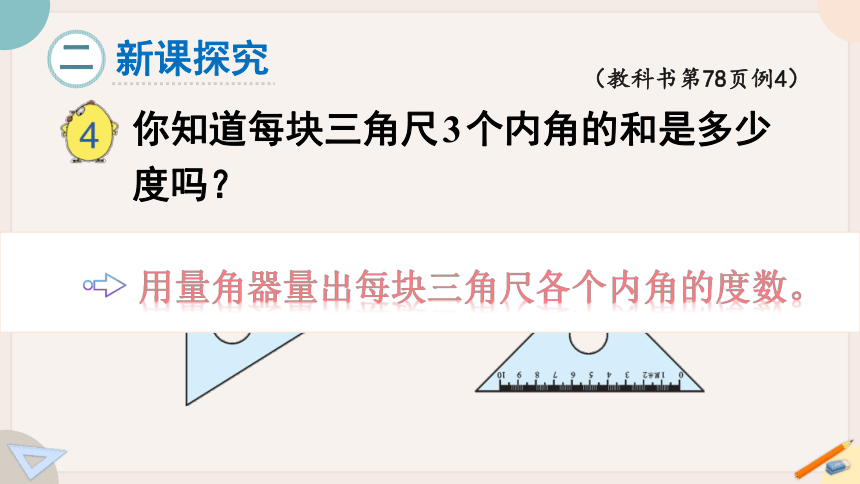
新课探究
二
(教科书第78页例4)
你知道每块三角尺3个内角的和是多少度吗?
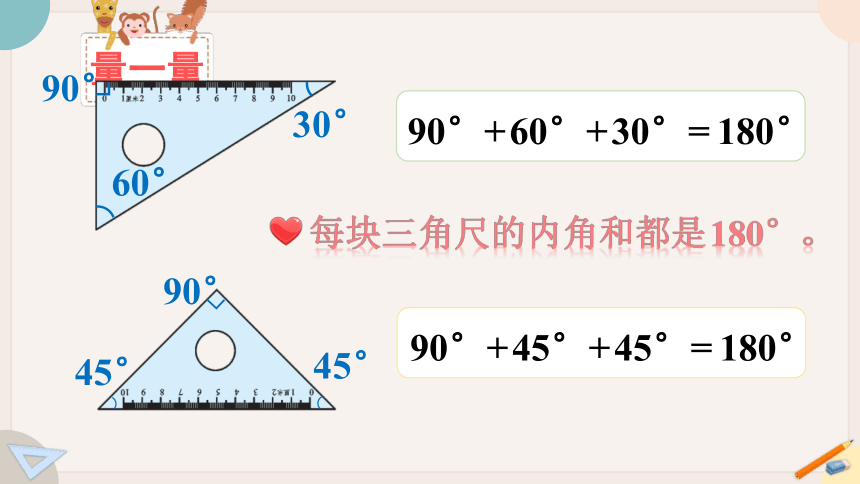
量一量
60°
30°
90°
90°
45°
45°
90°+60°+30°=180°
90°+45°+45°=180°
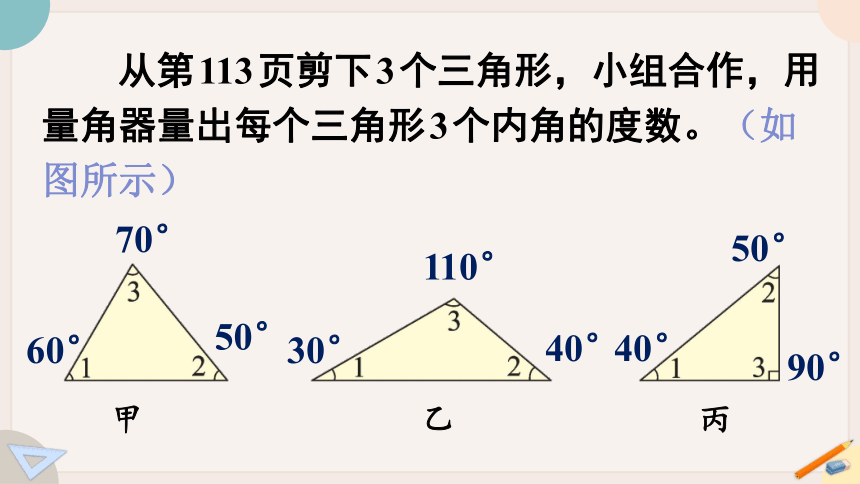
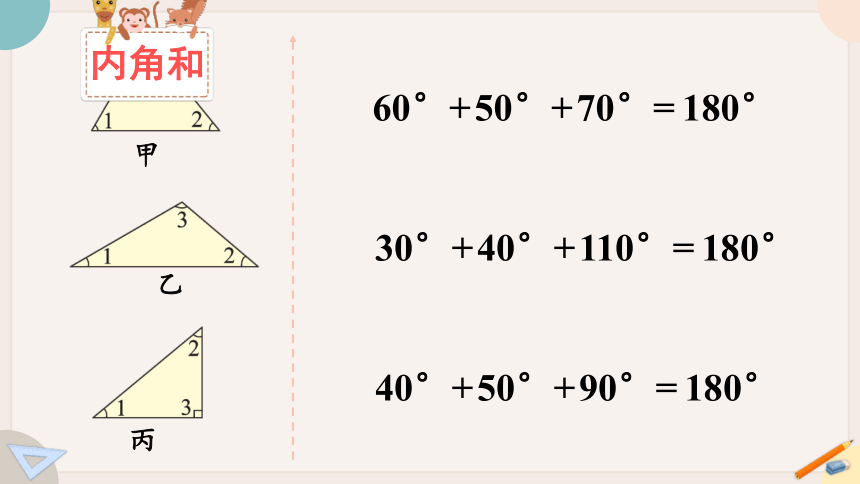
从第113页剪下3个三角形,小组合作,用量角器量出每个三角形3个内角的度数。(如图所示)
甲
乙
丙
60°
50°
70°
30°
40°
110°
40°
90°
50°
甲
乙
丙
60°+50°+70°=180°
30°+40°+110°=180°
40°+50°+90°=180°
内角和
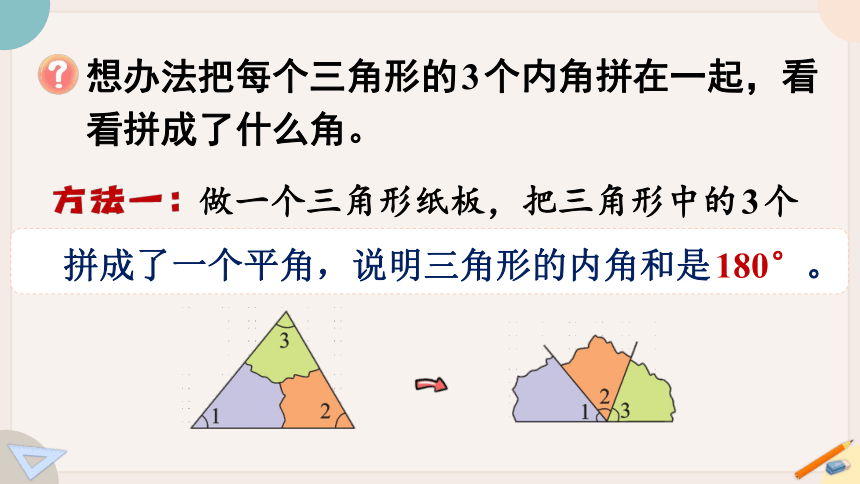
想办法把每个三角形的3个内角拼在一起,看看拼成了什么角。
做一个三角形纸板,把三角形中的3个内角撕下来,标上号,按顺序拼接起来。
拼成了一个平角,说明三角形的内角和是180°。
折一折,拼一拼。
三个内角折到一起正好是平角,说明三角形的内角和是180°。
三角形的内角和与三角形的大小、形状无关,任意一个三角形的内角和都是180°。
随堂练习
三
(教科书第78页练一练)
1. 下边三角形中,∠1=75°,∠2=40°,
∠3=( )°
65
生活中, 许多物体上都有三角形的结构。这是因为三角形具有稳定性,也就是当一个三角形三条边的长度确定后,这个三角形的形状和大小就不会改变。
我们可以做这样一个实验:用三根木条钉一个三角形框架,用力去拉,看看三角形框架的形状会不会改变。
培优训练
四
一、已知∠1、∠2、∠3是同一个三角形的三
个内角。
1. ∠1=34°, ∠2=48° ,则∠3=( )°
2. ∠1=46°, ∠3=96° ,则∠2=( )°
3. ∠3=27°, ∠2=63° ,则∠1=( )°
4. ∠1+ ∠2=170° ,则∠3=( )°
98
38
90
10
二、如图所示,已知∠1=35°,求∠2、 ∠3
的度数。
1
2
3
∠3=180° 90° ∠1
=180° 90° 35°
=55°
∠2=180° 90° ∠3=180° 90° 55°
=35°
课堂小结
五
(1)三角形的内角和与大小、形状无关,三角
形的内角和都等于180°。
三角形的内角和
(2)已知三角形的两个内角和的度数,可以根
据三角形的内角和求出第三个角的度数。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
第3课时 三角形的内角和
三角形、平行四边形和梯形
复习导入
一
下面两组小棒能拼成三角形吗?
2cm
3cm
4cm
2cm
2cm
2cm
三角形任意两边长度的和大于第三边。
新课探究
二
(教科书第78页例4)
你知道每块三角尺3个内角的和是多少度吗?
量一量
60°
30°
90°
90°
45°
45°
90°+60°+30°=180°
90°+45°+45°=180°
从第113页剪下3个三角形,小组合作,用量角器量出每个三角形3个内角的度数。(如图所示)
甲
乙
丙
60°
50°
70°
30°
40°
110°
40°
90°
50°
甲
乙
丙
60°+50°+70°=180°
30°+40°+110°=180°
40°+50°+90°=180°
内角和
想办法把每个三角形的3个内角拼在一起,看看拼成了什么角。
做一个三角形纸板,把三角形中的3个内角撕下来,标上号,按顺序拼接起来。
拼成了一个平角,说明三角形的内角和是180°。
折一折,拼一拼。
三个内角折到一起正好是平角,说明三角形的内角和是180°。
三角形的内角和与三角形的大小、形状无关,任意一个三角形的内角和都是180°。
随堂练习
三
(教科书第78页练一练)
1. 下边三角形中,∠1=75°,∠2=40°,
∠3=( )°
65
生活中, 许多物体上都有三角形的结构。这是因为三角形具有稳定性,也就是当一个三角形三条边的长度确定后,这个三角形的形状和大小就不会改变。
我们可以做这样一个实验:用三根木条钉一个三角形框架,用力去拉,看看三角形框架的形状会不会改变。
培优训练
四
一、已知∠1、∠2、∠3是同一个三角形的三
个内角。
1. ∠1=34°, ∠2=48° ,则∠3=( )°
2. ∠1=46°, ∠3=96° ,则∠2=( )°
3. ∠3=27°, ∠2=63° ,则∠1=( )°
4. ∠1+ ∠2=170° ,则∠3=( )°
98
38
90
10
二、如图所示,已知∠1=35°,求∠2、 ∠3
的度数。
1
2
3
∠3=180° 90° ∠1
=180° 90° 35°
=55°
∠2=180° 90° ∠3=180° 90° 55°
=35°
课堂小结
五
(1)三角形的内角和与大小、形状无关,三角
形的内角和都等于180°。
三角形的内角和
(2)已知三角形的两个内角和的度数,可以根
据三角形的内角和求出第三个角的度数。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
