五年级下册 7.1 用转化的策略解决不规则图形的计算问题 苏教版 课件(17张PPT)
文档属性
| 名称 | 五年级下册 7.1 用转化的策略解决不规则图形的计算问题 苏教版 课件(17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 16:02:53 | ||
图片预览



文档简介
(共17张PPT)
第1课时 用转化的策略解决不规
则图形的计算问题
苏教版数学五年级下册
解决问题的策略
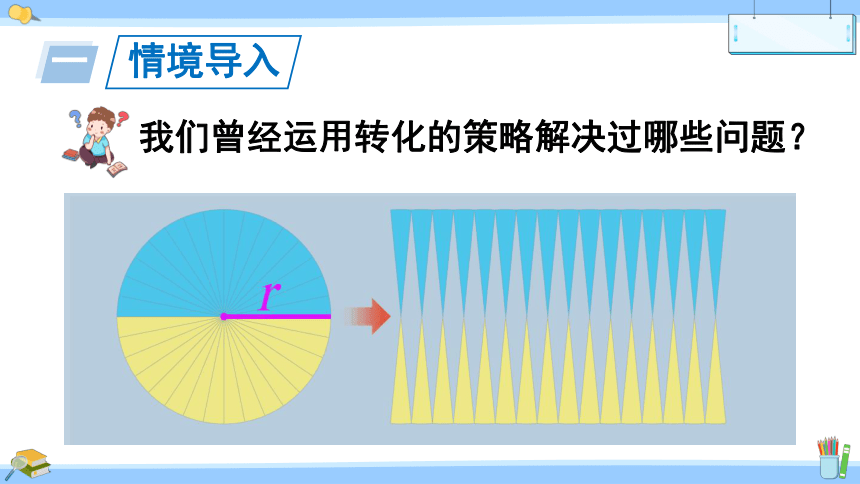
我们曾经运用转化的策略解决过哪些问题?
我们曾经运用转化的策略解决过哪些问题?
(教科书第105页例1)
1
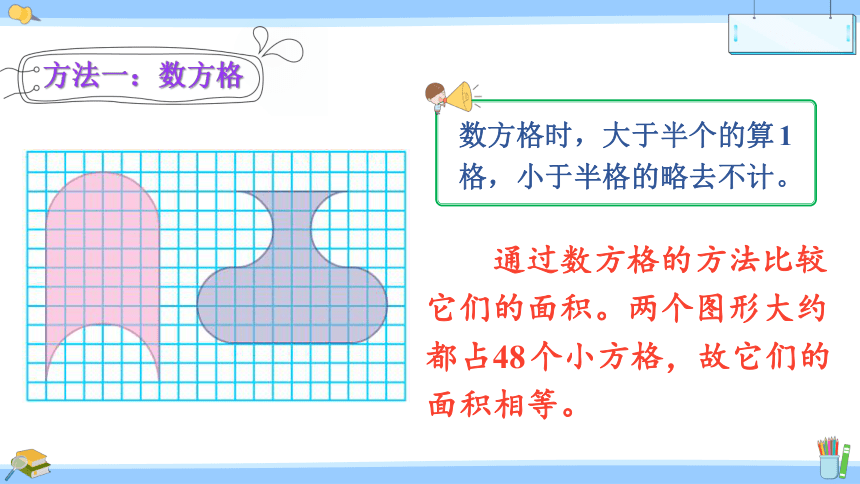
下面两个图形,哪个面积大一些?
你打算怎样比较这两个图形的面积?
方法一:数方格
数方格时,大于半个的算1格,小于半格的略去不计。
通过数方格的方法比较它们的面积。两个图形大约都占48个小方格,故它们的面积相等。
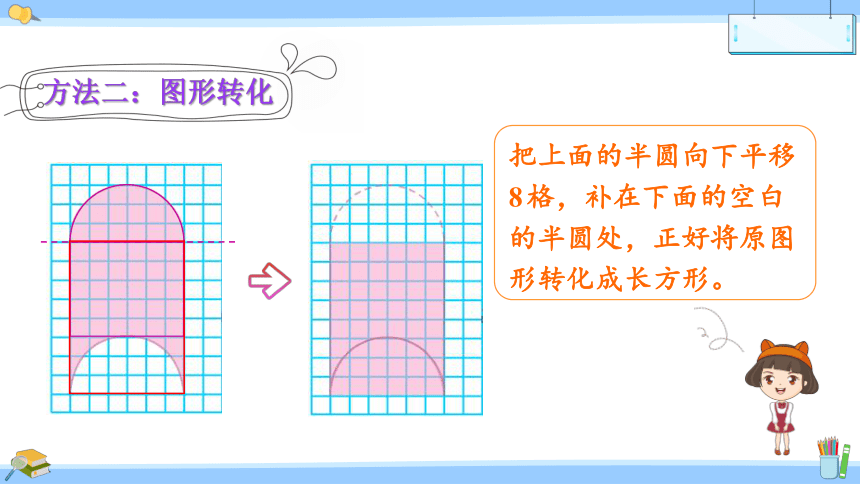
方法二:图形转化
把上面的半圆向下平移8格,补在下面的空白的半圆处,正好将原图形转化成长方形。
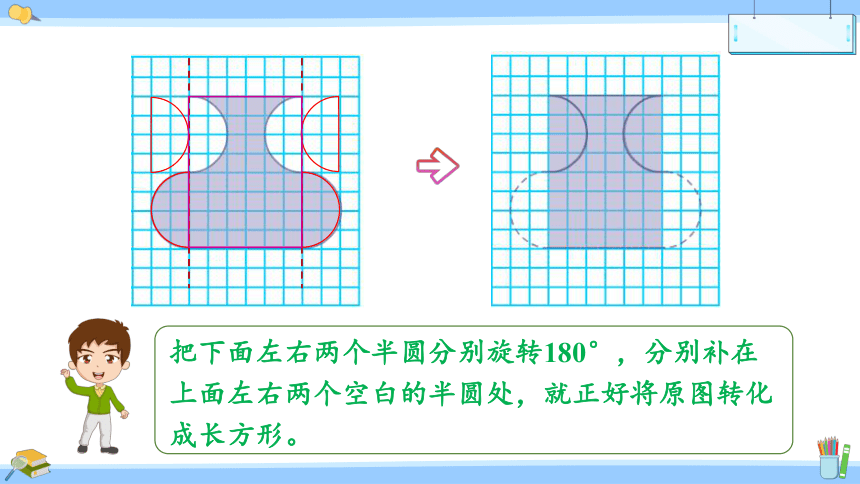
把下面左右两个半圆分别旋转180°,分别补在上面左右两个空白的半圆处,就正好将原图转化成长方形。
先把它们转化成规则图形再比较它们的面积。两个图形都可以转化成长8个方格,宽6个方格的长方形,这两个长方形的面积相等,则原来两个图形的面积相等。
解决此类问题可以运用转化的策略将不规则的图形转化成规则的图形后,再进行计算和比较。转化时可以运用平移、旋转等方法。转化后的图形与转化前相比,形状变了,大小没有变。
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
推导圆面积公式时,把圆转化成长方形。
计算小数乘法时,把小数乘法转化成整数乘法。
(教科书第106页练一练)
1.
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
这两个图案的面积相等。
2.
用分数表示下列各图形中的阴影部分。
1.
求下列各图中阴影部分的面积。(单位:cm)
10×5=50(cm )
2×2=4(cm )
3.14×(6÷2) ÷2+3.14×(8÷2)
=39.25(cm )
2.
如右图所示,已知圆的面积是62.8平方厘米,求正方形的面积。
3.14×r =62.8
解:设圆的半径为r。
r =20
正方形的面积为:
r ÷2×4=20÷2×4=40(cm )
答:正方形的面积是40平方厘米。
在计算不规则图形的面积和周长时,通常要对不规则图形进行平移或旋转,使之变成已知的或较简单的图形后再进行计算。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
第1课时 用转化的策略解决不规
则图形的计算问题
苏教版数学五年级下册
解决问题的策略
我们曾经运用转化的策略解决过哪些问题?
我们曾经运用转化的策略解决过哪些问题?
(教科书第105页例1)
1
下面两个图形,哪个面积大一些?
你打算怎样比较这两个图形的面积?
方法一:数方格
数方格时,大于半个的算1格,小于半格的略去不计。
通过数方格的方法比较它们的面积。两个图形大约都占48个小方格,故它们的面积相等。
方法二:图形转化
把上面的半圆向下平移8格,补在下面的空白的半圆处,正好将原图形转化成长方形。
把下面左右两个半圆分别旋转180°,分别补在上面左右两个空白的半圆处,就正好将原图转化成长方形。
先把它们转化成规则图形再比较它们的面积。两个图形都可以转化成长8个方格,宽6个方格的长方形,这两个长方形的面积相等,则原来两个图形的面积相等。
解决此类问题可以运用转化的策略将不规则的图形转化成规则的图形后,再进行计算和比较。转化时可以运用平移、旋转等方法。转化后的图形与转化前相比,形状变了,大小没有变。
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
推导圆面积公式时,把圆转化成长方形。
计算小数乘法时,把小数乘法转化成整数乘法。
(教科书第106页练一练)
1.
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
这两个图案的面积相等。
2.
用分数表示下列各图形中的阴影部分。
1.
求下列各图中阴影部分的面积。(单位:cm)
10×5=50(cm )
2×2=4(cm )
3.14×(6÷2) ÷2+3.14×(8÷2)
=39.25(cm )
2.
如右图所示,已知圆的面积是62.8平方厘米,求正方形的面积。
3.14×r =62.8
解:设圆的半径为r。
r =20
正方形的面积为:
r ÷2×4=20÷2×4=40(cm )
答:正方形的面积是40平方厘米。
在计算不规则图形的面积和周长时,通常要对不规则图形进行平移或旋转,使之变成已知的或较简单的图形后再进行计算。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
