2021—2022学年人教版数学八年级上册12.2.3三角形全等的判定教学设计
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册12.2.3三角形全等的判定教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 112.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览

文档简介
《12.2.3三角形全等判定》教学设计
课题:12.2.3三角形全等判定 课型:新授课 课时:第一课时
【教学过程】
新课导入
小明家有一块三角形的玻璃破了,要到玻璃店配制同样大小的玻璃。小明量了两角和其中一角的对边到玻璃店,
你猜师傅能配出来吗?
新知探究
先任意画一个△ABC.再画一个△A′B′C′.使A′B′=AB.∠A′= ∠A.∠B′=∠B.(即两角和它们的夹边对应相等).把画好的△A′B′C′.剪下,放到△ABC上,它们全等吗?
1、画A′B′=AB .
2、在A′B′同旁画∠DA′B′=∠A.∠EB′A′=∠B.
A′D.B′E交于点C′.
两角及夹边对应相等的两个三角形全等(ASA).
符号语言:证明:在△ABC与△A B C 中
∠A=∠A‘ AB=A’ B‘
∠B=∠B’
∴△ABC≌△A’B’C’(ASA)
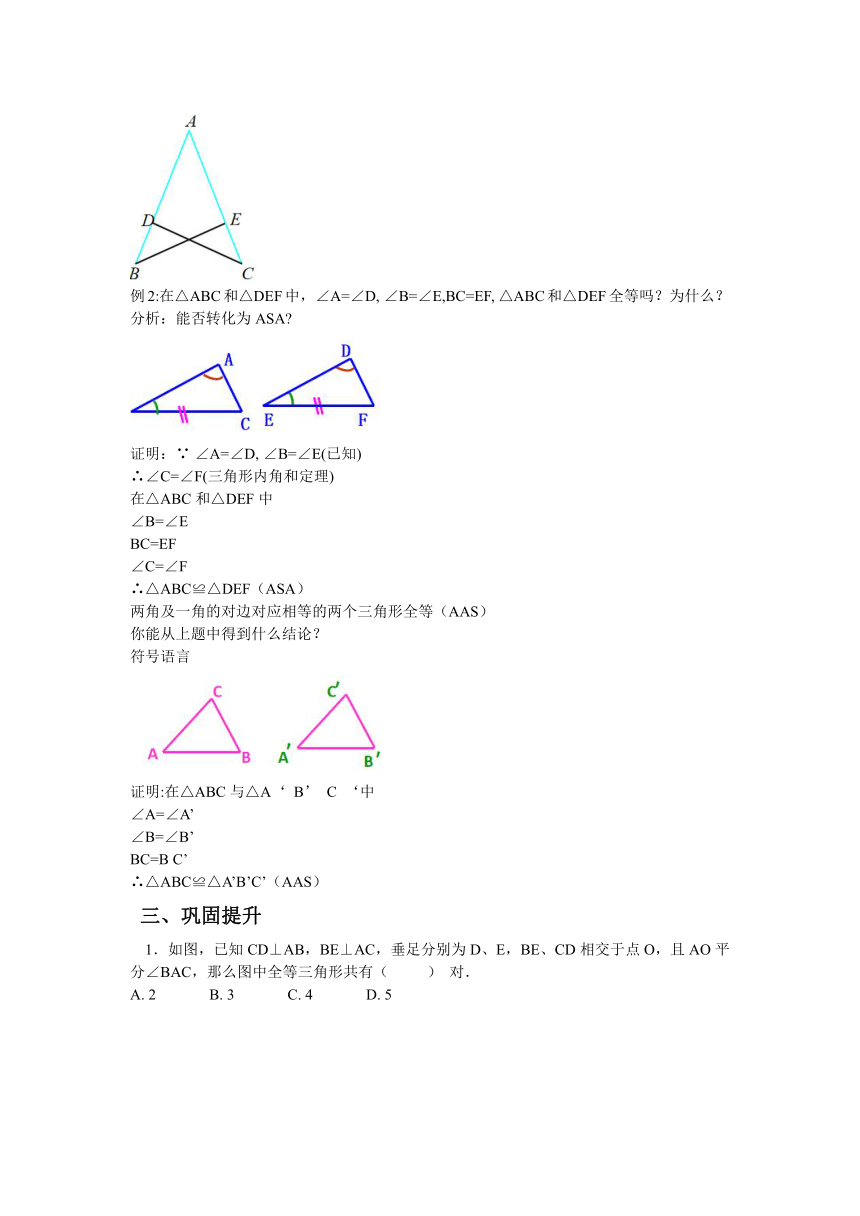
例1:如图,点D 在AB上,点E 在AC上,BA =AC,∠B =∠C.
求证:AD =AE.
证明:在△ABE 和△ACD 中,
∠B =∠C,
AB =AC ,
∠A =∠A ,
∴△ABE ≌△ACD(ASA).
∴AE =AD.
例2:在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?
分析:能否转化为ASA
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理)
在△ABC和△DEF中
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
两角及一角的对边对应相等的两个三角形全等(AAS)
你能从上题中得到什么结论?
符号语言
证明:在△ABC与△A‘ B’ C ‘中
∠A=∠A’
∠B=∠B’
BC=B C’
∴△ABC≌△A’B’C’(AAS)
三、巩固提升
1.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( ) 对.
A. 2 B. 3 C. 4 D. 5
解析:∵CD⊥AB,BE⊥AC,AO平分∠BAC
∴∠ADO=∠AEO=90°,∠DAO=∠EAO
∵AO=AO∴△ADO≌△AEO(AAS)
∴OD=OE,AD=AE
∵∠DOB=∠EOC,∠ODB=∠OEC=90° ∴△BOD≌△COE(ASA)
∴BD=CE,OB=OC,∠B=∠C
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°
∴△ADC≌△AEB(ASA)
∵AD=AE,BD=CE;∴AB=AC
∵OB=OC,AO=AO∴△ABO≌△ACO(SSS)。所以共有四对全等三角形。
故选C。
2、如图,在下列条件中,不能直接证明△ABD≌△ACD的是( )
A. BD=DC,AB=AC
B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD
D. ∠B=∠C,BD=DC
解:∵AD=AD,
A、当BD=DC,AB=AC时,利用SSS证明△ABD≌△ACD,正确;
B、当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD≌△ACD,正确;
C、当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD≌△ACD,正确;
D、当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD≌△ACD,错误.
故选D.
3. △ABC是等腰三角形,AD、BE 分别是∠A、∠B 的角平分线,△ABD和△BAE 全等吗?试说明理由.
∵ △ABC是等腰三角形
∴ AC=BC ∠A=∠B
又∵ AD、BE 分别是∠A、∠B 的角平分线
∴ ∠BAD=1/2 ∠A
∠ABE= 1/2 ∠B
∴ ∠BAD =∠ABE
BAD =∠ABE
AB为公共边
∠EAB=∠DBA
∴△ABD≌△BAE (ASA)
四、课堂小结
1、三角形全等判定
2、隐含条件的找法公共角或部分共角
3、三角形全等条件应用:
通过证明三角形全等,从而证明相关的边相等或角相等
课题:12.2.3三角形全等判定 课型:新授课 课时:第一课时
【教学过程】
新课导入
小明家有一块三角形的玻璃破了,要到玻璃店配制同样大小的玻璃。小明量了两角和其中一角的对边到玻璃店,
你猜师傅能配出来吗?
新知探究
先任意画一个△ABC.再画一个△A′B′C′.使A′B′=AB.∠A′= ∠A.∠B′=∠B.(即两角和它们的夹边对应相等).把画好的△A′B′C′.剪下,放到△ABC上,它们全等吗?
1、画A′B′=AB .
2、在A′B′同旁画∠DA′B′=∠A.∠EB′A′=∠B.
A′D.B′E交于点C′.
两角及夹边对应相等的两个三角形全等(ASA).
符号语言:证明:在△ABC与△A B C 中
∠A=∠A‘ AB=A’ B‘
∠B=∠B’
∴△ABC≌△A’B’C’(ASA)
例1:如图,点D 在AB上,点E 在AC上,BA =AC,∠B =∠C.
求证:AD =AE.
证明:在△ABE 和△ACD 中,
∠B =∠C,
AB =AC ,
∠A =∠A ,
∴△ABE ≌△ACD(ASA).
∴AE =AD.
例2:在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?
分析:能否转化为ASA
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理)
在△ABC和△DEF中
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
两角及一角的对边对应相等的两个三角形全等(AAS)
你能从上题中得到什么结论?
符号语言
证明:在△ABC与△A‘ B’ C ‘中
∠A=∠A’
∠B=∠B’
BC=B C’
∴△ABC≌△A’B’C’(AAS)
三、巩固提升
1.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( ) 对.
A. 2 B. 3 C. 4 D. 5
解析:∵CD⊥AB,BE⊥AC,AO平分∠BAC
∴∠ADO=∠AEO=90°,∠DAO=∠EAO
∵AO=AO∴△ADO≌△AEO(AAS)
∴OD=OE,AD=AE
∵∠DOB=∠EOC,∠ODB=∠OEC=90° ∴△BOD≌△COE(ASA)
∴BD=CE,OB=OC,∠B=∠C
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°
∴△ADC≌△AEB(ASA)
∵AD=AE,BD=CE;∴AB=AC
∵OB=OC,AO=AO∴△ABO≌△ACO(SSS)。所以共有四对全等三角形。
故选C。
2、如图,在下列条件中,不能直接证明△ABD≌△ACD的是( )
A. BD=DC,AB=AC
B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD
D. ∠B=∠C,BD=DC
解:∵AD=AD,
A、当BD=DC,AB=AC时,利用SSS证明△ABD≌△ACD,正确;
B、当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD≌△ACD,正确;
C、当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD≌△ACD,正确;
D、当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD≌△ACD,错误.
故选D.
3. △ABC是等腰三角形,AD、BE 分别是∠A、∠B 的角平分线,△ABD和△BAE 全等吗?试说明理由.
∵ △ABC是等腰三角形
∴ AC=BC ∠A=∠B
又∵ AD、BE 分别是∠A、∠B 的角平分线
∴ ∠BAD=1/2 ∠A
∠ABE= 1/2 ∠B
∴ ∠BAD =∠ABE
BAD =∠ABE
AB为公共边
∠EAB=∠DBA
∴△ABD≌△BAE (ASA)
四、课堂小结
1、三角形全等判定
2、隐含条件的找法公共角或部分共角
3、三角形全等条件应用:
通过证明三角形全等,从而证明相关的边相等或角相等
