2021—2022学年人教版数学八年级上册12.1 全等三角形教学设计
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册12.1 全等三角形教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 147.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 20:24:48 | ||
图片预览

文档简介
《12.1 全等三角形》教学设计
课题:12.1 全等三角形 课型:新授课 课时:第一课时
【教学过程】
情境引入
同学们,几何中把“一模一样”的图形叫做”全等图形“,如果是三角形呢?又该怎么判断是不是全等三角形呢?今天我们将一起来学习——全等三角形!
二、探究
把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗?
重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
对应顶点的字母写在对应的位置上.
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”
能够完全重合的两个三角形叫做全等三角形.
三、练习
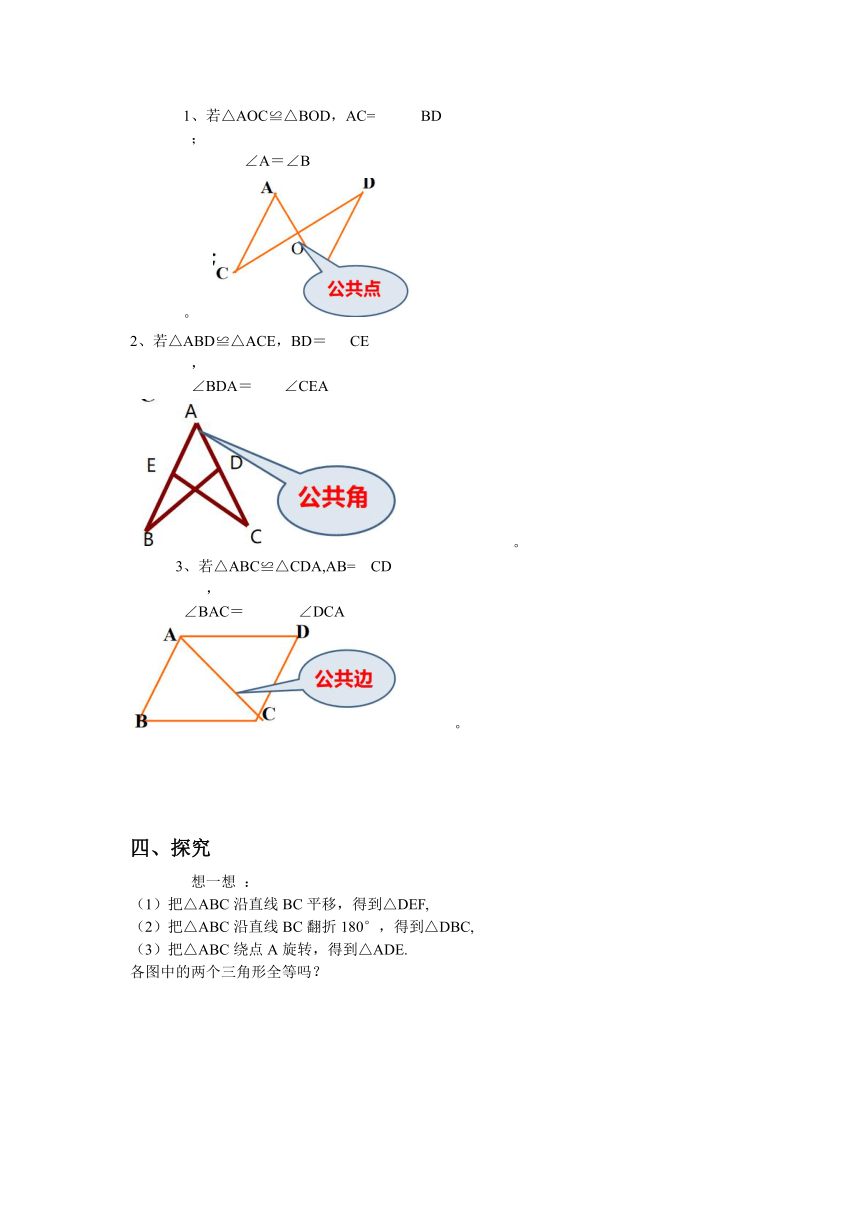
1、若△AOC≌△BOD,AC= BD
;
∠A=∠B
。
2、若△ABD≌△ACE,BD= CE
,
∠BDA= ∠CEA
。
3、若△ABC≌△CDA,AB= CD
,
∠BAC= ∠DCA
。
四、探究
想一想 :
(1)把△ABC沿直线BC平移,得到△DEF,
(2)把△ABC沿直线BC翻折180°,得到△DBC,
(3)把△ABC绕点A旋转,得到△ADE.
各图中的两个三角形全等吗?
平移、翻折、旋转,变换前后的图形全等
练习
已知:如图,△ABC与△DEF是全等三角形,则图中相等的线段的组数是(B )
A.3 B.4 C.5 D.6
解析:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF,
∴BC﹣EC=EF﹣EC,
即BE=CF,有四组相等线段,故选B.
应用提高
如图,△ACB≌△A′CB′,∠ACA′=30°,则∠BCB′的度数为( B )
A.20° B.30°
C.35° D.40°
解析:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∴∠ACB-∠A′CB=∠A′CB′-∠A′CB,
即∠BCB′=∠ACA′,又∠ACA′=30°,
∴∠BCB′=30°,故选:B.
达标测试
1.如图,已知△ABC≌△EDF,下列结论正确的是
( A )
A.∠A=∠E B.∠B=∠DFE
C.AC=ED D.BF=DF
解析: ∵△ABC≌△EDF,
∴∠A=∠E,A正确;
∠B=∠FDE,B错误;
AC=EF,C错误;
BF=DC,D错误;
故选:A.
2.如图,已知ΔABC≌ΔFED, BC=ED, 求证:AB∥EF
证明:
∵ΔABC≌ΔFED, BC=ED ∴BC与ED是对应边
∴∠A=∠F
(全等三角形的对应角相等)
∴AB∥EF
布置作业
教材33页习题12.1第1、2题
课题:12.1 全等三角形 课型:新授课 课时:第一课时
【教学过程】
情境引入
同学们,几何中把“一模一样”的图形叫做”全等图形“,如果是三角形呢?又该怎么判断是不是全等三角形呢?今天我们将一起来学习——全等三角形!
二、探究
把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗?
重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
对应顶点的字母写在对应的位置上.
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”
能够完全重合的两个三角形叫做全等三角形.
三、练习
1、若△AOC≌△BOD,AC= BD
;
∠A=∠B
。
2、若△ABD≌△ACE,BD= CE
,
∠BDA= ∠CEA
。
3、若△ABC≌△CDA,AB= CD
,
∠BAC= ∠DCA
。
四、探究
想一想 :
(1)把△ABC沿直线BC平移,得到△DEF,
(2)把△ABC沿直线BC翻折180°,得到△DBC,
(3)把△ABC绕点A旋转,得到△ADE.
各图中的两个三角形全等吗?
平移、翻折、旋转,变换前后的图形全等
练习
已知:如图,△ABC与△DEF是全等三角形,则图中相等的线段的组数是(B )
A.3 B.4 C.5 D.6
解析:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF,
∴BC﹣EC=EF﹣EC,
即BE=CF,有四组相等线段,故选B.
应用提高
如图,△ACB≌△A′CB′,∠ACA′=30°,则∠BCB′的度数为( B )
A.20° B.30°
C.35° D.40°
解析:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∴∠ACB-∠A′CB=∠A′CB′-∠A′CB,
即∠BCB′=∠ACA′,又∠ACA′=30°,
∴∠BCB′=30°,故选:B.
达标测试
1.如图,已知△ABC≌△EDF,下列结论正确的是
( A )
A.∠A=∠E B.∠B=∠DFE
C.AC=ED D.BF=DF
解析: ∵△ABC≌△EDF,
∴∠A=∠E,A正确;
∠B=∠FDE,B错误;
AC=EF,C错误;
BF=DC,D错误;
故选:A.
2.如图,已知ΔABC≌ΔFED, BC=ED, 求证:AB∥EF
证明:
∵ΔABC≌ΔFED, BC=ED ∴BC与ED是对应边
∴∠A=∠F
(全等三角形的对应角相等)
∴AB∥EF
布置作业
教材33页习题12.1第1、2题
