2021—2022学年人教版数学八年级上册11.3.2多边形的内角和教学设计
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册11.3.2多边形的内角和教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 152.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览

文档简介
《11.3 多边形及其内角和》教学设计
课题:11.3 多边形及其内角和 课型:新授课 课时:第一课时
【教学过程】
导入新课
上堂课,我们一起学习了什么是多边形,以及多边形对角线的相关知识,今天我们将一起来学习多边形以及内角和的知识!
二、知识回顾
1.什么是多边形?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
2.什么是多边形的对角线?
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3.从n边形的一个顶点出发,可以引出_n-3______条对角线,将多边形分割成了_n-2_______个三角形.
三、探究
三角形的内角和等于180°,长方形、正方形的内角和等于__360°
____. 任意四边形的内角和是否也等于360°呢?
证明:连接AC,
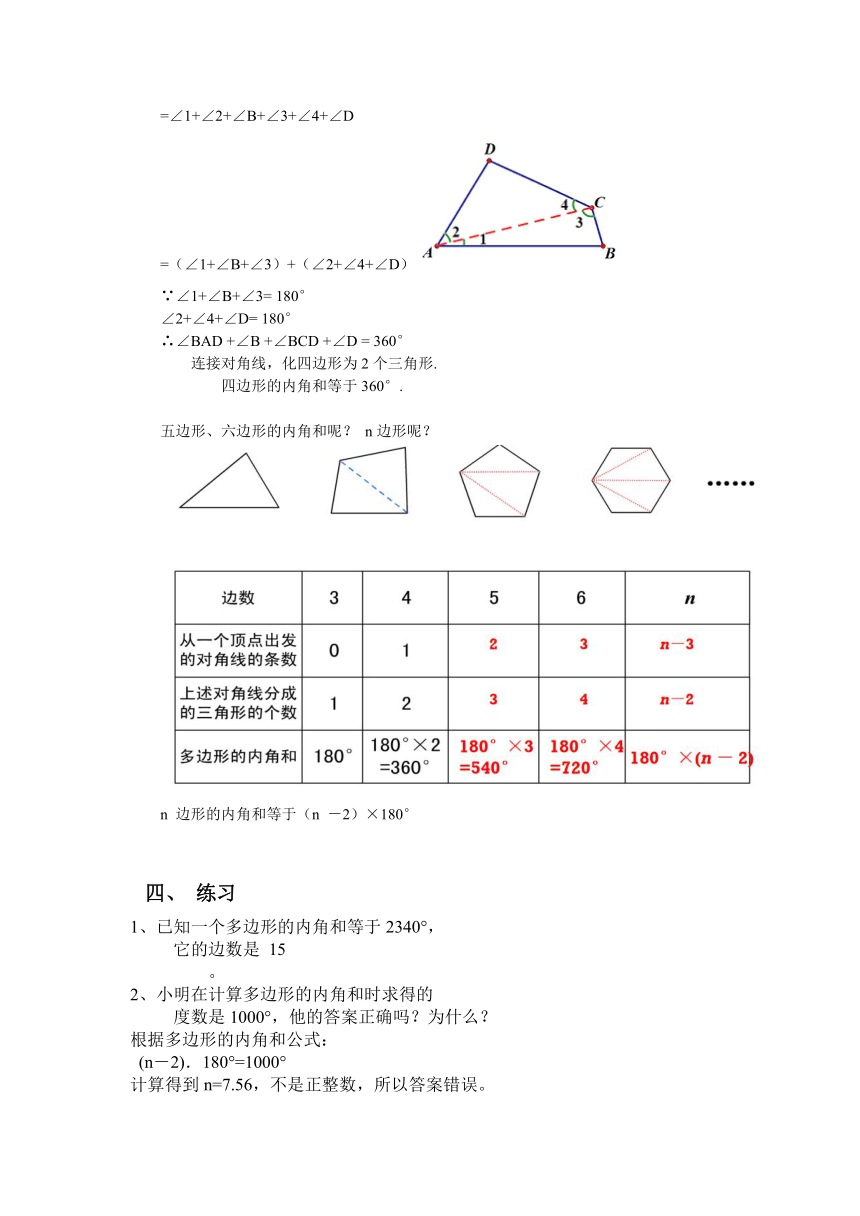
∠BAD +∠B +∠BCD +∠D
=∠1+∠2+∠B+∠3+∠4+∠D
=(∠1+∠B+∠3)+(∠2+∠4+∠D)
∵∠1+∠B+∠3= 180°
∠2+∠4+∠D= 180°
∴∠BAD +∠B +∠BCD +∠D = 360°
连接对角线,化四边形为2个三角形.
四边形的内角和等于360°.
五边形、六边形的内角和呢? n边形呢?
n 边形的内角和等于(n -2)×180°
四、 练习
1、已知一个多边形的内角和等于2340°,
它的边数是 15
。
2、小明在计算多边形的内角和时求得的
度数是1000°,他的答案正确吗?为什么?
根据多边形的内角和公式:
(n-2).180°=1000°
计算得到n=7.56,不是正整数,所以答案错误。
探究
问题:在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.你能求出六边形的外角和吗?
解:∵六边形的任何一个外角加上与它相邻的内角都等于180 °,
∴六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°.
∴六边形外角和=总和-内角和
=6×180°-(6-2)×180°=2×180°=360°
想一想:如果将六边形换为n边形呢?(n是不小于3的任意整数)
n×180°-(n-2)×180°
=2×180°
=360°
多边形的外角和等于360°
应用提高
1.我区某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°,”乙说:“多边形的边数每增加1,则外角和增加180°”,丙说:“多边形的内角和不小于其外角和”,丁说:“只要是多边形,不管有几边,其外角和都是360°”.你认为正确的是(A )
A.甲和丁 B.乙和丙 C.丙和丁 D.以上都不对
解析:根据多边形内角和公式:(n-2) 180 (n≥3)且n为整数)可得甲说:“多边形的边数每增加1,则内角和增加180”是正确的;
根据多边形的外角和定理:多边形的外角和等于360度可知乙说:“多边形的边数每增加1,则外角和增加180°”是错误的;
丙说:“多边形的内角和不小于其外角和”错误,三角形的内角和为180°,外角和为360°,故丙错误;
根据多边形的外角和定理:多边形的外角和等于360度可知丁说:“只要是多边形,不管有几边,其外角和都是360°”正确;
故正确的是:甲和丁,
故选:A
2.如果多边形的内角和等于外角和,则这个多边形的边数是4;如果多边形的内角和等于外角和的2倍,则这个多边形的边数是6;如果多边形的内角和等于外角和的3倍,则这个多边形的边数是8;…;如果多边形的内角和等于外角和的n倍,则这个多边形的边数是 2n+2 .(n为正整数,用n表示)
解析:如果多边形的内角和等于外角和,则这个多边形的边数是2×1+2=4;
如果多边形的内角和等于外角和的2倍,则这个多边形的边数是2×2+2=6;
如果多边形的内角和等于外角和的3倍,则这个多边形的边数是2×3+2=8;…;
如果多边形的内角和等于外角和的n倍,则这个多边形的边数是2n+2,
故答案为:2n+2.
体验收获
今天我们学习了哪些知识?
1.说一说多边形内角和公式?
2.在探究多边形内角和公式中,连接对角线起到什么作用?
3.多边形的外角和等于多少?
八、达标测评
3、 一个多边形当边数增加1时,它的内角和增加多少度?
解: 设多边形的边数为n,
因为它的内角和等于 (n-2) 180°,
当边数增加1时,内角和为(n+1-2) 180°,
(n+1-2) 180°- (n-2) 180°
=n 180°-180°- n 180°+360°
= 180° 内角和增加180°
4、 一个多边形除一个内角外其余各内角和1999°,求这个多边形的变数。
解:设边数为N,这个内角的度数为X.
∴180(n-2)-x=1999,x=180(n-2)-1999
得到x=180n-2359
又∵0∴13 19/180 九、布置作业
教材25页习题11.3第5、6题.
课题:11.3 多边形及其内角和 课型:新授课 课时:第一课时
【教学过程】
导入新课
上堂课,我们一起学习了什么是多边形,以及多边形对角线的相关知识,今天我们将一起来学习多边形以及内角和的知识!
二、知识回顾
1.什么是多边形?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
2.什么是多边形的对角线?
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3.从n边形的一个顶点出发,可以引出_n-3______条对角线,将多边形分割成了_n-2_______个三角形.
三、探究
三角形的内角和等于180°,长方形、正方形的内角和等于__360°
____. 任意四边形的内角和是否也等于360°呢?
证明:连接AC,
∠BAD +∠B +∠BCD +∠D
=∠1+∠2+∠B+∠3+∠4+∠D
=(∠1+∠B+∠3)+(∠2+∠4+∠D)
∵∠1+∠B+∠3= 180°
∠2+∠4+∠D= 180°
∴∠BAD +∠B +∠BCD +∠D = 360°
连接对角线,化四边形为2个三角形.
四边形的内角和等于360°.
五边形、六边形的内角和呢? n边形呢?
n 边形的内角和等于(n -2)×180°
四、 练习
1、已知一个多边形的内角和等于2340°,
它的边数是 15
。
2、小明在计算多边形的内角和时求得的
度数是1000°,他的答案正确吗?为什么?
根据多边形的内角和公式:
(n-2).180°=1000°
计算得到n=7.56,不是正整数,所以答案错误。
探究
问题:在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.你能求出六边形的外角和吗?
解:∵六边形的任何一个外角加上与它相邻的内角都等于180 °,
∴六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°.
∴六边形外角和=总和-内角和
=6×180°-(6-2)×180°=2×180°=360°
想一想:如果将六边形换为n边形呢?(n是不小于3的任意整数)
n×180°-(n-2)×180°
=2×180°
=360°
多边形的外角和等于360°
应用提高
1.我区某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°,”乙说:“多边形的边数每增加1,则外角和增加180°”,丙说:“多边形的内角和不小于其外角和”,丁说:“只要是多边形,不管有几边,其外角和都是360°”.你认为正确的是(A )
A.甲和丁 B.乙和丙 C.丙和丁 D.以上都不对
解析:根据多边形内角和公式:(n-2) 180 (n≥3)且n为整数)可得甲说:“多边形的边数每增加1,则内角和增加180”是正确的;
根据多边形的外角和定理:多边形的外角和等于360度可知乙说:“多边形的边数每增加1,则外角和增加180°”是错误的;
丙说:“多边形的内角和不小于其外角和”错误,三角形的内角和为180°,外角和为360°,故丙错误;
根据多边形的外角和定理:多边形的外角和等于360度可知丁说:“只要是多边形,不管有几边,其外角和都是360°”正确;
故正确的是:甲和丁,
故选:A
2.如果多边形的内角和等于外角和,则这个多边形的边数是4;如果多边形的内角和等于外角和的2倍,则这个多边形的边数是6;如果多边形的内角和等于外角和的3倍,则这个多边形的边数是8;…;如果多边形的内角和等于外角和的n倍,则这个多边形的边数是 2n+2 .(n为正整数,用n表示)
解析:如果多边形的内角和等于外角和,则这个多边形的边数是2×1+2=4;
如果多边形的内角和等于外角和的2倍,则这个多边形的边数是2×2+2=6;
如果多边形的内角和等于外角和的3倍,则这个多边形的边数是2×3+2=8;…;
如果多边形的内角和等于外角和的n倍,则这个多边形的边数是2n+2,
故答案为:2n+2.
体验收获
今天我们学习了哪些知识?
1.说一说多边形内角和公式?
2.在探究多边形内角和公式中,连接对角线起到什么作用?
3.多边形的外角和等于多少?
八、达标测评
3、 一个多边形当边数增加1时,它的内角和增加多少度?
解: 设多边形的边数为n,
因为它的内角和等于 (n-2) 180°,
当边数增加1时,内角和为(n+1-2) 180°,
(n+1-2) 180°- (n-2) 180°
=n 180°-180°- n 180°+360°
= 180° 内角和增加180°
4、 一个多边形除一个内角外其余各内角和1999°,求这个多边形的变数。
解:设边数为N,这个内角的度数为X.
∴180(n-2)-x=1999,x=180(n-2)-1999
得到x=180n-2359
又∵0
教材25页习题11.3第5、6题.
