北师大版六年级数学上册第七章《百分数的应用》知识讲解及考前预测卷精讲(第三套)课件版(41张PPT)
文档属性
| 名称 | 北师大版六年级数学上册第七章《百分数的应用》知识讲解及考前预测卷精讲(第三套)课件版(41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 16:30:47 | ||
图片预览








文档简介
(共41张PPT)
北师大版六年级数学上册第七章
《百分数的应用》知识讲解及考前预测卷精讲
(第三套)
专题复习课件
知识讲解
01
第一部分:知识讲解
(一)百分数的基本概念
1.百分数的定义:表示一个数是另一个数的百分之几的数,叫做百分数。百分数也叫做百分率或百分比。
百分数表示两个数之间的比率关系,不表示具体的数量,所以百分数不能带单位。 2.百分数的意义:表示一个数是另一个数的百分之几。 例如:25%的意义:表示一个数是另一个数的25%。
3.百分数通常不写成分数形式,而在原来分子后面加上“%”来表示。分子部分可为小数、整数,可以大于100,小于100或等于100。 4.小数与百分数互化的规则:
把小数化成百分数,只要把小数点向右移动两位,同时在后面添上百分号; 把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
5.百分数与分数互化的规则:
把分数化成百分数,通常先把分数化成小数(除不尽的保留三位小数),再把小数化成百分数;
把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数。
第一部分:知识讲解
(二)百分数应用题
1、四个公式:
① 谁是谁的几分之几? ② 谁是谁的百分之几?
前面的数是字后面的数 前面的数是字后面的数×100%
③ 谁比谁多百分之几?
④ 谁比谁少百分之几? 比字后面的数-前面的数 比字后面的数 ×100%
比字前面的数-后面的数
比字后面的数×100%
2、两个公式: ① 增加量(减少量)=原来的量×增加的百分数(减少的百分数)
② 现在的量=原来的量±增加量(减少量)
求增加百分之几?减少百分之几?
公式:增加百分之几=增加的部分÷单位1
减少百分之几=减少的部分÷单位1
第一部分:知识讲解
几何形体周长、面积计算公式
1、长方形的周长=(长+宽)×2
2、正方形的周长=边长×4
2、长方形的面积=长×宽
3、正方形的面积=边长×边长
4、 5、三角形的面积=底×高÷2
5、 6、平行四边形的面积=底×高
6、7、梯形的面积=(上底+下底)×高÷2
1、长度单位换算
1千米=1000米 1米=10分米 1分米=10厘米 1米=100厘米 1厘米=10毫米
2、面积单位换算
1平方千米=100公顷 1公顷=10000平方米 1平方米=100平方分米
1平方分米=100平方厘米 1平方厘米=100平方毫米
第一部分:知识讲解
考前押题卷精讲
(全解析)
02
第二部分:学习检测
05
01
02
03
04
填空题
选择题
判断题
计算题
应用题
05
讲解脉络
一.填空题
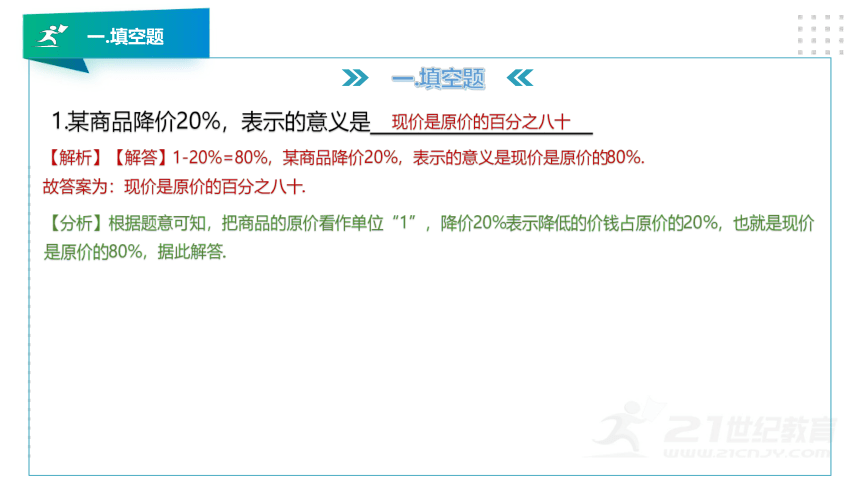
1.某商品降价20%,表示的意义是_______________________
【解析】【解答】1-20%=80%,某商品降价20%,表示的意义是现价是原价的80%.
故答案为:现价是原价的百分之八十.
【分析】根据题意可知,把商品的原价看作单位“1”,降价20%表示降低的价钱占原价的20%,也就是现价是原价的80%,据此解答.
现价是原价的百分之八十
一.填空题
一.填空题
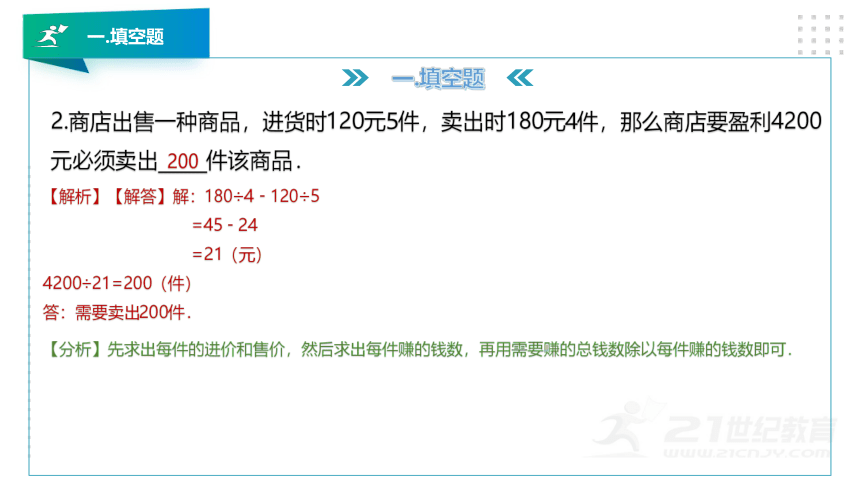
2.商店出售一种商品,进货时120元5件,卖出时180元4件,那么商店要盈利4200元必须卖出_____件该商品.
【解析】【解答】解:180÷4﹣120÷5
=45﹣24
=21(元)
4200÷21=200(件)
答:需要卖出200件.
【分析】先求出每件的进价和售价,然后求出每件赚的钱数,再用需要赚的总钱数除以每件赚的钱数即可.
200
一.填空题
一.填空题
3.______________叫做本金;__________________叫做利息;__________________叫做利率。
【解析】【解答】存入银行的钱叫做本金;取款时银行多付的钱叫做利息;利息占本金的百分比叫做利率。
故答案:存入银行的钱;取款时银行多付的钱;利息占本金的百分比
【分析】本题考查的是本金、利息和利率的基本意义,属于基础知识,要牢固掌握。
存入银行的钱
一.填空题
取款时银行多付的钱
利息占本金的百分比
一.填空题
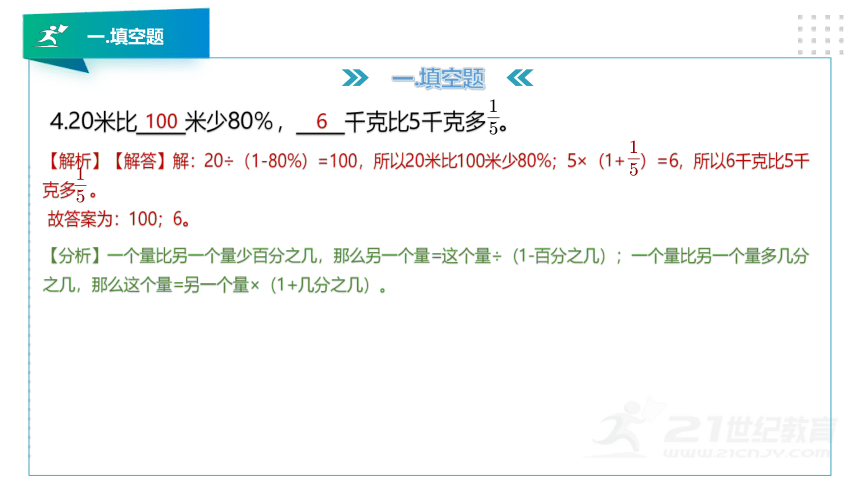
4.20米比_____米少80%,_____千克比5千克多 。
【解析】【解答】解:20÷(1-80%)=100,所以20米比100米少80%;5×(1+ )=6,所以6千克比5千克多 。
故答案为:100;6。
【分析】一个量比另一个量少百分之几,那么另一个量=这个量÷(1-百分之几);一个量比另一个量多几分之几,那么这个量=另一个量×(1+几分之几)。
100
一.填空题
6
一.填空题
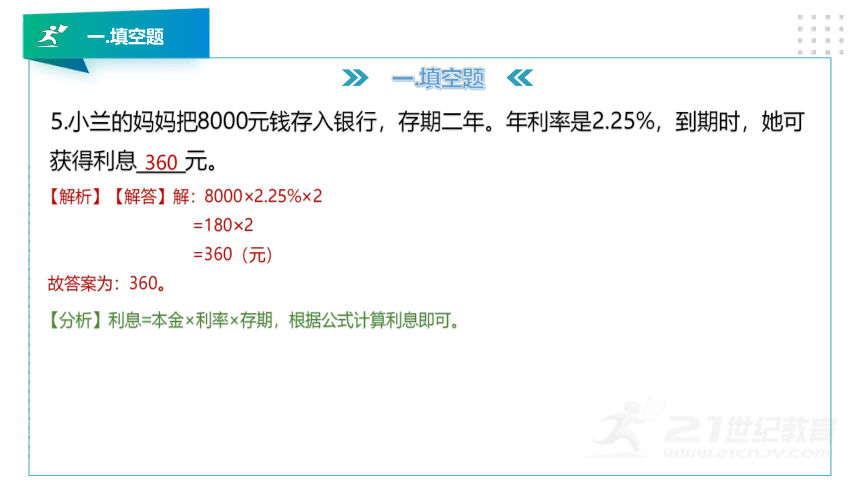
5.小兰的妈妈把8000元钱存入银行,存期二年。年利率是2.25%,到期时,她可获得利息_____元。
【解析】【解答】解:8000×2.25%×2
=180×2
=360(元)
故答案为:360。
【分析】利息=本金×利率×存期,根据公式计算利息即可。
360
一.填空题
一.填空题
6.3cm是5cm的_____%;6kg比5kg多_____%;20m的12%是_____m。
【解析】【解答】3÷5=0.6=60%
(6-5)÷5
=1÷5
=0.2
=20%
20×12%
=20×0.12
=2.4
故答案为:60;20;2.4。
【分析】求一个数是另一个数百分之几,这个数÷另一个数=这个数是另一个数的几分之几,然后将结果化成百分数。
求一个数比另一个数多百分之几,(这个数-另一个数)÷另一个数=这个数比另一个数多几分之几,然后将结果化成百分数。
求一个数的百分之几,这个数×它的百分之几=这个数的百分之几是多少。
60
一.填空题
20
2.4
一.填空题
7.轿车速度比客车快25%,轿车的速度是客车的_____%.
【解析】【解答】解:1×(1+25%)=125%,125%÷1=125%,所以轿车的速度是客车的125%。
故答案为:125。
【分析】将客车的速度看成单位“1”,轿车的速度=客车的速度×(1+轿车速度比客车快百分之几),所以轿车的速度是客车的百分之几=轿车的速度÷客车的速度。
125
一.填空题
一.填空题
8._____吨是42吨的 ,25.2米比18米多_____%。
【解析】【解答】解:42× =7(吨);
(25.2-18)÷18
=7.2÷18
=40%
故答案为:7;40。
【分析】根据分数乘法的意义,用42乘 即可求出42的 是多少。用25.2与18的差除以18即可求出25.2比18多百分之几。
7
一.填空题
40
二.选择题
9.有甲、乙两数,已知(甲数-乙数)÷乙数=60%,这里的60%表示( )。
A. 乙数比甲数少60% B. 甲数比乙数多60% C. 甲数是乙数的60%
【解析】【解答】从甲数-乙数可以看出,甲数大乙数小,表示甲数比乙数多的数或乙数比甲数少的数,从÷乙数可以看出求的是甲数比乙数多。
故答案为:B
【分析】除以哪个数,就是和哪个数作比较,也可以理解为比后面的数就是列式中的除数。
B
二.选择题
二.选择题
10.某工程计划造价80万元,实际造价节省了2.4万元.实际造价节省了百分之几?正确的解答是( )
A. 0.3% B. 30% C. 3% D. 5%
【解析】【解答】解:2.4÷80=3%
故答案为:C
【分析】求实际造价节省了百分之几就是求节省的钱数占计划造价的百分之几,用除法计算即可.
C
二.选择题
二.选择题
11.工厂计划生产一批零件,实际生产的比计划多20%。实际生产的零件数是计划的( ).
A. 1+20% B. 1-20% C. 1×20% D. 1÷20%
【解析】【解答】设计划生产的零件为单位“1”,实际生产的比计划多20%,实际生产的零件数是计划的(1+20%)÷1=1+20%。
故答案为:A。
【分析】把设计划生产的个数看做单位“1”,实际生产的比计划多20%,用实际生产的零件数除以计划生产的零件数,得出答案1+20%。
A
二.选择题
二.选择题
12.甲数是30,甲数比乙数多25%,乙数是( )。
A. 24 B. 25 C. 26 D. 27
【解析】【解答】解:30÷(1+25%)
=30÷125%
=24
故答案为:A。
【分析】乙数为单位“1”,甲数是乙数的(1+25%),根据分数除法的意义,用甲数除以甲数是乙数的百分率即可求出乙数。
A
二.选择题
二.选择题
13.王老师把3000元存入银行,定期2年,年利率按2.5%计算,到期可得本金和税后利息共( )元.
A. 3000 B. 3142.5 C. 150 D. 3150
【解析】【解答】3000×2.5%×2
=75×2
=150(元)
150×(1﹣5%)
=150×95%
=142.5(元)
3000+142.5=3142.5(元)
答:到期可得本金和税后利息共3142.5元。
故答案为:B
【分析】利息=本金×年利率×时间,由此代入数据求出利息;再把这个利息看成单位“1”,实得利息是总利息的1﹣5%;最后拿到的钱是缴纳利息税后的实得利息+本金,由此解决问题。
B
二.选择题
二.选择题
14.乙数比甲数少40%,甲数和乙数的比是( )
A. 2:3 B. 3:2 C. 3:5 D. 5:3
【解析】【解答】解:乙数=甲数×(1-40%)=60%×甲数,所以甲数:乙数=甲数:60%甲数=5:3。
故答案为:D。
【分析】一个数比另一个数少百分之几,那么这个数=另一个数×(1-百分之几十),然后将甲、乙两数作比即可。
D
二.选择题
二.选择题
15.加工一批零件,王师傅要用10小时,李师傅要用8小时,那么王师傅的工作效率比李师傅的工作效率低( )。
A. 20% B. 25% C. 120% D. 125%
【解析】【解答】解:
=20%
故答案为:A。
【分析】把这批零件看作单位“1”,用分数分别表示出两人的工作效率,然后用两人的工作效率差除以李师傅的工作效率即可求出王师傅的工作效率比李师傅的工作效率低百分之几。
A
二.选择题
二.选择题
16.六(2)班有男生25人,比女生多5人,男生人数比女生人数多百分之几?正确的列式是( )
A. (25﹣5)÷25 B. 5÷(25+5) C. 5÷(25﹣5)
【解析】【解答】解:5÷(25﹣5)
=5÷20
=25%
答:男生人数比女生人数多25%.
故选:C.
【分析】男生比女生多5人,先用男生的人数减去5人,求出女生的人数,再用多的人数除以女生的人数即可.
C
二.选择题
三.判断题
17.利息一定小于本金。 ( )
【解析】【解答】利息的多少与利率和存款的时间有关,当时间一定长时,利息可能大于本金。
故答案为:×
【分析】考查了学生对利息意义的掌握情况,利息=本金×利率×时间,当时间与利率的乘积大于1时,利息就要大于本金。
×
三.判断题
三.判断题
18.存款的利息按20%的税率纳税。( )
【解析】【解答】存款的利息纳税税率是按当时银行的规定纳税。
故答案为:×
【分析】存款的利息纳税税率是按当时银行的规定纳税,比如说现在的存款,就不纳利息税。关键是,存款的利息根据当时银行的规定纳税。
×
三.判断题
三.判断题
19.利息等于本金乘以时间乘以利率。 ( )
【解析】【解答】解:利息等于本金乘以时间乘以利率,原题说法正确.
故答案为:√
【分析】利息=本金×利率×时间,由此根据利息的计算公式判断即可.
√
三.判断题
三.判断题
20.科技书比文艺书多25%,那么文艺书就比科技书少20%。 ( )
【解析】【解答】将文艺书看成单位:“1”,科技书有(1+25%),
[(1+25%)-1]÷(1+25%)×100%
=(1.25-1)÷1.25×100%
=0.25÷1.25×100%
=0.2×100%
=20%
故答案为:√
【分析】科技书的本数=文艺书的本数×(1+25%),文艺书比科技书少百分之几=(科技书的本数-文艺书的本数)÷科技书的本数×100%,据此进行计算即可。
√
三.判断题
三.判断题
21.一种商品先提价10%,然后又降价10%,结果与原价相等。 ( )
【解析】【解答】假设这件商品的原价是“1”,
现价是:1×(1+10%)×(1-10%)
=1×1.1×0.9
=0.99
0.99<1,现价比原价少,原题说法错误.
故答案为:×
【分析】根据题意可知,假设这件商品的原价是“1”,求出先提价10%后的价格,然后把提价后的价钱看作新的单位“1”,然后再降低10%,求出现在的价格,最后用现价与原价对比即可.
×
三.判断题
四.计算题
22.看图列式计算。
(1) (2)
【答案】 (1)解:20×(1+10%)=22(人)
(2)解:36÷(1-25%)=48(只)
【解析】【分析】(1)女生的人数=男生的人数×(1+女生比男生多百分之几),锯成列式作答即可;
(2)白兔的只数=黑兔的只数÷(1-黑兔比白兔少百分之几),锯成列式作答即可。
四.计算题
五.应用题
23.下图是电脑城2015年1月~5月甲、乙两种品牌电脑的销售情况统计图。
(1)2015年1月份乙品牌电脑比甲品牌电脑少售出百分之几?4月份甲品牌电脑比乙品牌电脑多售出百分之几?
(2)请你完成下面的统计图。
【答案】 (1)解:(80-40)÷80=40÷80=50%
(45-25)÷25=20÷25=80%
答:2015年1月份乙品牌电脑比甲品牌电脑少售出50%,4月份甲品牌电脑比乙品牌电脑多售出80%.
(2)解:根据条形统计图的数据,绘制折线统计如图:
五.应用题
五.应用题
【解析】【分析】(1)要求2015年1月份乙品牌电脑比甲品牌电脑少售出百分之几,用(甲品牌电脑的台数-乙品牌电脑的台数)÷甲品牌的电脑台数=2015年1月份乙品牌电脑比甲品牌电脑少售出百分之几;要求4月份甲品牌电脑比乙品牌电脑多售出百分之几,用(甲品牌电脑的台数-乙品牌电脑的台数)÷乙品牌的电脑台数=2015年4月份甲品牌电脑比乙品牌电脑多售出百分之几,据此列式计算;(2)根据条形统计图中的数据,根据数量的多少先描出各点,再把各点用线段顺次连接起来,据此绘制折线统计图即可.
五.应用题
五.应用题
24.某公司去年的产值是4500万元,今年的产值比去年增长10%。
(1)该公司今年的产值比去年增长多少万元?
(2)该公司今年的产值是多少万元?
【答案】 (1)解:4500×10%=450(万元)
答: 该公司今年的产值比去年增长450万元。
(2)解:4500+450=4950(万元)
答: 该公司今年的产值是4950万元。
【解析】【分析】(1)根据条件“ 某公司去年的产值是4500万元,今年的产值比去年增长10% ”可知,去年的产值×10%=今年比去年增长的产值,据此列式计算;
(2)根据题意可知,去年的产值+今年比去年增长的产值=今年的产值,据此列式解答。
五.应用题
五.应用题
25.李叔叔购买了五年期的国家建设债券20000元,年利率是3.81%。到期时,李叔叔应得到利息多少元
【答案】 解:20000× 3.81% ×5
=762×5
=3810(元)
答:李叔叔应得到利息3810元。
【解析】【分析】根据题意可知利息=本金×利率×时间即可。
五.应用题
五.应用题
26.张经理向商店订购某种商品80件,每件定价100元.张先生向商店经理说:“如果你肯减价,每减价1元,我就多订购4件.”商店经理算了一下,如果减价5%,那么由于张先生多订购,仍可获得与原来一样多的利润.问:这种商品的成本是多少元?
【答案】 解:80×100=8000(元)
100×(1-5%)=95(元)
100×5%×4=20(件)
(80+20)×95=9500(元)
(9500-8000)÷20=75(元)
答:这种商品的成本是75元。
【解析】【分析】降价之前,张先生订购这种商品需要支付的钱数=订购的件数×每件的定价,减价5%后每件商品的价钱=每件的定价×(1-5%),那么减价5%后多订购的件数=每件的定价×5%×减价1元多订的件数,那么减价5%后张先生需要支付的钱数=(原来订购的件数+减价5%后多订购的件数)×减价5%后每件商品的价钱,那么每件的成本=降价之后与降价之前支付的钱数之差÷减价5%后多订购的件数。
五.应用题
五.应用题
27.一杯调制后的奶茶,其中的糖分和其余成分的比是1:9,现要配制 600g奶茶,需要多少克的糖 《中国居民膳食指南(2016)》建议:每天糖的摄入量最好控制在25g以下。这杯奶茶的含糖量超过了建议控制糖量的百分之几
【答案】解:600÷(1+9)×1=60(克)
(60-25)÷25=140%
答:配制600g奶茶,需要60克的糖;这杯奶茶的含糖量超过了建议控制糖量的140%。
【解析】【分析】配制600g奶茶,需要糖的质量=600÷糖分和其余成分占的份数和×糖分占的份数;这杯奶茶的含糖量超过了建议控制糖量的百分之几=(奶茶的含糖量-每天糖的摄入量)÷每天糖的摄入量,据此代入数值作答即可。
五.应用题
五.应用题
28.苏宁电器清仓处理部分电脑,每台售价3000元,亏本20%,每台电脑的原价是多少元?
【答案】 解:设每台电脑的原价是x元。
x-20%x=3000
0.8x=3000
x=3750
答:每台电脑的原价是3750元。
【解析】【分析】等量关系:电脑的原价-亏本的价钱(原价×20%)=电脑的售价3000元,根据等量关系列方程,根据等式性质2解方程。
五.应用题
五.应用题
29.今年猪肉价格涨得特别快,全国生猪价格8月份第一周比前一周上涨5%,第二周比第一周又上涨6%。8月份前两周生猪价格上涨了百分之几
【答案】 解:1×(1+5%)×(1+6%)
=1×1.05×1.06
=1.113
(1.113-1)÷1=11.3%
答:8月份前两周生猪价格上涨了11.3%。
【解析】【分析】把前一周的价格看作1,则第一周价格是前一周价格的(1+5%),第二周价格是第一周价格的(1+6%),根据分数乘法的意义求出第二周的价格;然后用第二周的价格减去前一周的价格再除以前一周的价格即可求出前两周价格上涨了百分之几。
五.应用题
五.应用题
30.一种电脑销售中第一次比原价3600元降低了10%,第二次又降低了10%。这种电脑现价多少元钱?
【答案】 解:3600×10%=360(元)
3600-360=3240(元)
3240×10%=324(元)
3240-324=2916(元)
答:这种电脑现价2916元。
【解析】【分析】第一次降低了10%是降低了原价的10%,所以可以先用乘法计算出来第一次降低了多少钱,进一步用减法计算出第一次降价后的价钱。然后第二次又降低了10%是降低了第一次降价后价钱的10%而不是原价,所以用第一次降价后价钱再乘以10%可以计算出第二次降低了多少钱,进一步用第一次降价后价钱减去第二次降低的价钱得到第二次降价后的价钱也就是现价。
五.应用题
谢谢您的观看!
https://www.21cnjy.com/help/help_extract.php
北师大版六年级数学上册第七章
《百分数的应用》知识讲解及考前预测卷精讲
(第三套)
专题复习课件
知识讲解
01
第一部分:知识讲解
(一)百分数的基本概念
1.百分数的定义:表示一个数是另一个数的百分之几的数,叫做百分数。百分数也叫做百分率或百分比。
百分数表示两个数之间的比率关系,不表示具体的数量,所以百分数不能带单位。 2.百分数的意义:表示一个数是另一个数的百分之几。 例如:25%的意义:表示一个数是另一个数的25%。
3.百分数通常不写成分数形式,而在原来分子后面加上“%”来表示。分子部分可为小数、整数,可以大于100,小于100或等于100。 4.小数与百分数互化的规则:
把小数化成百分数,只要把小数点向右移动两位,同时在后面添上百分号; 把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
5.百分数与分数互化的规则:
把分数化成百分数,通常先把分数化成小数(除不尽的保留三位小数),再把小数化成百分数;
把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数。
第一部分:知识讲解
(二)百分数应用题
1、四个公式:
① 谁是谁的几分之几? ② 谁是谁的百分之几?
前面的数是字后面的数 前面的数是字后面的数×100%
③ 谁比谁多百分之几?
④ 谁比谁少百分之几? 比字后面的数-前面的数 比字后面的数 ×100%
比字前面的数-后面的数
比字后面的数×100%
2、两个公式: ① 增加量(减少量)=原来的量×增加的百分数(减少的百分数)
② 现在的量=原来的量±增加量(减少量)
求增加百分之几?减少百分之几?
公式:增加百分之几=增加的部分÷单位1
减少百分之几=减少的部分÷单位1
第一部分:知识讲解
几何形体周长、面积计算公式
1、长方形的周长=(长+宽)×2
2、正方形的周长=边长×4
2、长方形的面积=长×宽
3、正方形的面积=边长×边长
4、 5、三角形的面积=底×高÷2
5、 6、平行四边形的面积=底×高
6、7、梯形的面积=(上底+下底)×高÷2
1、长度单位换算
1千米=1000米 1米=10分米 1分米=10厘米 1米=100厘米 1厘米=10毫米
2、面积单位换算
1平方千米=100公顷 1公顷=10000平方米 1平方米=100平方分米
1平方分米=100平方厘米 1平方厘米=100平方毫米
第一部分:知识讲解
考前押题卷精讲
(全解析)
02
第二部分:学习检测
05
01
02
03
04
填空题
选择题
判断题
计算题
应用题
05
讲解脉络
一.填空题
1.某商品降价20%,表示的意义是_______________________
【解析】【解答】1-20%=80%,某商品降价20%,表示的意义是现价是原价的80%.
故答案为:现价是原价的百分之八十.
【分析】根据题意可知,把商品的原价看作单位“1”,降价20%表示降低的价钱占原价的20%,也就是现价是原价的80%,据此解答.
现价是原价的百分之八十
一.填空题
一.填空题
2.商店出售一种商品,进货时120元5件,卖出时180元4件,那么商店要盈利4200元必须卖出_____件该商品.
【解析】【解答】解:180÷4﹣120÷5
=45﹣24
=21(元)
4200÷21=200(件)
答:需要卖出200件.
【分析】先求出每件的进价和售价,然后求出每件赚的钱数,再用需要赚的总钱数除以每件赚的钱数即可.
200
一.填空题
一.填空题
3.______________叫做本金;__________________叫做利息;__________________叫做利率。
【解析】【解答】存入银行的钱叫做本金;取款时银行多付的钱叫做利息;利息占本金的百分比叫做利率。
故答案:存入银行的钱;取款时银行多付的钱;利息占本金的百分比
【分析】本题考查的是本金、利息和利率的基本意义,属于基础知识,要牢固掌握。
存入银行的钱
一.填空题
取款时银行多付的钱
利息占本金的百分比
一.填空题
4.20米比_____米少80%,_____千克比5千克多 。
【解析】【解答】解:20÷(1-80%)=100,所以20米比100米少80%;5×(1+ )=6,所以6千克比5千克多 。
故答案为:100;6。
【分析】一个量比另一个量少百分之几,那么另一个量=这个量÷(1-百分之几);一个量比另一个量多几分之几,那么这个量=另一个量×(1+几分之几)。
100
一.填空题
6
一.填空题
5.小兰的妈妈把8000元钱存入银行,存期二年。年利率是2.25%,到期时,她可获得利息_____元。
【解析】【解答】解:8000×2.25%×2
=180×2
=360(元)
故答案为:360。
【分析】利息=本金×利率×存期,根据公式计算利息即可。
360
一.填空题
一.填空题
6.3cm是5cm的_____%;6kg比5kg多_____%;20m的12%是_____m。
【解析】【解答】3÷5=0.6=60%
(6-5)÷5
=1÷5
=0.2
=20%
20×12%
=20×0.12
=2.4
故答案为:60;20;2.4。
【分析】求一个数是另一个数百分之几,这个数÷另一个数=这个数是另一个数的几分之几,然后将结果化成百分数。
求一个数比另一个数多百分之几,(这个数-另一个数)÷另一个数=这个数比另一个数多几分之几,然后将结果化成百分数。
求一个数的百分之几,这个数×它的百分之几=这个数的百分之几是多少。
60
一.填空题
20
2.4
一.填空题
7.轿车速度比客车快25%,轿车的速度是客车的_____%.
【解析】【解答】解:1×(1+25%)=125%,125%÷1=125%,所以轿车的速度是客车的125%。
故答案为:125。
【分析】将客车的速度看成单位“1”,轿车的速度=客车的速度×(1+轿车速度比客车快百分之几),所以轿车的速度是客车的百分之几=轿车的速度÷客车的速度。
125
一.填空题
一.填空题
8._____吨是42吨的 ,25.2米比18米多_____%。
【解析】【解答】解:42× =7(吨);
(25.2-18)÷18
=7.2÷18
=40%
故答案为:7;40。
【分析】根据分数乘法的意义,用42乘 即可求出42的 是多少。用25.2与18的差除以18即可求出25.2比18多百分之几。
7
一.填空题
40
二.选择题
9.有甲、乙两数,已知(甲数-乙数)÷乙数=60%,这里的60%表示( )。
A. 乙数比甲数少60% B. 甲数比乙数多60% C. 甲数是乙数的60%
【解析】【解答】从甲数-乙数可以看出,甲数大乙数小,表示甲数比乙数多的数或乙数比甲数少的数,从÷乙数可以看出求的是甲数比乙数多。
故答案为:B
【分析】除以哪个数,就是和哪个数作比较,也可以理解为比后面的数就是列式中的除数。
B
二.选择题
二.选择题
10.某工程计划造价80万元,实际造价节省了2.4万元.实际造价节省了百分之几?正确的解答是( )
A. 0.3% B. 30% C. 3% D. 5%
【解析】【解答】解:2.4÷80=3%
故答案为:C
【分析】求实际造价节省了百分之几就是求节省的钱数占计划造价的百分之几,用除法计算即可.
C
二.选择题
二.选择题
11.工厂计划生产一批零件,实际生产的比计划多20%。实际生产的零件数是计划的( ).
A. 1+20% B. 1-20% C. 1×20% D. 1÷20%
【解析】【解答】设计划生产的零件为单位“1”,实际生产的比计划多20%,实际生产的零件数是计划的(1+20%)÷1=1+20%。
故答案为:A。
【分析】把设计划生产的个数看做单位“1”,实际生产的比计划多20%,用实际生产的零件数除以计划生产的零件数,得出答案1+20%。
A
二.选择题
二.选择题
12.甲数是30,甲数比乙数多25%,乙数是( )。
A. 24 B. 25 C. 26 D. 27
【解析】【解答】解:30÷(1+25%)
=30÷125%
=24
故答案为:A。
【分析】乙数为单位“1”,甲数是乙数的(1+25%),根据分数除法的意义,用甲数除以甲数是乙数的百分率即可求出乙数。
A
二.选择题
二.选择题
13.王老师把3000元存入银行,定期2年,年利率按2.5%计算,到期可得本金和税后利息共( )元.
A. 3000 B. 3142.5 C. 150 D. 3150
【解析】【解答】3000×2.5%×2
=75×2
=150(元)
150×(1﹣5%)
=150×95%
=142.5(元)
3000+142.5=3142.5(元)
答:到期可得本金和税后利息共3142.5元。
故答案为:B
【分析】利息=本金×年利率×时间,由此代入数据求出利息;再把这个利息看成单位“1”,实得利息是总利息的1﹣5%;最后拿到的钱是缴纳利息税后的实得利息+本金,由此解决问题。
B
二.选择题
二.选择题
14.乙数比甲数少40%,甲数和乙数的比是( )
A. 2:3 B. 3:2 C. 3:5 D. 5:3
【解析】【解答】解:乙数=甲数×(1-40%)=60%×甲数,所以甲数:乙数=甲数:60%甲数=5:3。
故答案为:D。
【分析】一个数比另一个数少百分之几,那么这个数=另一个数×(1-百分之几十),然后将甲、乙两数作比即可。
D
二.选择题
二.选择题
15.加工一批零件,王师傅要用10小时,李师傅要用8小时,那么王师傅的工作效率比李师傅的工作效率低( )。
A. 20% B. 25% C. 120% D. 125%
【解析】【解答】解:
=20%
故答案为:A。
【分析】把这批零件看作单位“1”,用分数分别表示出两人的工作效率,然后用两人的工作效率差除以李师傅的工作效率即可求出王师傅的工作效率比李师傅的工作效率低百分之几。
A
二.选择题
二.选择题
16.六(2)班有男生25人,比女生多5人,男生人数比女生人数多百分之几?正确的列式是( )
A. (25﹣5)÷25 B. 5÷(25+5) C. 5÷(25﹣5)
【解析】【解答】解:5÷(25﹣5)
=5÷20
=25%
答:男生人数比女生人数多25%.
故选:C.
【分析】男生比女生多5人,先用男生的人数减去5人,求出女生的人数,再用多的人数除以女生的人数即可.
C
二.选择题
三.判断题
17.利息一定小于本金。 ( )
【解析】【解答】利息的多少与利率和存款的时间有关,当时间一定长时,利息可能大于本金。
故答案为:×
【分析】考查了学生对利息意义的掌握情况,利息=本金×利率×时间,当时间与利率的乘积大于1时,利息就要大于本金。
×
三.判断题
三.判断题
18.存款的利息按20%的税率纳税。( )
【解析】【解答】存款的利息纳税税率是按当时银行的规定纳税。
故答案为:×
【分析】存款的利息纳税税率是按当时银行的规定纳税,比如说现在的存款,就不纳利息税。关键是,存款的利息根据当时银行的规定纳税。
×
三.判断题
三.判断题
19.利息等于本金乘以时间乘以利率。 ( )
【解析】【解答】解:利息等于本金乘以时间乘以利率,原题说法正确.
故答案为:√
【分析】利息=本金×利率×时间,由此根据利息的计算公式判断即可.
√
三.判断题
三.判断题
20.科技书比文艺书多25%,那么文艺书就比科技书少20%。 ( )
【解析】【解答】将文艺书看成单位:“1”,科技书有(1+25%),
[(1+25%)-1]÷(1+25%)×100%
=(1.25-1)÷1.25×100%
=0.25÷1.25×100%
=0.2×100%
=20%
故答案为:√
【分析】科技书的本数=文艺书的本数×(1+25%),文艺书比科技书少百分之几=(科技书的本数-文艺书的本数)÷科技书的本数×100%,据此进行计算即可。
√
三.判断题
三.判断题
21.一种商品先提价10%,然后又降价10%,结果与原价相等。 ( )
【解析】【解答】假设这件商品的原价是“1”,
现价是:1×(1+10%)×(1-10%)
=1×1.1×0.9
=0.99
0.99<1,现价比原价少,原题说法错误.
故答案为:×
【分析】根据题意可知,假设这件商品的原价是“1”,求出先提价10%后的价格,然后把提价后的价钱看作新的单位“1”,然后再降低10%,求出现在的价格,最后用现价与原价对比即可.
×
三.判断题
四.计算题
22.看图列式计算。
(1) (2)
【答案】 (1)解:20×(1+10%)=22(人)
(2)解:36÷(1-25%)=48(只)
【解析】【分析】(1)女生的人数=男生的人数×(1+女生比男生多百分之几),锯成列式作答即可;
(2)白兔的只数=黑兔的只数÷(1-黑兔比白兔少百分之几),锯成列式作答即可。
四.计算题
五.应用题
23.下图是电脑城2015年1月~5月甲、乙两种品牌电脑的销售情况统计图。
(1)2015年1月份乙品牌电脑比甲品牌电脑少售出百分之几?4月份甲品牌电脑比乙品牌电脑多售出百分之几?
(2)请你完成下面的统计图。
【答案】 (1)解:(80-40)÷80=40÷80=50%
(45-25)÷25=20÷25=80%
答:2015年1月份乙品牌电脑比甲品牌电脑少售出50%,4月份甲品牌电脑比乙品牌电脑多售出80%.
(2)解:根据条形统计图的数据,绘制折线统计如图:
五.应用题
五.应用题
【解析】【分析】(1)要求2015年1月份乙品牌电脑比甲品牌电脑少售出百分之几,用(甲品牌电脑的台数-乙品牌电脑的台数)÷甲品牌的电脑台数=2015年1月份乙品牌电脑比甲品牌电脑少售出百分之几;要求4月份甲品牌电脑比乙品牌电脑多售出百分之几,用(甲品牌电脑的台数-乙品牌电脑的台数)÷乙品牌的电脑台数=2015年4月份甲品牌电脑比乙品牌电脑多售出百分之几,据此列式计算;(2)根据条形统计图中的数据,根据数量的多少先描出各点,再把各点用线段顺次连接起来,据此绘制折线统计图即可.
五.应用题
五.应用题
24.某公司去年的产值是4500万元,今年的产值比去年增长10%。
(1)该公司今年的产值比去年增长多少万元?
(2)该公司今年的产值是多少万元?
【答案】 (1)解:4500×10%=450(万元)
答: 该公司今年的产值比去年增长450万元。
(2)解:4500+450=4950(万元)
答: 该公司今年的产值是4950万元。
【解析】【分析】(1)根据条件“ 某公司去年的产值是4500万元,今年的产值比去年增长10% ”可知,去年的产值×10%=今年比去年增长的产值,据此列式计算;
(2)根据题意可知,去年的产值+今年比去年增长的产值=今年的产值,据此列式解答。
五.应用题
五.应用题
25.李叔叔购买了五年期的国家建设债券20000元,年利率是3.81%。到期时,李叔叔应得到利息多少元
【答案】 解:20000× 3.81% ×5
=762×5
=3810(元)
答:李叔叔应得到利息3810元。
【解析】【分析】根据题意可知利息=本金×利率×时间即可。
五.应用题
五.应用题
26.张经理向商店订购某种商品80件,每件定价100元.张先生向商店经理说:“如果你肯减价,每减价1元,我就多订购4件.”商店经理算了一下,如果减价5%,那么由于张先生多订购,仍可获得与原来一样多的利润.问:这种商品的成本是多少元?
【答案】 解:80×100=8000(元)
100×(1-5%)=95(元)
100×5%×4=20(件)
(80+20)×95=9500(元)
(9500-8000)÷20=75(元)
答:这种商品的成本是75元。
【解析】【分析】降价之前,张先生订购这种商品需要支付的钱数=订购的件数×每件的定价,减价5%后每件商品的价钱=每件的定价×(1-5%),那么减价5%后多订购的件数=每件的定价×5%×减价1元多订的件数,那么减价5%后张先生需要支付的钱数=(原来订购的件数+减价5%后多订购的件数)×减价5%后每件商品的价钱,那么每件的成本=降价之后与降价之前支付的钱数之差÷减价5%后多订购的件数。
五.应用题
五.应用题
27.一杯调制后的奶茶,其中的糖分和其余成分的比是1:9,现要配制 600g奶茶,需要多少克的糖 《中国居民膳食指南(2016)》建议:每天糖的摄入量最好控制在25g以下。这杯奶茶的含糖量超过了建议控制糖量的百分之几
【答案】解:600÷(1+9)×1=60(克)
(60-25)÷25=140%
答:配制600g奶茶,需要60克的糖;这杯奶茶的含糖量超过了建议控制糖量的140%。
【解析】【分析】配制600g奶茶,需要糖的质量=600÷糖分和其余成分占的份数和×糖分占的份数;这杯奶茶的含糖量超过了建议控制糖量的百分之几=(奶茶的含糖量-每天糖的摄入量)÷每天糖的摄入量,据此代入数值作答即可。
五.应用题
五.应用题
28.苏宁电器清仓处理部分电脑,每台售价3000元,亏本20%,每台电脑的原价是多少元?
【答案】 解:设每台电脑的原价是x元。
x-20%x=3000
0.8x=3000
x=3750
答:每台电脑的原价是3750元。
【解析】【分析】等量关系:电脑的原价-亏本的价钱(原价×20%)=电脑的售价3000元,根据等量关系列方程,根据等式性质2解方程。
五.应用题
五.应用题
29.今年猪肉价格涨得特别快,全国生猪价格8月份第一周比前一周上涨5%,第二周比第一周又上涨6%。8月份前两周生猪价格上涨了百分之几
【答案】 解:1×(1+5%)×(1+6%)
=1×1.05×1.06
=1.113
(1.113-1)÷1=11.3%
答:8月份前两周生猪价格上涨了11.3%。
【解析】【分析】把前一周的价格看作1,则第一周价格是前一周价格的(1+5%),第二周价格是第一周价格的(1+6%),根据分数乘法的意义求出第二周的价格;然后用第二周的价格减去前一周的价格再除以前一周的价格即可求出前两周价格上涨了百分之几。
五.应用题
五.应用题
30.一种电脑销售中第一次比原价3600元降低了10%,第二次又降低了10%。这种电脑现价多少元钱?
【答案】 解:3600×10%=360(元)
3600-360=3240(元)
3240×10%=324(元)
3240-324=2916(元)
答:这种电脑现价2916元。
【解析】【分析】第一次降低了10%是降低了原价的10%,所以可以先用乘法计算出来第一次降低了多少钱,进一步用减法计算出第一次降价后的价钱。然后第二次又降低了10%是降低了第一次降价后价钱的10%而不是原价,所以用第一次降价后价钱再乘以10%可以计算出第二次降低了多少钱,进一步用第一次降价后价钱减去第二次降低的价钱得到第二次降价后的价钱也就是现价。
五.应用题
谢谢您的观看!
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
