广西防城港市防城中学2021-2022学年高二上学期期中考试数学试题(word 含答案)
文档属性
| 名称 | 广西防城港市防城中学2021-2022学年高二上学期期中考试数学试题(word 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 509.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 08:55:19 | ||
图片预览

文档简介
高二数学
一、单项选择题:本题共12小题,每小题5分,共60分。
1.已知,,则( )
A.3 B.4 C.5 D.6
2.过两点,的直线方程为( )
A. B.
C. D.
3.直线在轴上的截距为( )
A. B. C.2 D.-2
4.如果空间四点A,B,C,D不共面,那么下列判断中正确的是( )
A.A,B,C,D四点中必有三点共线 B.直线AB与CD相交
C.A,B,C,D四点中不存在三点共线 D.直线AB与CD平行
5.已知直线:,:,则,之间的距离为( )
A.1 B. C. D.2
6.已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.与圆:同圆心,且面积为面积的一半的圆的方程为( )
A. B.
C. D.
8.在下列关于直线l,m和平面,的命题中真命题是( )
A.若且,则 B.若且,则
C.若且,则 D.若且,则
9.某几何体的三视图如图所示,则该几何体的表面积为( )
A. B. C. D.
10.已知直线:与直线:平行,则实数为( )
A.3 B.-2 C.3或-2 D.以上都不对
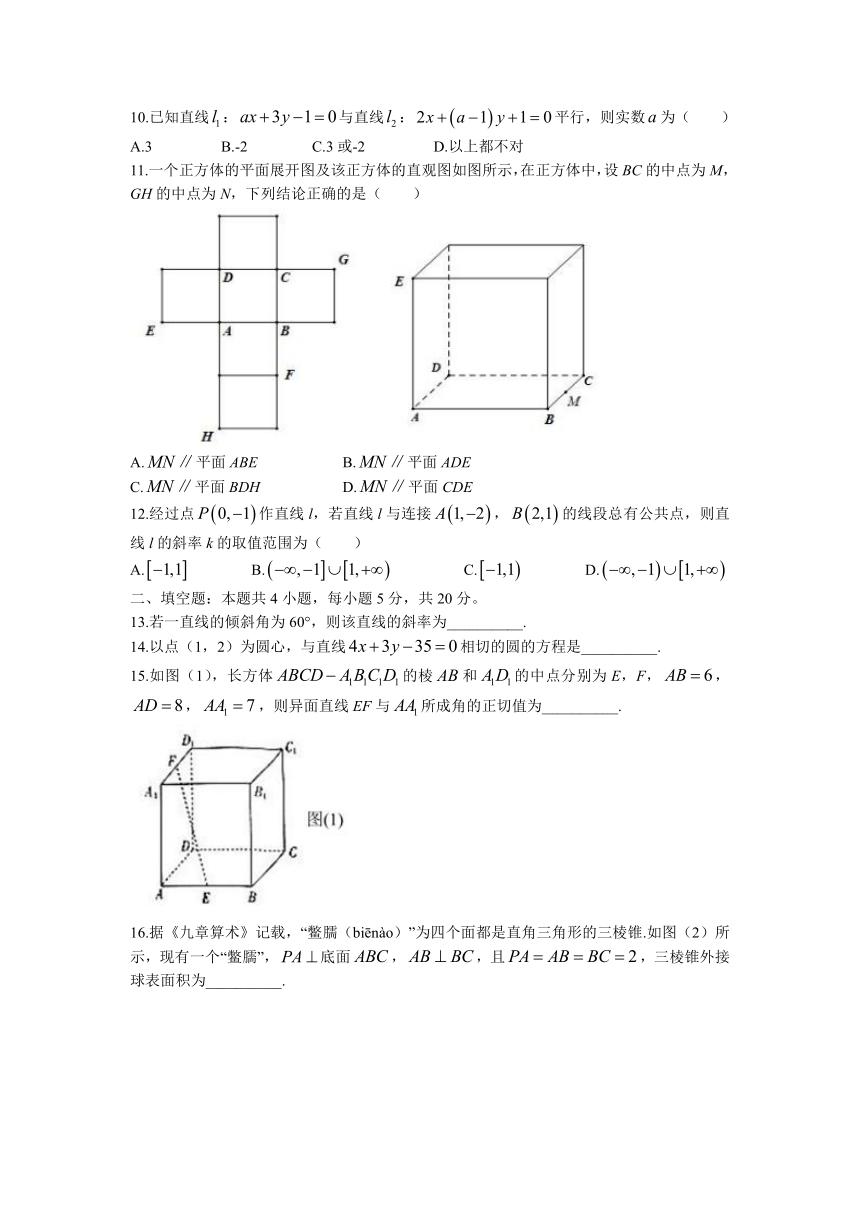
11.一个正方体的平面展开图及该正方体的直观图如图所示,在正方体中,设BC的中点为M,GH的中点为N,下列结论正确的是( )
A.平面ABE B.平面ADE
C.平面BDH D.平面CDE
12.经过点作直线l,若直线l与连接,的线段总有公共点,则直线l的斜率k的取值范围为( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
13.若一直线的倾斜角为60°,则该直线的斜率为__________.
14.以点(1,2)为圆心,与直线相切的圆的方程是__________.
15.如图(1),长方体的棱和的中点分别为E,F,,,,则异面直线EF与所成角的正切值为__________.
16.据《九章算术》记载,“鳖臑(biēnào)”为四个面都是直角三角形的三棱锥.如图(2)所示,现有一个“鳖臑”,底面,,且,三棱锥外接球表面积为__________.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)设直线与相交于一点A.
(1)求点A的坐标;
(2)求经过点A,且垂直于直线的直线的方程.
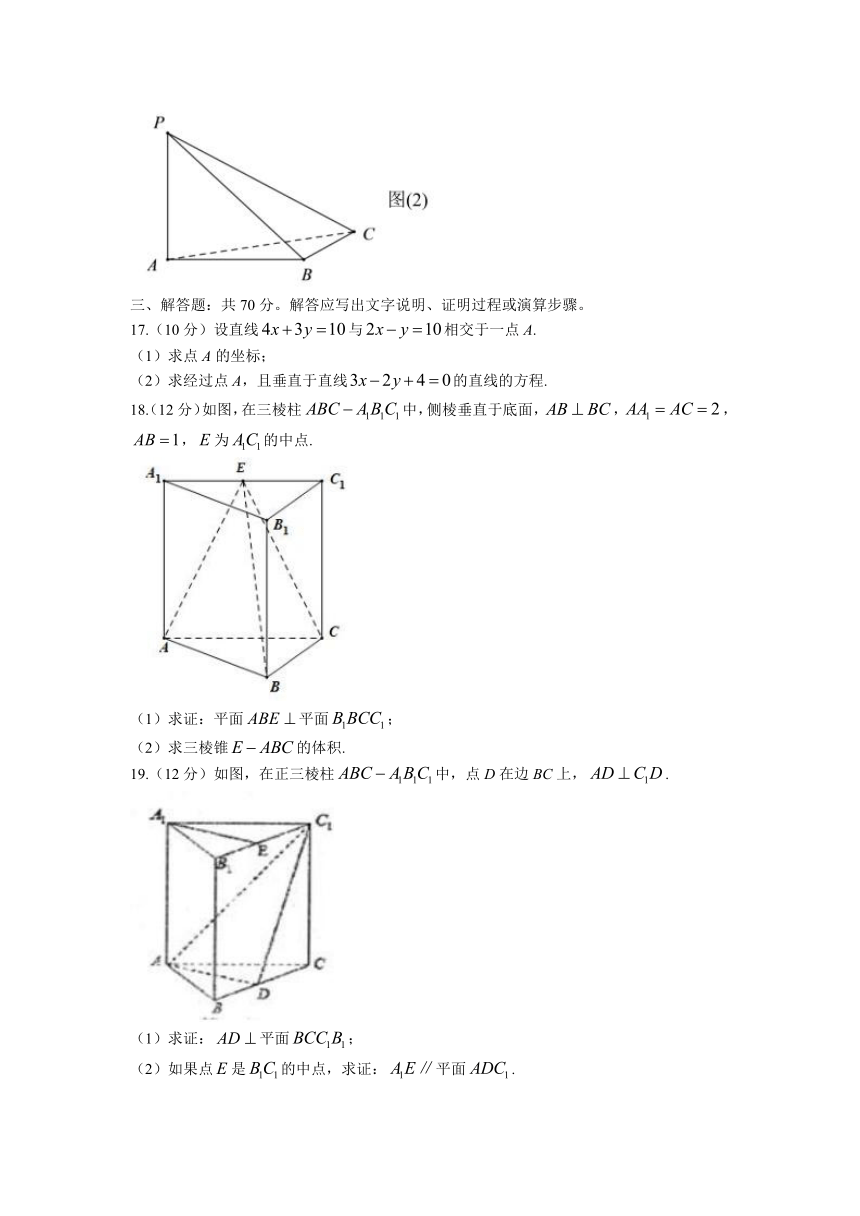
18.(12分)如图,在三棱柱中,侧棱垂直于底面,,,,为的中点.
(1)求证:平面平面;
(2)求三棱锥的体积.
19.(12分)如图,在正三棱柱中,点D在边BC上,.
(1)求证:平面;
(2)如果点是的中点,求证:平面.
20.(12分)一条光线从点射出,与轴相交于点,经轴反射,求入射光线和反射光线所在的直线方程
21.(12分)如图,圆柱的轴截面ABCD是正方形,点E是底面圆周上异于A,B的一点,,是垂足.
(1)证明:;
(2)若,当三棱锥体积最大时,求点C到平面BDE的距离.
22.(12分)已知点,点,直线过定点.
(1)求以线段AB为直径的圆的标准方程;
(2)记(1)中求得的圆的圆心为C,
(i)若直线l与圆C相切,求直线l的方程;
(ⅱ)若直线l与圆C交于,PQ两点,求面积的最大值,并求此时直线l的方程.
高二数学答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
C A D C B B D B A A C A
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(1)由,解得,因此,点的坐标为;
(2)因为直线的斜率为,
所以垂直于直线的直线斜率为,
则过点,且垂直于直线的直线的方程为,
即:.
18.解:(1)在三棱柱中,
因为底面,所以,
又因为,所以平面,
因为平面,所以平面平面.
(2)因为,,,
所以,
所以三棱锥的体积为:.
19.证:(1)∵面,面,∴,
又∵,,∴平面.
(2)因为平面,所以.
从而是中点.连接,则.
∴四边形是平行四边形,∴.∵面,面,
∴平面.
20.解:依题可知入射光线所在直线为直线,而,
由直线的方程为,即为入射光线所在直线方程.
又由可知直线的倾斜角为45°,又入射光线和反射光线
关于直线对称,所以易知反射光线所在直线倾斜角为135°,
所以反射光线所在直线斜率为-1,又过点,
所以反射光线所在直线方程为即.
21.解:(1)由圆柱性质可知,平面,
∵平面,∴.
∵是圆柱底面的直径,点在圆周上,
∴,又,∴平面,
∵平面,∴,
又∵,且,
∴平面,∵平面,∴
(2),,
当最大时,即最大,即是等腰直角三角形时,
∵,∴,,
并且点到平面的距离就是点E到直线AB的距离,
设点C到平面EBD的距离为h,则
,
解得:.
22.解:(1)依题可知线段AB的中点为是圆心
半径.
所以所求圆的标准方程为:.
(2)(i)由(1)知:圆心,半径,
当直线斜率不存在时,方程为,是圆的切线,满足题意;
当直线斜率存在时,设其方程为,即,
∴圆心到直线距离,解得:,∴:;
综上所述:直线的方程为或;
(ⅱ)由直线与圆交于,两点知:直线斜率存在且不为0,
设其方程为:,即,
∴圆心到直线距离,
∵
(当且仅当,即时取等号),
由得:,解得:或,
∴面积的最大值为2,此时方程为:或.
一、单项选择题:本题共12小题,每小题5分,共60分。
1.已知,,则( )
A.3 B.4 C.5 D.6
2.过两点,的直线方程为( )
A. B.
C. D.
3.直线在轴上的截距为( )
A. B. C.2 D.-2
4.如果空间四点A,B,C,D不共面,那么下列判断中正确的是( )
A.A,B,C,D四点中必有三点共线 B.直线AB与CD相交
C.A,B,C,D四点中不存在三点共线 D.直线AB与CD平行
5.已知直线:,:,则,之间的距离为( )
A.1 B. C. D.2
6.已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.与圆:同圆心,且面积为面积的一半的圆的方程为( )
A. B.
C. D.
8.在下列关于直线l,m和平面,的命题中真命题是( )
A.若且,则 B.若且,则
C.若且,则 D.若且,则
9.某几何体的三视图如图所示,则该几何体的表面积为( )
A. B. C. D.
10.已知直线:与直线:平行,则实数为( )
A.3 B.-2 C.3或-2 D.以上都不对
11.一个正方体的平面展开图及该正方体的直观图如图所示,在正方体中,设BC的中点为M,GH的中点为N,下列结论正确的是( )
A.平面ABE B.平面ADE
C.平面BDH D.平面CDE
12.经过点作直线l,若直线l与连接,的线段总有公共点,则直线l的斜率k的取值范围为( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
13.若一直线的倾斜角为60°,则该直线的斜率为__________.
14.以点(1,2)为圆心,与直线相切的圆的方程是__________.
15.如图(1),长方体的棱和的中点分别为E,F,,,,则异面直线EF与所成角的正切值为__________.
16.据《九章算术》记载,“鳖臑(biēnào)”为四个面都是直角三角形的三棱锥.如图(2)所示,现有一个“鳖臑”,底面,,且,三棱锥外接球表面积为__________.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)设直线与相交于一点A.
(1)求点A的坐标;
(2)求经过点A,且垂直于直线的直线的方程.
18.(12分)如图,在三棱柱中,侧棱垂直于底面,,,,为的中点.
(1)求证:平面平面;
(2)求三棱锥的体积.
19.(12分)如图,在正三棱柱中,点D在边BC上,.
(1)求证:平面;
(2)如果点是的中点,求证:平面.
20.(12分)一条光线从点射出,与轴相交于点,经轴反射,求入射光线和反射光线所在的直线方程
21.(12分)如图,圆柱的轴截面ABCD是正方形,点E是底面圆周上异于A,B的一点,,是垂足.
(1)证明:;
(2)若,当三棱锥体积最大时,求点C到平面BDE的距离.
22.(12分)已知点,点,直线过定点.
(1)求以线段AB为直径的圆的标准方程;
(2)记(1)中求得的圆的圆心为C,
(i)若直线l与圆C相切,求直线l的方程;
(ⅱ)若直线l与圆C交于,PQ两点,求面积的最大值,并求此时直线l的方程.
高二数学答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
C A D C B B D B A A C A
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(1)由,解得,因此,点的坐标为;
(2)因为直线的斜率为,
所以垂直于直线的直线斜率为,
则过点,且垂直于直线的直线的方程为,
即:.
18.解:(1)在三棱柱中,
因为底面,所以,
又因为,所以平面,
因为平面,所以平面平面.
(2)因为,,,
所以,
所以三棱锥的体积为:.
19.证:(1)∵面,面,∴,
又∵,,∴平面.
(2)因为平面,所以.
从而是中点.连接,则.
∴四边形是平行四边形,∴.∵面,面,
∴平面.
20.解:依题可知入射光线所在直线为直线,而,
由直线的方程为,即为入射光线所在直线方程.
又由可知直线的倾斜角为45°,又入射光线和反射光线
关于直线对称,所以易知反射光线所在直线倾斜角为135°,
所以反射光线所在直线斜率为-1,又过点,
所以反射光线所在直线方程为即.
21.解:(1)由圆柱性质可知,平面,
∵平面,∴.
∵是圆柱底面的直径,点在圆周上,
∴,又,∴平面,
∵平面,∴,
又∵,且,
∴平面,∵平面,∴
(2),,
当最大时,即最大,即是等腰直角三角形时,
∵,∴,,
并且点到平面的距离就是点E到直线AB的距离,
设点C到平面EBD的距离为h,则
,
解得:.
22.解:(1)依题可知线段AB的中点为是圆心
半径.
所以所求圆的标准方程为:.
(2)(i)由(1)知:圆心,半径,
当直线斜率不存在时,方程为,是圆的切线,满足题意;
当直线斜率存在时,设其方程为,即,
∴圆心到直线距离,解得:,∴:;
综上所述:直线的方程为或;
(ⅱ)由直线与圆交于,两点知:直线斜率存在且不为0,
设其方程为:,即,
∴圆心到直线距离,
∵
(当且仅当,即时取等号),
由得:,解得:或,
∴面积的最大值为2,此时方程为:或.
同课章节目录
