人教版五年级下册4 分数的意义和性质练习十三(课件18张PPT)
文档属性
| 名称 | 人教版五年级下册4 分数的意义和性质练习十三(课件18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
人教版数学五年级(下)
练习十三
分数的意义和性质
4
重点回顾
做一做,说一说。
(1)
圈出下面分数中的真分数,说一说剩下的假分数哪些可以化成整数,哪些可以化成带分数?
6
5
18
7
5
11
8
53
12
36
2
1
15
31
17
34
4
4
可以化成整数的有:
可以化成带分数的有:
分子是分母的倍数
分子不是分母的倍数
分子比分母小的分数叫做真分数,分子比分母大或分子和分母相等的分数叫做假分数,假分数可以化成整数或带分数。
(2)将上面的假分数化成整数或带分数。
12
36
17
34
4
4
5
11
8
53
15
31
12
36
=36÷12=3
17
34
=34÷17=2
4
4
=4÷4=1
5
11
=11÷5=2
5
1
8
53
=53÷8=6
8
5
15
31
=31÷15=2
15
1
假分数化成整数或带分数的方法:用假分数的分子除以分母,如果没有余数,结果(商)是整数;如果有余数,结果 是带分数。
分母
余数
(商 )
( )
( )
练习巩固
(教材第55页练习十三)
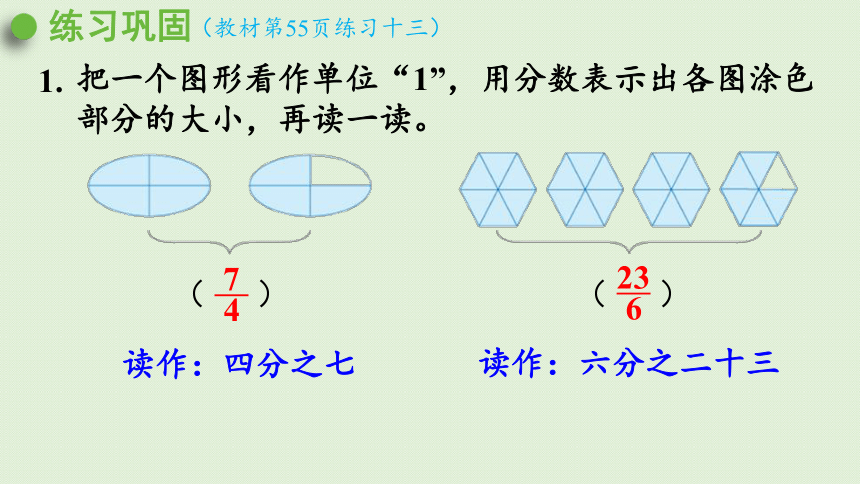
1.
把一个图形看作单位“1”,用分数表示出各图涂色部分的大小,再读一读。
4
7
读作:四分之七
6
23
读作:六分之二十三
2.
下面的说法对吗?为什么?
(1)我吃了一个西瓜的 。 ( )
(2)爷爷把一块菜地的 种了西红柿, 种了茄子, 种了辣椒。 ( )
(3)一块巧克力,我吃了 ,表哥吃了 。 ( )
4
5
5
3
5
2
5
1
6
5
6
1
×
因为一个西瓜平均分成4份,4份全部吃完是这个西瓜的 ,所以吃了 是不可能的。
4
4
4
5
×
因为一块菜地平均分成5份,3份种西红柿,2份种茄子,地就种满了,种不了辣椒。
√
因为一块巧克力平均分成6份,我吃了5份,表哥吃了1份,刚好吃完。
3÷3 =
3
3
3. (1)3个人平均分,每人分 杯,也就是 杯。
( )
( )
(2)2个人平均分,每人分 杯。
3
3
1(杯)
=
3÷2 =
2
3
(杯)
1
2
3
3
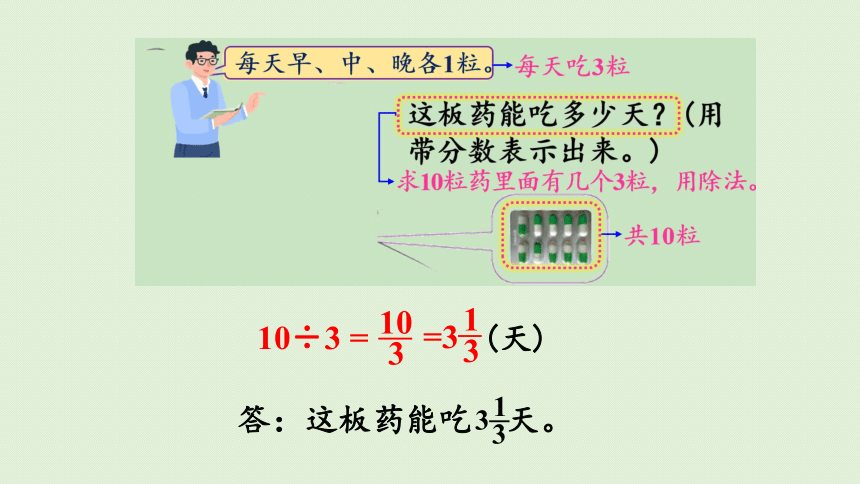
10
10÷3 =
3
1
=3
答:这板药能吃 天。
3
1
3
(天)
5.
在直线上面的 里填上适当的假分数,下面的 里填上适当的带分数。
0
1
2
3
4
5
5
5
10
5
20
5
8
5
12
5
15
5
18
5
1
1
5
4
2
5
3
3
5
6
5
7
5
11
5
13
5
14
5
16
5
17
5
1
5
2
5
3
5
1
5
2
6.
把一个物体看作单位“1”,用分数表示下面各图涂色部分的大小。
2
1
3
( )
( )
3
1
2
7.
5
7
7÷5 =
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
熊冬眠约 5 个月
睡鼠冬眠约 7 个月
7
5
5÷7 =
答:睡鼠的冬眠时间是熊的 ,熊的冬眠时间是睡鼠的 。
7
5
5
7
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
真分数是分子比分母小的分数。
(2)写出分子是7的所有假分数。
(1)
分母是7的真分数,其分子一定小于7。
分子可能是1,2,3,4,5,6。
(1)分母是7的真分数有:
7
1
7
2
7
3
7
4
7
5
7
6
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
(2)写出分子是7的所有假分数。
假分数是分子比分母大或分子和分母相等的分数。
(2)
分子是7的假分数,其分母一定等于或小于7。
分子可能是1,2,3,4,5,6,7。
规范解答
(2)分子是7的假分数有:
1
7
2
7
3
7
4
7
5
7
6
7
7
7
9.
在 里填上“>”“<”或“=”。
9
7
9
7
1
75
25
25
1
3
46
12
4
9
2
8
74
9
<
>
<
=
真分数<1
带分数>1
76
25
3
10
12
3
48
12
74
9
2
9
8
你认为带分数和假分数哪个更容易看出数的大小?
一般情况下,将假分数化成带分数或整数再比较容易些。
当然是带分数啦。
10. 指出下表中哪些是真分数,哪些是假分数。把等于 1 的假分数涂上颜色。
真分数
假分数
你发现了什么?
=1
<1
>1
发现:真分数的分子比分母小,假分数的分子大于或等于分母。1 可以写成任何非0自然数为分母的分数。
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5……你能把30写成几个质数相乘的形式吗?
拓展提升
解决问题
逐步分解法。
方法一
(1)把30写成两个整数相乘的形式。如:30=2×15。
30
2
15
(2)判断两个因数是不是都是质数。2是质数,不需要再分解;15是合数,需要再分解,15分解成3×5。
3
5
(3)2,3,5都是质数,不需要再分解。
= 2×3×5
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5,……你能把30写成几个质数相乘的形式吗?
拓展提升
解决问题
短除法。
方法二
3 0
2
1 5
(2)用 30 的因数中的质数去除,一般从最小的质数开始,写在短除号左侧,每次除得的商写在短除号的下面。一直除到商是质数为止。
3
5
(3)把30写出除数和最后的商相乘的形式。
30 = 2×3×5
(1)把要分解的30写在短除号 里。
认识质因数和分解质因数
2
15
3
5
30
= 2×3×5
30 = 2×3×5
3 0
2
1 5
3
5
质数
质数
质数
像 30 = 2×3×5 这样,每个合数都可以写成几个质数相乘的形式,我们就把其中的每个质数叫做这个合数的质因数。把一个合数用质因数相乘的形式表示出来,就叫做分解质因数。
试一试
(1)把12分解质因数,正确的是( )。
12=3×4 B. 12=2×2×3
C. 12=2×6 D. 12=2×2×3×1
合数
合数
不是
质数
B
(2)把下面各数分解质因数。
8
24
75
8
2
4
2
2
8 = 2×2×2
2 4
2
1 2
2
6
24 = 2×2×2×3
2
3
7 5
3
2 5
5
5
75 = 3×5×5
人教版数学五年级(下)
练习十三
分数的意义和性质
4
重点回顾
做一做,说一说。
(1)
圈出下面分数中的真分数,说一说剩下的假分数哪些可以化成整数,哪些可以化成带分数?
6
5
18
7
5
11
8
53
12
36
2
1
15
31
17
34
4
4
可以化成整数的有:
可以化成带分数的有:
分子是分母的倍数
分子不是分母的倍数
分子比分母小的分数叫做真分数,分子比分母大或分子和分母相等的分数叫做假分数,假分数可以化成整数或带分数。
(2)将上面的假分数化成整数或带分数。
12
36
17
34
4
4
5
11
8
53
15
31
12
36
=36÷12=3
17
34
=34÷17=2
4
4
=4÷4=1
5
11
=11÷5=2
5
1
8
53
=53÷8=6
8
5
15
31
=31÷15=2
15
1
假分数化成整数或带分数的方法:用假分数的分子除以分母,如果没有余数,结果(商)是整数;如果有余数,结果 是带分数。
分母
余数
(商 )
( )
( )
练习巩固
(教材第55页练习十三)
1.
把一个图形看作单位“1”,用分数表示出各图涂色部分的大小,再读一读。
4
7
读作:四分之七
6
23
读作:六分之二十三
2.
下面的说法对吗?为什么?
(1)我吃了一个西瓜的 。 ( )
(2)爷爷把一块菜地的 种了西红柿, 种了茄子, 种了辣椒。 ( )
(3)一块巧克力,我吃了 ,表哥吃了 。 ( )
4
5
5
3
5
2
5
1
6
5
6
1
×
因为一个西瓜平均分成4份,4份全部吃完是这个西瓜的 ,所以吃了 是不可能的。
4
4
4
5
×
因为一块菜地平均分成5份,3份种西红柿,2份种茄子,地就种满了,种不了辣椒。
√
因为一块巧克力平均分成6份,我吃了5份,表哥吃了1份,刚好吃完。
3÷3 =
3
3
3. (1)3个人平均分,每人分 杯,也就是 杯。
( )
( )
(2)2个人平均分,每人分 杯。
3
3
1(杯)
=
3÷2 =
2
3
(杯)
1
2
3
3
10
10÷3 =
3
1
=3
答:这板药能吃 天。
3
1
3
(天)
5.
在直线上面的 里填上适当的假分数,下面的 里填上适当的带分数。
0
1
2
3
4
5
5
5
10
5
20
5
8
5
12
5
15
5
18
5
1
1
5
4
2
5
3
3
5
6
5
7
5
11
5
13
5
14
5
16
5
17
5
1
5
2
5
3
5
1
5
2
6.
把一个物体看作单位“1”,用分数表示下面各图涂色部分的大小。
2
1
3
( )
( )
3
1
2
7.
5
7
7÷5 =
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
熊冬眠约 5 个月
睡鼠冬眠约 7 个月
7
5
5÷7 =
答:睡鼠的冬眠时间是熊的 ,熊的冬眠时间是睡鼠的 。
7
5
5
7
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
真分数是分子比分母小的分数。
(2)写出分子是7的所有假分数。
(1)
分母是7的真分数,其分子一定小于7。
分子可能是1,2,3,4,5,6。
(1)分母是7的真分数有:
7
1
7
2
7
3
7
4
7
5
7
6
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
(2)写出分子是7的所有假分数。
假分数是分子比分母大或分子和分母相等的分数。
(2)
分子是7的假分数,其分母一定等于或小于7。
分子可能是1,2,3,4,5,6,7。
规范解答
(2)分子是7的假分数有:
1
7
2
7
3
7
4
7
5
7
6
7
7
7
9.
在 里填上“>”“<”或“=”。
9
7
9
7
1
75
25
25
1
3
46
12
4
9
2
8
74
9
<
>
<
=
真分数<1
带分数>1
76
25
3
10
12
3
48
12
74
9
2
9
8
你认为带分数和假分数哪个更容易看出数的大小?
一般情况下,将假分数化成带分数或整数再比较容易些。
当然是带分数啦。
10. 指出下表中哪些是真分数,哪些是假分数。把等于 1 的假分数涂上颜色。
真分数
假分数
你发现了什么?
=1
<1
>1
发现:真分数的分子比分母小,假分数的分子大于或等于分母。1 可以写成任何非0自然数为分母的分数。
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5……你能把30写成几个质数相乘的形式吗?
拓展提升
解决问题
逐步分解法。
方法一
(1)把30写成两个整数相乘的形式。如:30=2×15。
30
2
15
(2)判断两个因数是不是都是质数。2是质数,不需要再分解;15是合数,需要再分解,15分解成3×5。
3
5
(3)2,3,5都是质数,不需要再分解。
= 2×3×5
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5,……你能把30写成几个质数相乘的形式吗?
拓展提升
解决问题
短除法。
方法二
3 0
2
1 5
(2)用 30 的因数中的质数去除,一般从最小的质数开始,写在短除号左侧,每次除得的商写在短除号的下面。一直除到商是质数为止。
3
5
(3)把30写出除数和最后的商相乘的形式。
30 = 2×3×5
(1)把要分解的30写在短除号 里。
认识质因数和分解质因数
2
15
3
5
30
= 2×3×5
30 = 2×3×5
3 0
2
1 5
3
5
质数
质数
质数
像 30 = 2×3×5 这样,每个合数都可以写成几个质数相乘的形式,我们就把其中的每个质数叫做这个合数的质因数。把一个合数用质因数相乘的形式表示出来,就叫做分解质因数。
试一试
(1)把12分解质因数,正确的是( )。
12=3×4 B. 12=2×2×3
C. 12=2×6 D. 12=2×2×3×1
合数
合数
不是
质数
B
(2)把下面各数分解质因数。
8
24
75
8
2
4
2
2
8 = 2×2×2
2 4
2
1 2
2
6
24 = 2×2×2×3
2
3
7 5
3
2 5
5
5
75 = 3×5×5
