北师大版九年级数学下册1.3 三角函数的计算课件(共25张PPT)
文档属性
| 名称 | 北师大版九年级数学下册1.3 三角函数的计算课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 22:06:38 | ||
图片预览







文档简介
(共25张PPT)
第一章 直角三角形的边角关系
1.3 三角函数的计算
随堂演练
课堂小结
获取新知
情景导入
例题讲解
情景导入
如图,当登山缆车的吊箱经过A点到达点B时,它走过了200 m,已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
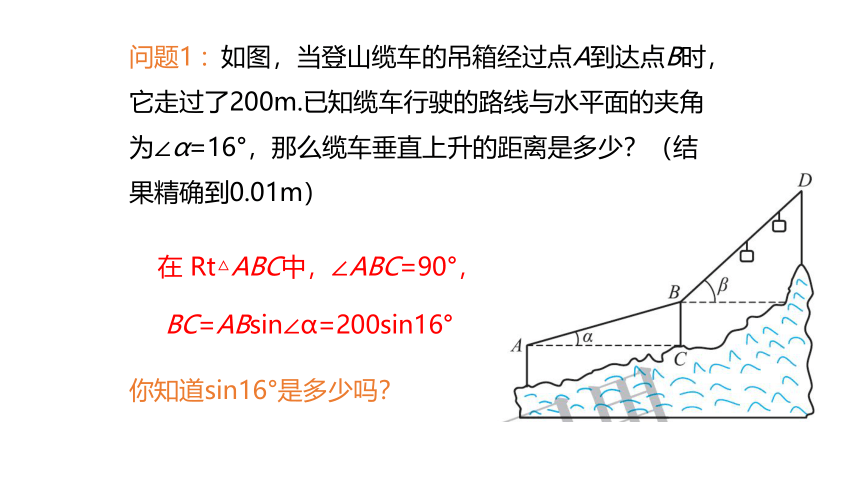
问题1 : 如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
在 Rt△ABC中,∠ABC=90°,
BC=ABsin∠α=200sin16°
你知道sin16°是多少吗?
获取新知
在Rt△ABC中,∠ACB=90°,BC=ABsin 16°=200sin 16°.
你知道sin 16°是多少吗?
我们可以借助科学计算器求锐角的三角函数值.怎样用科学计算器求三角函数值呢?
用计算器求三角函数值
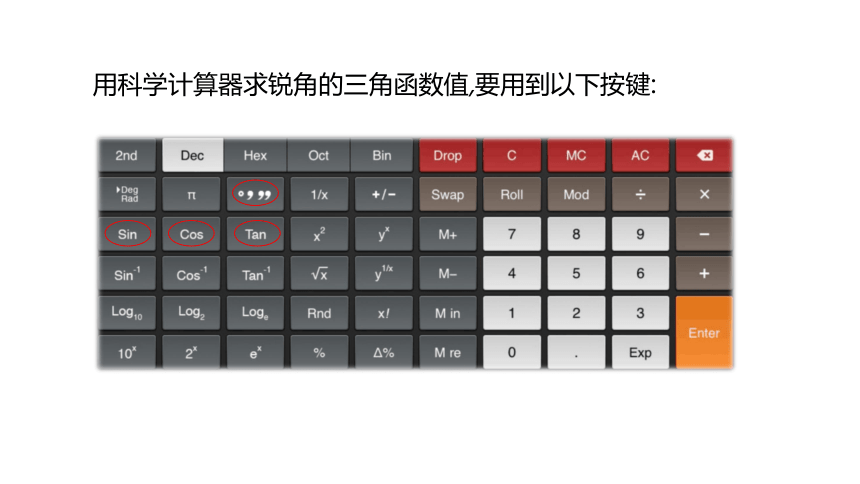
用科学计算器求锐角的三角函数值,要用到以下按键:
1.求sin16°.
第一步:按计算器 键,
sin
第二步:输入角度值16,
屏幕显示结果sin16°=0.2756373558
(也有的计算器是先输入角度再按函数名称键).
2.求cos72°.
第一步:按计算器 键,
cos
第二步:输入角度值72,
屏幕显示结果cos72°=0.309 016 994
第一步:按计算器 键,
tan
3.求 tan30°36'.
第二步:输入角度值30,按 键,输入36,按
°' ″
最后按等号,屏幕显示答案:0.591 398 351;
第一步:按计算器 键,
tan
第二步:输入角度值30.6 (因为30°36'=30.6°)
屏幕显示答案:0.591 398 351.
第一种方法:
第二种方法:
°' ″
键,
例1:用计算器求下列各式的值(精确到0.0001):
(1)sin47°; (2)sin12°30′;
(3)cos25°18′; (4)sin18°+cos55°-tan59°.
解:根据题意用计算器求出:
(1)sin47°≈0.7314;
(2)sin12°30′≈0.2164;
(3)cos25°18′≈0.9041;
(4)sin18°+cos55°-tan59°≈-0.7817.
例题讲解
为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建了40m长的斜道(如图).这条斜道的倾斜角是多少?
利用计算器由三角函数值求角度
获取新知
问题2 :如图,在Rt△ABC中, 那么∠A是多少度呢
要解决这个问题,我们可以借助科学计算器.
如何用计算器由锐角三角函数值求相应锐角的大小?
已知三角函数值求角度,要用到 sin 、cos 、tan 键的第二功能“sin-1,cos-1,tan-1”和 SHIFT 键.
例如:已知sin A=0.981 6,求锐角A;
已知cos A=0.860 7,求锐角A;
已知tan A=0.189 0,求锐角A;
已知tan A=56.78,求锐角A.
按键顺序 显示结果
sin A=0.981 6
cos A=0.860 7
tan A=0.189 0
tan A=56.78
SHIFT
sin
0
·
9
8
1
6
=
sin-10.981 6=
78.991 840 39
SHIFT
cos
0
·
8
6
0
7
=
cos-10.860 7=
30.604 730 07
SHIFT
tan
0
·
1
8
9
0
=
tan-10.189 0=
10.702 657 49
SHIFT
tan
5
·
6
7
8
=
tan-156.78=
88.991 020 49
上表的显示结果是以“度”为单位的,再按 ′ ″ 键即可显示以“度、分、秒”为单位的结果.
根据上述方法你能求出问题2中∠A的大小吗?
按键顺序和显示结果为
SHIFT
sin
0
·
2
5
=
14.477 512 19°
再按 ° ′ ″ 键可显示14 28′39″,所以∠A=14 28′39″.
所以问题1中∠A的读数是14 28′39″.
例2 根据下列条件求锐角A的度数:(结果精确到1′)
(1)sin A=0.732 1;(2)cos A=0.218 7;(3)tan A=3.527.
解:(1)先按SHIFT sin 0.7321=键,显示:47.062 734 57,
再按°’”键,即可显示47°3′45.84″,所以∠A≈47°4′.
(2)先按 SHIFT cos 0.2187=键,显示:77.367 310 78,
再按°’”键,显示77°22′2.32″,所以∠A≈77°22′.
(3)先按 SHIFT tan 3.527=键,显示:74.170 530 81,
再按°’”键,显示74°10′13.91″,所以∠A≈74°10′.
例题讲解
cos55°=
cos70°=
cos74°28 '=
tan3°8 ' =
tan80°25'43″=
sin20°=
sin35°=
sin15°32 ' =
0.3420
0.3420
0.5736
0.5736
0.2678
0.2678
5.930
0.0547
角度增大
正弦值增大
余弦值减小
正切值增大
比一比,你能得出什么结论?
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
归纳总结
随堂演练
1.用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin45°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
D
2. 已知sin α= ,求α,若用科学计算器计算且结果以“度、分、秒”为单位,最后按键( )
A.AC/ON B. SHIFT
C.MODE D. °′ ″
D
3.用计算器求下列各式的值(精确到0.0001):
(1)sin47°; (2)sin12°30′;
(3)cos25°18′; (4)sin18°+cos55°-tan59°.
解:根据题意用计算器求出:
(1)sin47°≈0.7314;
(2)sin12°30′≈0.2164;
(3)cos25°18′≈0.9041;
(4)sin18°+cos55°-tan59°≈-0.7817.
4. 根据下列条件求锐角θ的大小:
(1)tan θ=2.988 8;
(2)sin θ=0.395 7;
(3)cos θ=0.785 0;
(4)tan θ=0.897 2.
θ=71 30′2″
θ=23 18′35″
θ=38 16′46″
θ=41 53′54″
5.如图所示,电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
解析 (1)利用△ABC是等腰直角三角形易得AC的长;
(2)在Rt△BDE中,运用直角三角形的边角关系即可求出BE的长,用AB的长减去BE的长度即可.
课堂小结
第一章 直角三角形的边角关系
1.3 三角函数的计算
随堂演练
课堂小结
获取新知
情景导入
例题讲解
情景导入
如图,当登山缆车的吊箱经过A点到达点B时,它走过了200 m,已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
问题1 : 如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
在 Rt△ABC中,∠ABC=90°,
BC=ABsin∠α=200sin16°
你知道sin16°是多少吗?
获取新知
在Rt△ABC中,∠ACB=90°,BC=ABsin 16°=200sin 16°.
你知道sin 16°是多少吗?
我们可以借助科学计算器求锐角的三角函数值.怎样用科学计算器求三角函数值呢?
用计算器求三角函数值
用科学计算器求锐角的三角函数值,要用到以下按键:
1.求sin16°.
第一步:按计算器 键,
sin
第二步:输入角度值16,
屏幕显示结果sin16°=0.2756373558
(也有的计算器是先输入角度再按函数名称键).
2.求cos72°.
第一步:按计算器 键,
cos
第二步:输入角度值72,
屏幕显示结果cos72°=0.309 016 994
第一步:按计算器 键,
tan
3.求 tan30°36'.
第二步:输入角度值30,按 键,输入36,按
°' ″
最后按等号,屏幕显示答案:0.591 398 351;
第一步:按计算器 键,
tan
第二步:输入角度值30.6 (因为30°36'=30.6°)
屏幕显示答案:0.591 398 351.
第一种方法:
第二种方法:
°' ″
键,
例1:用计算器求下列各式的值(精确到0.0001):
(1)sin47°; (2)sin12°30′;
(3)cos25°18′; (4)sin18°+cos55°-tan59°.
解:根据题意用计算器求出:
(1)sin47°≈0.7314;
(2)sin12°30′≈0.2164;
(3)cos25°18′≈0.9041;
(4)sin18°+cos55°-tan59°≈-0.7817.
例题讲解
为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建了40m长的斜道(如图).这条斜道的倾斜角是多少?
利用计算器由三角函数值求角度
获取新知
问题2 :如图,在Rt△ABC中, 那么∠A是多少度呢
要解决这个问题,我们可以借助科学计算器.
如何用计算器由锐角三角函数值求相应锐角的大小?
已知三角函数值求角度,要用到 sin 、cos 、tan 键的第二功能“sin-1,cos-1,tan-1”和 SHIFT 键.
例如:已知sin A=0.981 6,求锐角A;
已知cos A=0.860 7,求锐角A;
已知tan A=0.189 0,求锐角A;
已知tan A=56.78,求锐角A.
按键顺序 显示结果
sin A=0.981 6
cos A=0.860 7
tan A=0.189 0
tan A=56.78
SHIFT
sin
0
·
9
8
1
6
=
sin-10.981 6=
78.991 840 39
SHIFT
cos
0
·
8
6
0
7
=
cos-10.860 7=
30.604 730 07
SHIFT
tan
0
·
1
8
9
0
=
tan-10.189 0=
10.702 657 49
SHIFT
tan
5
·
6
7
8
=
tan-156.78=
88.991 020 49
上表的显示结果是以“度”为单位的,再按 ′ ″ 键即可显示以“度、分、秒”为单位的结果.
根据上述方法你能求出问题2中∠A的大小吗?
按键顺序和显示结果为
SHIFT
sin
0
·
2
5
=
14.477 512 19°
再按 ° ′ ″ 键可显示14 28′39″,所以∠A=14 28′39″.
所以问题1中∠A的读数是14 28′39″.
例2 根据下列条件求锐角A的度数:(结果精确到1′)
(1)sin A=0.732 1;(2)cos A=0.218 7;(3)tan A=3.527.
解:(1)先按SHIFT sin 0.7321=键,显示:47.062 734 57,
再按°’”键,即可显示47°3′45.84″,所以∠A≈47°4′.
(2)先按 SHIFT cos 0.2187=键,显示:77.367 310 78,
再按°’”键,显示77°22′2.32″,所以∠A≈77°22′.
(3)先按 SHIFT tan 3.527=键,显示:74.170 530 81,
再按°’”键,显示74°10′13.91″,所以∠A≈74°10′.
例题讲解
cos55°=
cos70°=
cos74°28 '=
tan3°8 ' =
tan80°25'43″=
sin20°=
sin35°=
sin15°32 ' =
0.3420
0.3420
0.5736
0.5736
0.2678
0.2678
5.930
0.0547
角度增大
正弦值增大
余弦值减小
正切值增大
比一比,你能得出什么结论?
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
归纳总结
随堂演练
1.用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin45°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
D
2. 已知sin α= ,求α,若用科学计算器计算且结果以“度、分、秒”为单位,最后按键( )
A.AC/ON B. SHIFT
C.MODE D. °′ ″
D
3.用计算器求下列各式的值(精确到0.0001):
(1)sin47°; (2)sin12°30′;
(3)cos25°18′; (4)sin18°+cos55°-tan59°.
解:根据题意用计算器求出:
(1)sin47°≈0.7314;
(2)sin12°30′≈0.2164;
(3)cos25°18′≈0.9041;
(4)sin18°+cos55°-tan59°≈-0.7817.
4. 根据下列条件求锐角θ的大小:
(1)tan θ=2.988 8;
(2)sin θ=0.395 7;
(3)cos θ=0.785 0;
(4)tan θ=0.897 2.
θ=71 30′2″
θ=23 18′35″
θ=38 16′46″
θ=41 53′54″
5.如图所示,电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
解析 (1)利用△ABC是等腰直角三角形易得AC的长;
(2)在Rt△BDE中,运用直角三角形的边角关系即可求出BE的长,用AB的长减去BE的长度即可.
课堂小结
