北师大版九年级数学下册:3.5 确定圆的条件课件(共27张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:3.5 确定圆的条件课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 23:44:49 | ||
图片预览





文档简介
(共27张PPT)
第三章 圆
3.5 确定圆的条件
例题讲解
随堂演练
情景导入
获取新知
知识回顾
课堂总结
知识回顾
问题 构成圆的基本要素有哪些
两个条件:
圆心
半径
o
r
情景引入
如图,你能将旋转木马破碎的圆形底座还原,以帮助考古学家画进行深入的研究吗?
想一想:要确定一个圆必须满足什么条件
获取新知
探索一
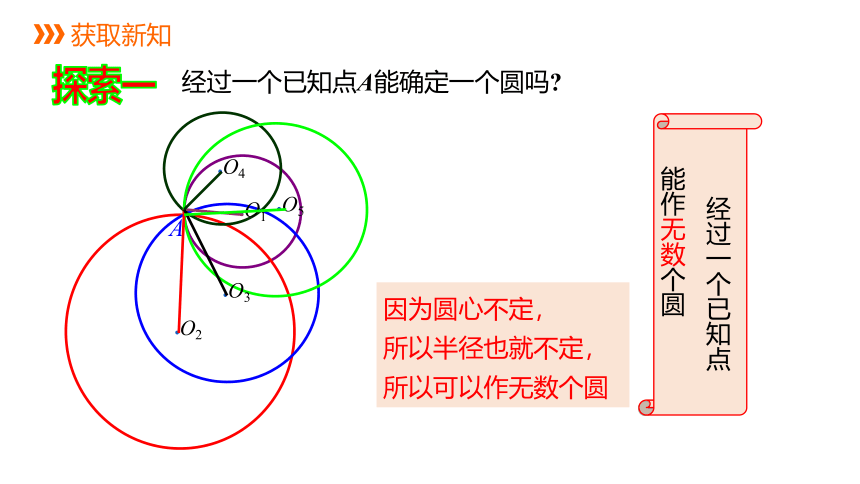
经过一个已知点A能确定一个圆吗
A
●O1
●O2
●O3
●O5
●O4
经过一个已知点
能作无数个圆
因为圆心不定,
所以半径也就不定,
所以可以作无数个圆
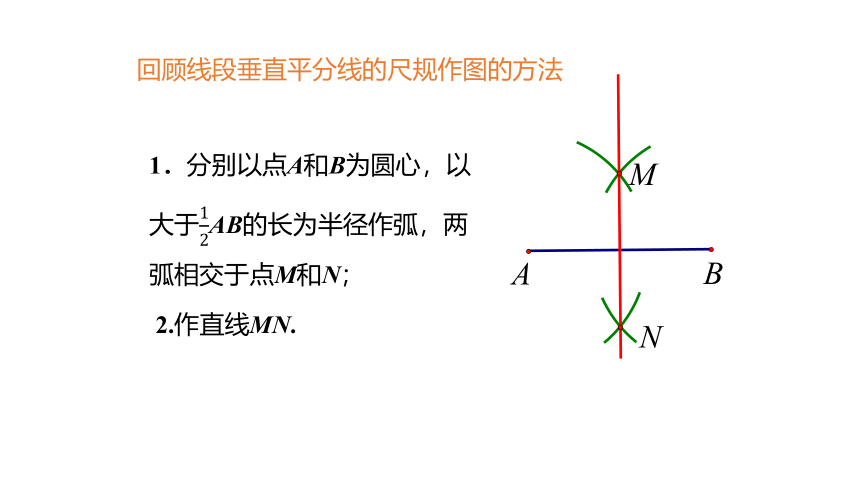
回顾线段垂直平分线的尺规作图的方法
1.分别以点A和B为圆心,以
大于AB的长为半径作弧,两弧相交于点M和N;
2.作直线MN.
N
M
A
B
探索二
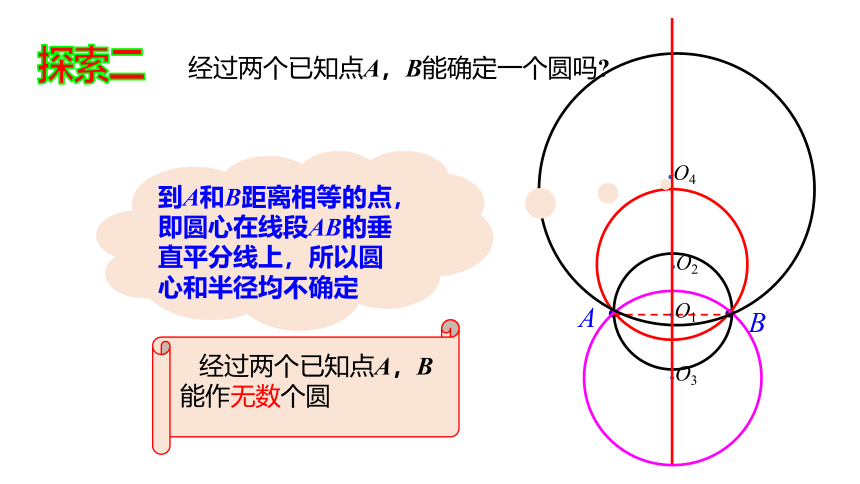
经过两个已知点A,B能确定一个圆吗
A
B
●O1
●O2
●O3
●O4
到A和B距离相等的点,即圆心在线段AB的垂直平分线上,所以圆心和半径均不确定
经过两个已知点A,B能作无数个圆
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
过不在同一直线上的三点A,B,C能不能确定一个圆
探索三
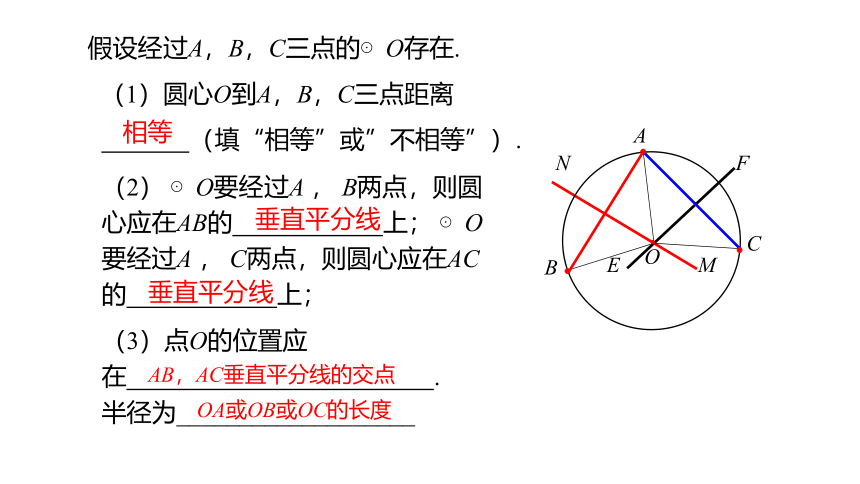
假设经过A,B,C三点的⊙O存在.
(1)圆心O到A,B,C三点距离
(填“相等”或”不相等”).
(2) ⊙O要经过A , B两点,则圆心应在AB的 上; ⊙O要经过A , C两点,则圆心应在AC的 上;
(3)点O的位置应在 .
半径为___________________
相等
垂直平分线
垂直平分线
AB,AC垂直平分线的交点
OA或OB或OC的长度
N
M
F
E
O
A
B
C
过如下三点能不能作圆 为什么
A
B
C
不能.因为圆心不存在
不在同一直线上的三点确定一个圆
位置关系
有且只有
例题讲解
例1 如图①是一个残破的圆轮,李师傅想要再浇铸一个同样大小的圆轮,你能想办法帮助李师傅吗?
解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所在的圆
获取新知
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
C
A
B
O
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
性质:三角形的外心到三角形三个顶点的距离相等.
作图:三角形三条边的垂直平分线的交点.
●O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
议一议
例2 如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
例题讲解
(2)∵点D的坐标是(0,3),
∴OD=3.在Rt△AOD中,
OA=OD·tan∠ADO= ,
AD=2OD=6,
∴点A的坐标是( ,0).
∵∠AOD=90°,
∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
如图所示,△ ABC 内接于⊙ O,∠ C=45 °,AB=4,求⊙ O 的半径.
例3
导引:
要求⊙O的半径,已知弦AB的长,需以AB为边与⊙O的半径(或直径)构成等腰直角三角形,因此有两个切入点.方法一:如图2,连接OA,OB,利用圆周角定理可得∠AOB=2∠C=90°,再利用勾股定理求出半径;方法二:如图2,作直径AD,连接BD,
利用同弧所对的圆周角相等,得
∠D=∠C=45°,再利用勾股
定理可求出半径.
图2
解:
方法一:如图1,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图1
方法二:如图2,作直径AD,连接BD,设⊙O的半径为r.
∵AD为⊙O的直径,
∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°.
∴BD=AB=4.
在Rt△ABD中,AB2+BD2=AD2,即42+42=(2r)2
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图2
求三角形的外接圆半径时,最常用的办法是作出圆心与三角形顶点的连线(即半径),延长使这条半径变为直径,将求半径转化为直角三角形中求边的长.
归纳总结
随堂演练
1.下列命题不正确的是( )
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
C
2.三角形的外心具有的性质是( )
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
B
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
4.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
C
5. 过两点A,B的圆有 个,这些圆的圆心都在线段AB的 _ 上;过 _ 的三点的圆有且只有一个.
无数
垂直平分线
不在同一直线上
6.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
7. 小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,如图,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
解:如图所示,☉O就是花坛的位置
课堂小结
第三章 圆
3.5 确定圆的条件
例题讲解
随堂演练
情景导入
获取新知
知识回顾
课堂总结
知识回顾
问题 构成圆的基本要素有哪些
两个条件:
圆心
半径
o
r
情景引入
如图,你能将旋转木马破碎的圆形底座还原,以帮助考古学家画进行深入的研究吗?
想一想:要确定一个圆必须满足什么条件
获取新知
探索一
经过一个已知点A能确定一个圆吗
A
●O1
●O2
●O3
●O5
●O4
经过一个已知点
能作无数个圆
因为圆心不定,
所以半径也就不定,
所以可以作无数个圆
回顾线段垂直平分线的尺规作图的方法
1.分别以点A和B为圆心,以
大于AB的长为半径作弧,两弧相交于点M和N;
2.作直线MN.
N
M
A
B
探索二
经过两个已知点A,B能确定一个圆吗
A
B
●O1
●O2
●O3
●O4
到A和B距离相等的点,即圆心在线段AB的垂直平分线上,所以圆心和半径均不确定
经过两个已知点A,B能作无数个圆
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
过不在同一直线上的三点A,B,C能不能确定一个圆
探索三
假设经过A,B,C三点的⊙O存在.
(1)圆心O到A,B,C三点距离
(填“相等”或”不相等”).
(2) ⊙O要经过A , B两点,则圆心应在AB的 上; ⊙O要经过A , C两点,则圆心应在AC的 上;
(3)点O的位置应在 .
半径为___________________
相等
垂直平分线
垂直平分线
AB,AC垂直平分线的交点
OA或OB或OC的长度
N
M
F
E
O
A
B
C
过如下三点能不能作圆 为什么
A
B
C
不能.因为圆心不存在
不在同一直线上的三点确定一个圆
位置关系
有且只有
例题讲解
例1 如图①是一个残破的圆轮,李师傅想要再浇铸一个同样大小的圆轮,你能想办法帮助李师傅吗?
解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所在的圆
获取新知
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
C
A
B
O
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
性质:三角形的外心到三角形三个顶点的距离相等.
作图:三角形三条边的垂直平分线的交点.
●O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
议一议
例2 如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
例题讲解
(2)∵点D的坐标是(0,3),
∴OD=3.在Rt△AOD中,
OA=OD·tan∠ADO= ,
AD=2OD=6,
∴点A的坐标是( ,0).
∵∠AOD=90°,
∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
如图所示,△ ABC 内接于⊙ O,∠ C=45 °,AB=4,求⊙ O 的半径.
例3
导引:
要求⊙O的半径,已知弦AB的长,需以AB为边与⊙O的半径(或直径)构成等腰直角三角形,因此有两个切入点.方法一:如图2,连接OA,OB,利用圆周角定理可得∠AOB=2∠C=90°,再利用勾股定理求出半径;方法二:如图2,作直径AD,连接BD,
利用同弧所对的圆周角相等,得
∠D=∠C=45°,再利用勾股
定理可求出半径.
图2
解:
方法一:如图1,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图1
方法二:如图2,作直径AD,连接BD,设⊙O的半径为r.
∵AD为⊙O的直径,
∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°.
∴BD=AB=4.
在Rt△ABD中,AB2+BD2=AD2,即42+42=(2r)2
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图2
求三角形的外接圆半径时,最常用的办法是作出圆心与三角形顶点的连线(即半径),延长使这条半径变为直径,将求半径转化为直角三角形中求边的长.
归纳总结
随堂演练
1.下列命题不正确的是( )
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
C
2.三角形的外心具有的性质是( )
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
B
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
4.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
C
5. 过两点A,B的圆有 个,这些圆的圆心都在线段AB的 _ 上;过 _ 的三点的圆有且只有一个.
无数
垂直平分线
不在同一直线上
6.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
7. 小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,如图,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
解:如图所示,☉O就是花坛的位置
课堂小结
