北师大版九年级数学下册:3.6 第2课时切线的判定课件(共23张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:3.6 第2课时切线的判定课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 23:49:21 | ||
图片预览



文档简介
(共23张PPT)
第三章 圆
3.6 第2课时 切线的判定
例题讲解
随堂演练
情景导入
获取新知
知识回顾
课堂总结
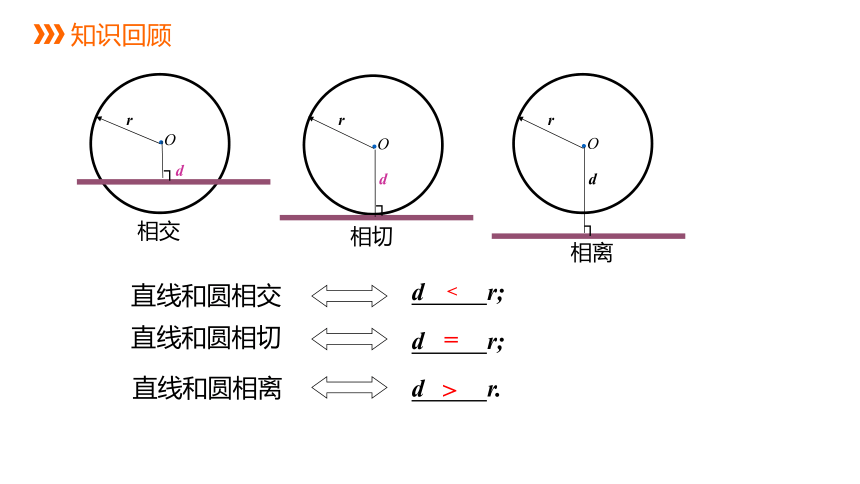
知识回顾
d r;
d r;
直线和圆相切
直线和圆相离
d r.
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
直线和圆相交
情景引入
砂轮上打磨工件时飞出的火星
下图中让你感受到了直线与圆的哪种位置关系?如何判断一条直线是否为圆的切线呢?
获取新知
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
圆心O到直线l的距离就是OA的长度,也就是r
直线l与⊙O是相切关系
l
O
A
┐
知识点一:切线的判定
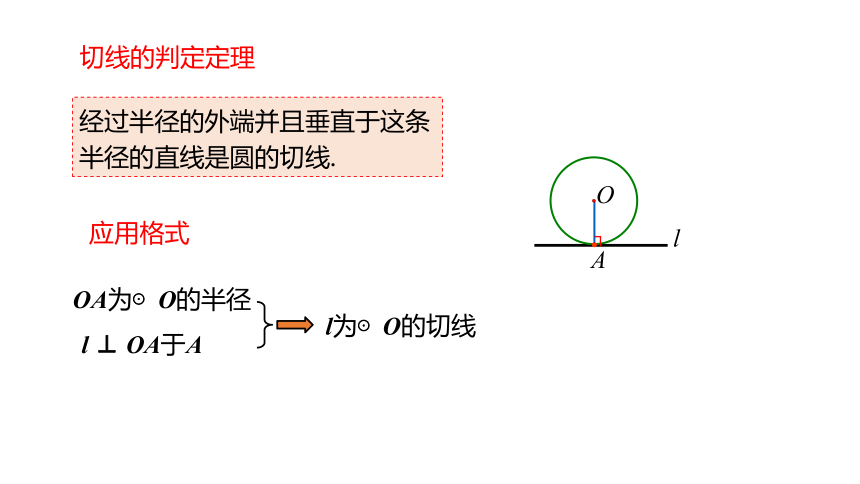
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的判定定理
应用格式
OA为⊙O的半径
l ⊥ OA于A
l为⊙O的切线
l
O
A
┐
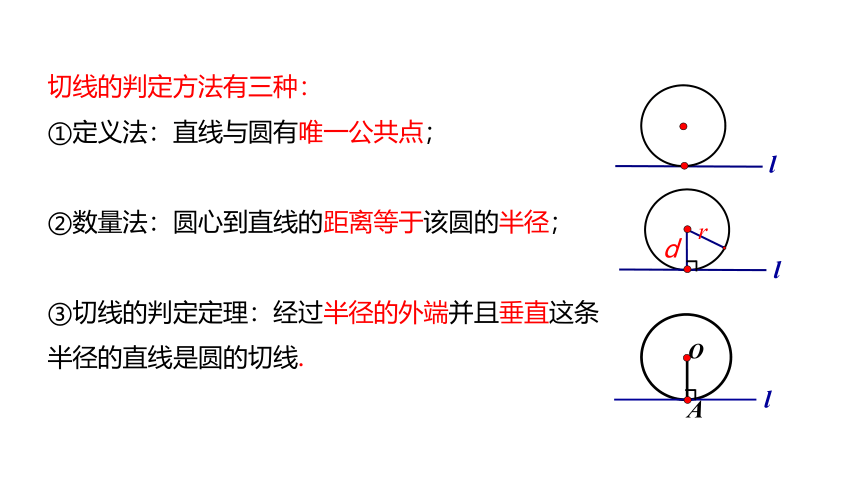
切线的判定方法有三种:
①定义法:直线与圆有唯一公共点;
②数量法:圆心到直线的距离等于该圆的半径;
③切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线.
l
l
r
d
A
l
O
例题讲解
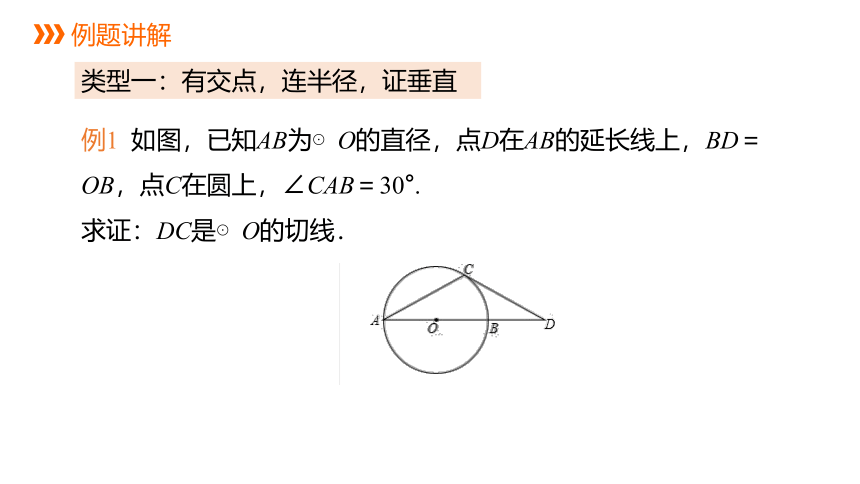
类型一:有交点,连半径,证垂直
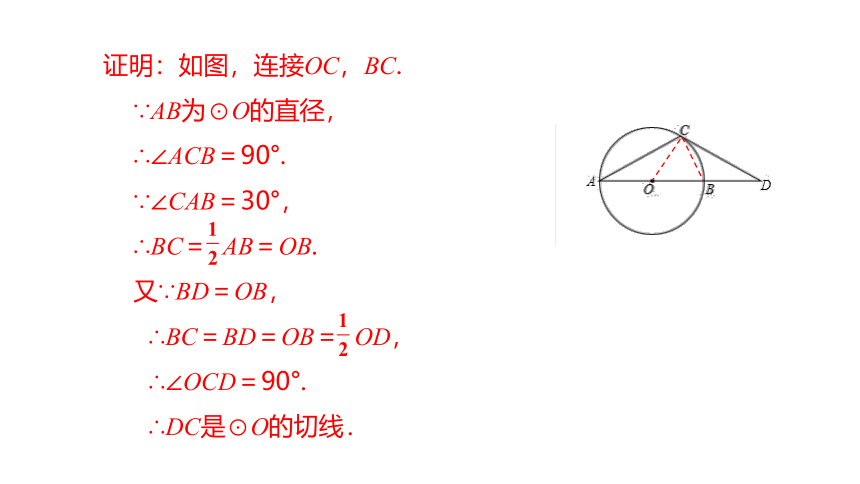
例1 如图,已知AB为⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
证明:如图,连接OC,BC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC= AB=OB.
又∵BD=OB,
∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
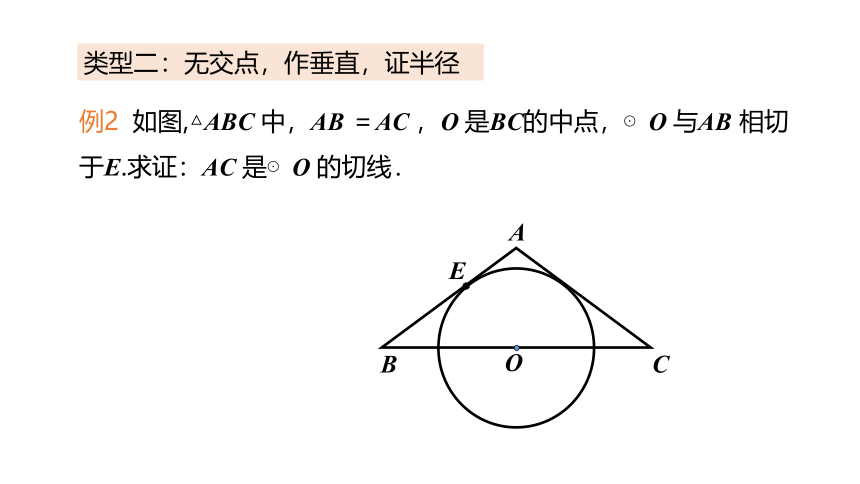
类型二:无交点,作垂直,证半径
例2 如图,△ABC 中,AB =AC ,O 是BC的中点,⊙O 与AB 相切于E.求证:AC 是⊙O 的切线.
B
O
C
E
A
证明:连接OE ,OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E ,
又∵△ABC 中,AB =AC ,O 是BC 的中点.
∴AO 平分∠BAC,
∴OE =OF.
∵OE 是⊙O 半径,OF =OE,OF ⊥ AC.
∴AC 是⊙O 的切线.
又∵OE ⊥AB ,OF⊥AC.
F
B
O
C
E
A
∴OE ⊥ AB.
获取新知
知识点二:三角形的内切圆
如何作圆,使它和已知三角形的各边都相切?
已知:△ABC.
求作:和△ABC的各边都相切的圆I.
分析:如果圆I与△ABC的三条边都相切,那么圆心I到三条边的距离都等于______,从而这些距离相等.
半径
到一个角的两边距离相等的点一定在这个角的平分线上,因此圆心O是∠A 的_______与∠B的_______的___点.
平分线
平分线
交
A
B
C
作法:
1.作∠B和∠C的平分线BM和CN,交点为I.
2.过点I作ID⊥BC.垂足为D.
3.以I为圆心,ID为半径作圆I.
☉I就是所求的圆.
M
N
D
I
A
B
C
与△ABC的三条边都相切的圆有几个?
因为∠B和∠C的平分线的交点只有一个,并且交点O到△ABC三边的距离相等且唯一,所以与△ABC三边都相切的圆有且只有一个.
D
1.与三角形各边都相切的圆叫做三角形的内切圆.
B
2.三角形内切圆的圆心叫做三角形的内心.
4.三角形的内心就是三角形的三条角平分线的交点.
┐
A
C
O
┐
┐
D
E
F
3.三角形的内心到三角形的三边的距离相等.
⊙O是△ABC的内切圆,点O是△ABC的内心.
归纳总结
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边中垂线的交点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条角平分线的交点
1.到三边的距离相等;
2.OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
O
A
B
C
O
议一议
例3 △ABC中,⊙O是△ABC的内切圆,∠A=70°,求∠BOC的度数.
A
B
C
O
解:∵∠A=70°
∴∠ABC+∠ACB=180°-∠A=110°
∵⊙O是△ABC的内切圆
∴BO,CO分别是∠ABC和∠ACB的平分线
即∠OBC= ∠ABC,∠OCB= ∠ACB
例题讲解
例4 如图,点O为∠MPN的平分线上一点,以点O为圆心的⊙O与PN相切于点A. 求证:PM为⊙O的切线.
易错点:判定直线与圆相切时理由不充分.
如图,连接OA,过点O作OB⊥PM于点B.
∵PN与⊙O相切于点A,
∴OA⊥PN.
∵点O在∠MPN的平分线上,
OB⊥PM,
∴OB=OA.
∴点O到直线PM的距离等于⊙O的半径.
∴PM为⊙O的切线.
证明:
随堂演练
1.如图,直线l上有A,B,C,D四点,以点P为圆心,分别以线段PA,PB,PC,PD的长为半径作圆,所得的圆与直线l相切的是( )
A.以PA的长为半径的圆
B.以PB的长为半径的圆
C.以PC的长为半径的圆
D.以PD的长为半径的圆
C
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 .
相切
3. 如图,A,B是☉O上的两点,AC是过点A的一条直线.如果∠AOB=120°,那么当∠CAB的度数为 时,AC才能成为☉O的切线.
60
A
P
O
第4题
4. 如图,D是∠AOB的平分线OC上任意一点,过点D作DE⊥OB于点E,以DE为半径作☉D.求证:OA是☉D的切线.
证明:如图,过点D作DF⊥OA于点F.
∵D是∠AOB的平分线OC上任意一点,DE⊥OB,
∴DF=DE,
即D到直线OA的距离等于☉D的半径DE,
∴OA是☉D的切线.
5.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
课堂小结
第三章 圆
3.6 第2课时 切线的判定
例题讲解
随堂演练
情景导入
获取新知
知识回顾
课堂总结
知识回顾
d r;
d r;
直线和圆相切
直线和圆相离
d r.
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
直线和圆相交
情景引入
砂轮上打磨工件时飞出的火星
下图中让你感受到了直线与圆的哪种位置关系?如何判断一条直线是否为圆的切线呢?
获取新知
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
圆心O到直线l的距离就是OA的长度,也就是r
直线l与⊙O是相切关系
l
O
A
┐
知识点一:切线的判定
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的判定定理
应用格式
OA为⊙O的半径
l ⊥ OA于A
l为⊙O的切线
l
O
A
┐
切线的判定方法有三种:
①定义法:直线与圆有唯一公共点;
②数量法:圆心到直线的距离等于该圆的半径;
③切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线.
l
l
r
d
A
l
O
例题讲解
类型一:有交点,连半径,证垂直
例1 如图,已知AB为⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
证明:如图,连接OC,BC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC= AB=OB.
又∵BD=OB,
∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
类型二:无交点,作垂直,证半径
例2 如图,△ABC 中,AB =AC ,O 是BC的中点,⊙O 与AB 相切于E.求证:AC 是⊙O 的切线.
B
O
C
E
A
证明:连接OE ,OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E ,
又∵△ABC 中,AB =AC ,O 是BC 的中点.
∴AO 平分∠BAC,
∴OE =OF.
∵OE 是⊙O 半径,OF =OE,OF ⊥ AC.
∴AC 是⊙O 的切线.
又∵OE ⊥AB ,OF⊥AC.
F
B
O
C
E
A
∴OE ⊥ AB.
获取新知
知识点二:三角形的内切圆
如何作圆,使它和已知三角形的各边都相切?
已知:△ABC.
求作:和△ABC的各边都相切的圆I.
分析:如果圆I与△ABC的三条边都相切,那么圆心I到三条边的距离都等于______,从而这些距离相等.
半径
到一个角的两边距离相等的点一定在这个角的平分线上,因此圆心O是∠A 的_______与∠B的_______的___点.
平分线
平分线
交
A
B
C
作法:
1.作∠B和∠C的平分线BM和CN,交点为I.
2.过点I作ID⊥BC.垂足为D.
3.以I为圆心,ID为半径作圆I.
☉I就是所求的圆.
M
N
D
I
A
B
C
与△ABC的三条边都相切的圆有几个?
因为∠B和∠C的平分线的交点只有一个,并且交点O到△ABC三边的距离相等且唯一,所以与△ABC三边都相切的圆有且只有一个.
D
1.与三角形各边都相切的圆叫做三角形的内切圆.
B
2.三角形内切圆的圆心叫做三角形的内心.
4.三角形的内心就是三角形的三条角平分线的交点.
┐
A
C
O
┐
┐
D
E
F
3.三角形的内心到三角形的三边的距离相等.
⊙O是△ABC的内切圆,点O是△ABC的内心.
归纳总结
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边中垂线的交点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条角平分线的交点
1.到三边的距离相等;
2.OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
O
A
B
C
O
议一议
例3 △ABC中,⊙O是△ABC的内切圆,∠A=70°,求∠BOC的度数.
A
B
C
O
解:∵∠A=70°
∴∠ABC+∠ACB=180°-∠A=110°
∵⊙O是△ABC的内切圆
∴BO,CO分别是∠ABC和∠ACB的平分线
即∠OBC= ∠ABC,∠OCB= ∠ACB
例题讲解
例4 如图,点O为∠MPN的平分线上一点,以点O为圆心的⊙O与PN相切于点A. 求证:PM为⊙O的切线.
易错点:判定直线与圆相切时理由不充分.
如图,连接OA,过点O作OB⊥PM于点B.
∵PN与⊙O相切于点A,
∴OA⊥PN.
∵点O在∠MPN的平分线上,
OB⊥PM,
∴OB=OA.
∴点O到直线PM的距离等于⊙O的半径.
∴PM为⊙O的切线.
证明:
随堂演练
1.如图,直线l上有A,B,C,D四点,以点P为圆心,分别以线段PA,PB,PC,PD的长为半径作圆,所得的圆与直线l相切的是( )
A.以PA的长为半径的圆
B.以PB的长为半径的圆
C.以PC的长为半径的圆
D.以PD的长为半径的圆
C
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 .
相切
3. 如图,A,B是☉O上的两点,AC是过点A的一条直线.如果∠AOB=120°,那么当∠CAB的度数为 时,AC才能成为☉O的切线.
60
A
P
O
第4题
4. 如图,D是∠AOB的平分线OC上任意一点,过点D作DE⊥OB于点E,以DE为半径作☉D.求证:OA是☉D的切线.
证明:如图,过点D作DF⊥OA于点F.
∵D是∠AOB的平分线OC上任意一点,DE⊥OB,
∴DF=DE,
即D到直线OA的距离等于☉D的半径DE,
∴OA是☉D的切线.
5.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
课堂小结
