北师大版九年级数学下册:3.6 第1课时直线和圆的位置关系及切线的性质课件(共26张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:3.6 第1课时直线和圆的位置关系及切线的性质课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 23:47:00 | ||
图片预览



文档简介
(共26张PPT)
第三章 圆
3.6 第1课时 直线与圆的位置关系及切线的性质
例题讲解
随堂演练
情景导入
获取新知
知识回顾
课堂总结
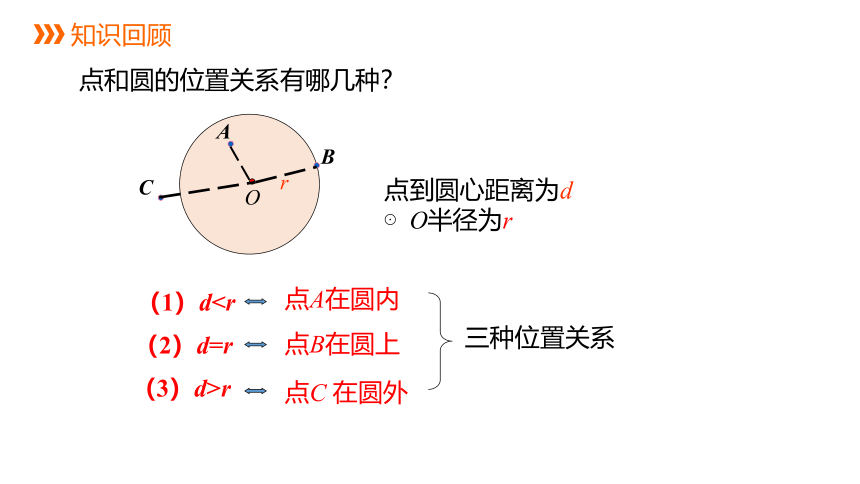
知识回顾
点和圆的位置关系有哪几种?
(1)d(2)d=r
(3)d>r
点A在圆内
点B在圆上
点C 在圆外
三种位置关系
d
A
B
C
O
点到圆心距离为d
⊙O半径为r
r
情景引入
获取新知
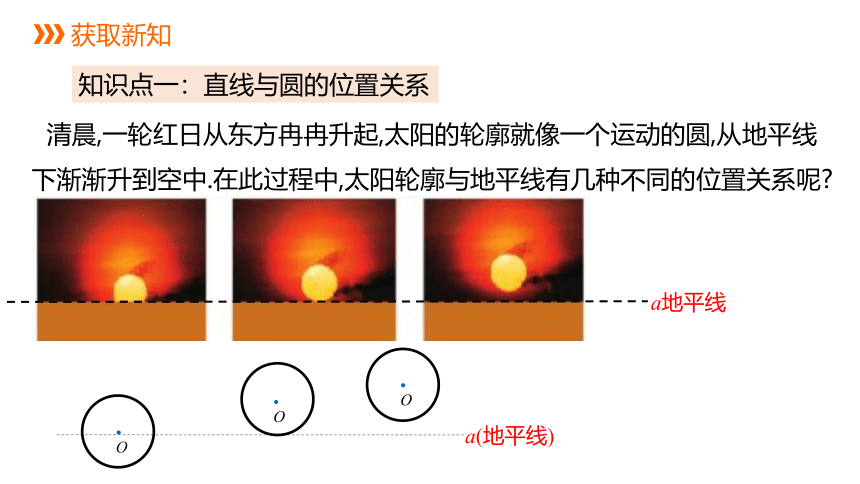
知识点一:直线与圆的位置关系
清晨,一轮红日从东方冉冉升起,太阳的轮廓就像一个运动的圆,从地平线下渐渐升到空中.在此过程中,太阳轮廓与地平线有几种不同的位置关系呢
a地平线
a(地平线)
●O
●O
●O
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺
●O
●O
相交
●O
相切
相离
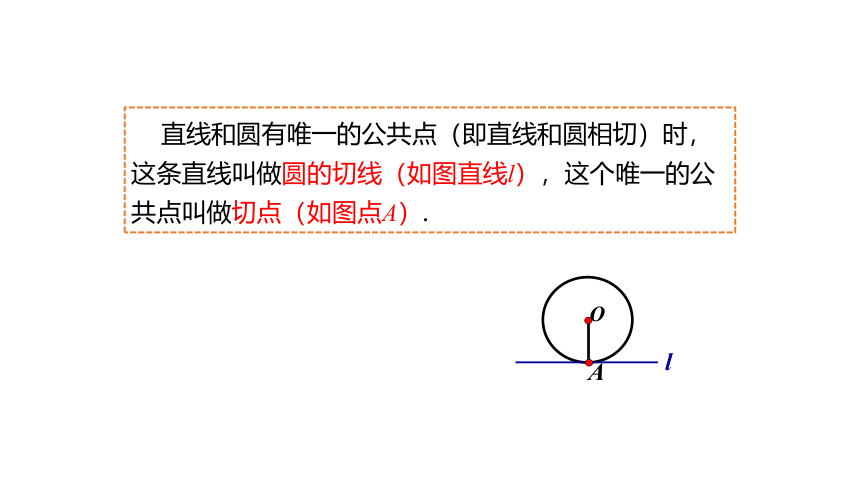
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线l),这个唯一的公共点叫做切点(如图点A).
A
l
O
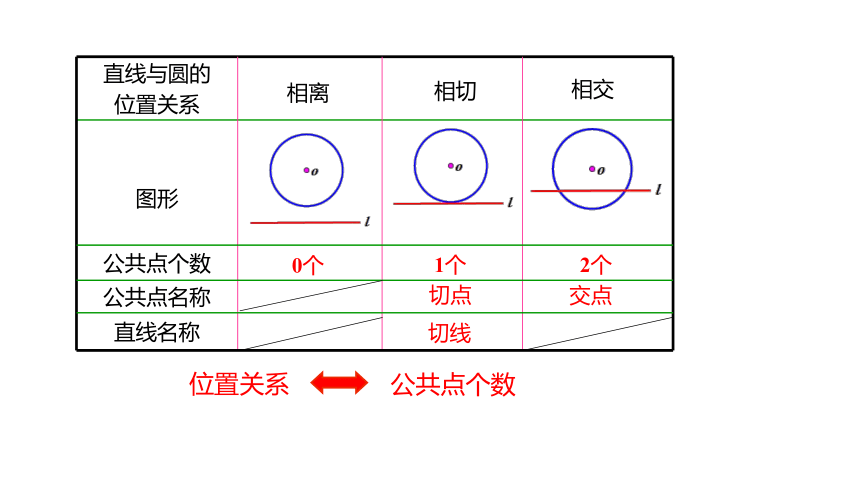
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
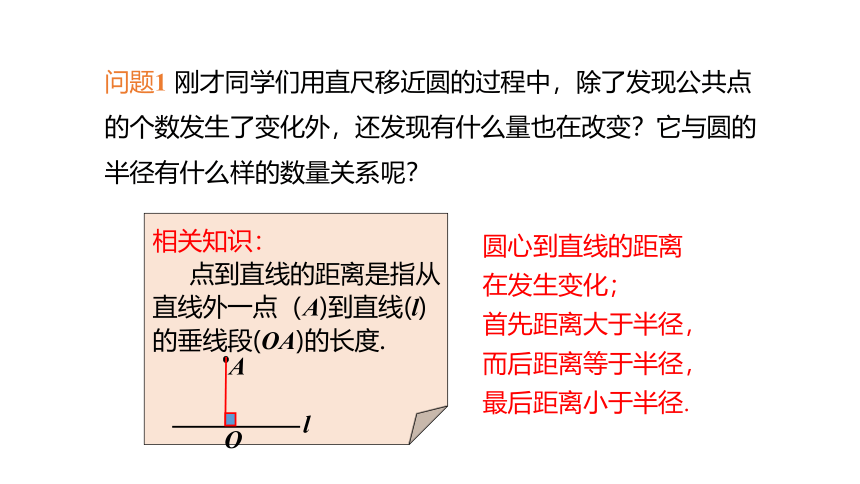
问题1 刚才同学们用直尺移近圆的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
圆心到直线的距离
在发生变化;
首先距离大于半径,
而后距离等于半径,
最后距离小于半径.
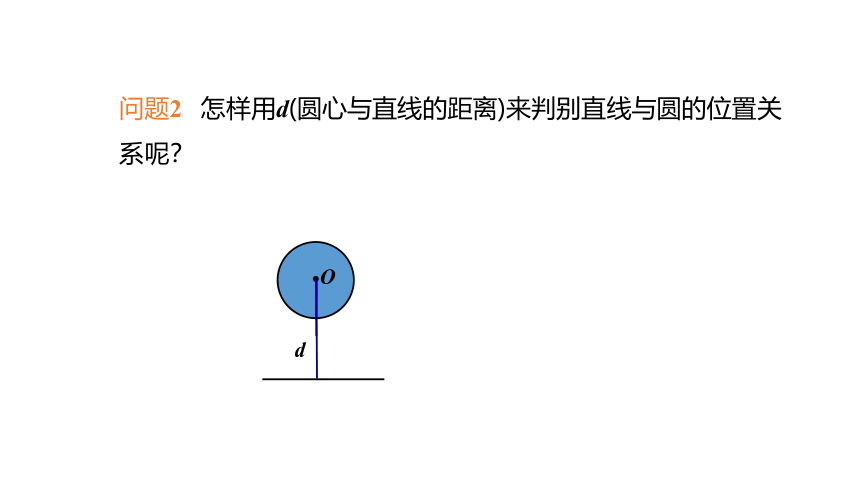
问题2 怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
d>r 直线l与⊙O相离
d=r 直线l与⊙O相切
dd表示圆心O到直线l的距离,
r表示⊙O的半径
r
r
r
数形结合:
位置关系
数量关系
公共点个数
例题讲解
例1 已知 Rt△ABC的斜边 AB= 8 cm, AC= 4 cm.
(1)以点C为圆心作圆,当半径为多长时, AB与⊙O相切?
(2)以点C为圆心,分别以2 cm和4 cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
B
C
A
8
4
解:(1)如图,过点C作AB的垂线,垂足为D.
∵AC = 4cm,AB = 8 cm,
∴cosA=
∴ ∠ A = 60°.
∴ CD = ACsinA = 4 sin 60° = (cm).
因此,当半径长为 cm时,AB与⊙C相切.
B
C
A
D
问题 对于例1(1),你还有其他解法吗?
B
C
A
D
∴
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
根据三角形的面积公式有
因此,当半径长为4.8cm时,AB与圆C相切.
(2)由(1)可知,圆心C到AB的距离 d = cm,所以
当r = 2cm时,d>r, ⊙C与AB相离;
当r = 4cm时,d知识点二:切线的性质
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
C
D
B
●O
A
小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此∠BAC=∠BAD=90°.
获取新知
AB与CD垂直
小亮的理由是:通过反证法.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OM(3)所以AB与CD垂直.
C
D
B
●O
A
M
切线性质
圆的切线垂直于经过切点的半径.
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
应用格式
A
l
O
r
┐
例2 如图,PA为⊙O的切线,切点为A,OP = 2,∠APO=30° ,求⊙O的半径.
解:连接OA,则OA为⊙O的半径,
因为PA是⊙O的切线,所以OA⊥AP,又∠APO=30°,OP=2,
所以OA= OP=1,即⊙O的半径为1.
例题讲解
利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
归纳总结
随堂演练
1. 若直线m与⊙O的公共点个数为2,则直线m与⊙O的位置关系是( )
A.相交 B.相切
C.相交或相切 D.相离
A
2. ☉O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与☉O的位置关系是( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
A
3. 如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则☉C的半径为 ( )
A.2.3 B.2.4 C.2.5 D.2.6
B
4. 如图,C为☉O外一点,CA与☉O相切,切点为A,AB为☉O的直径,连接CB.若☉O的半径为2,∠ABC=60°,则BC= .
8
5. 如图,已知AB为☉O的直径,CD,CB为☉O的两条切线,切点分别为D,B,连接AD.求证:AD//OC.
证明:如图,连接OD.
∵CD,CB为☉O的两条切线,
∴OD⊥CD,OB⊥CB,
∴∠ODC=∠OBC=90°.
又∵OD=OB,OC=OC,
∴Rt△COD≌Rt△COB,
∴∠BOD=2∠BOC.
∵OA=OD,∴∠ODA=∠A.
∵AB为☉O的直径,∠BOD是△AOD的外角,
∴∠BOD=∠ODA+∠A=2∠A.
∴∠BOC=∠A,
∴AD//OC.
课堂小结
第三章 圆
3.6 第1课时 直线与圆的位置关系及切线的性质
例题讲解
随堂演练
情景导入
获取新知
知识回顾
课堂总结
知识回顾
点和圆的位置关系有哪几种?
(1)d
(3)d>r
点A在圆内
点B在圆上
点C 在圆外
三种位置关系
d
A
B
C
O
点到圆心距离为d
⊙O半径为r
r
情景引入
获取新知
知识点一:直线与圆的位置关系
清晨,一轮红日从东方冉冉升起,太阳的轮廓就像一个运动的圆,从地平线下渐渐升到空中.在此过程中,太阳轮廓与地平线有几种不同的位置关系呢
a地平线
a(地平线)
●O
●O
●O
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺
●O
●O
相交
●O
相切
相离
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线l),这个唯一的公共点叫做切点(如图点A).
A
l
O
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
问题1 刚才同学们用直尺移近圆的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
圆心到直线的距离
在发生变化;
首先距离大于半径,
而后距离等于半径,
最后距离小于半径.
问题2 怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
d>r 直线l与⊙O相离
d=r 直线l与⊙O相切
d
r表示⊙O的半径
r
r
r
数形结合:
位置关系
数量关系
公共点个数
例题讲解
例1 已知 Rt△ABC的斜边 AB= 8 cm, AC= 4 cm.
(1)以点C为圆心作圆,当半径为多长时, AB与⊙O相切?
(2)以点C为圆心,分别以2 cm和4 cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
B
C
A
8
4
解:(1)如图,过点C作AB的垂线,垂足为D.
∵AC = 4cm,AB = 8 cm,
∴cosA=
∴ ∠ A = 60°.
∴ CD = ACsinA = 4 sin 60° = (cm).
因此,当半径长为 cm时,AB与⊙C相切.
B
C
A
D
问题 对于例1(1),你还有其他解法吗?
B
C
A
D
∴
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
根据三角形的面积公式有
因此,当半径长为4.8cm时,AB与圆C相切.
(2)由(1)可知,圆心C到AB的距离 d = cm,所以
当r = 2cm时,d>r, ⊙C与AB相离;
当r = 4cm时,d
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
C
D
B
●O
A
小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此∠BAC=∠BAD=90°.
获取新知
AB与CD垂直
小亮的理由是:通过反证法.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OM
C
D
B
●O
A
M
切线性质
圆的切线垂直于经过切点的半径.
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
应用格式
A
l
O
r
┐
例2 如图,PA为⊙O的切线,切点为A,OP = 2,∠APO=30° ,求⊙O的半径.
解:连接OA,则OA为⊙O的半径,
因为PA是⊙O的切线,所以OA⊥AP,又∠APO=30°,OP=2,
所以OA= OP=1,即⊙O的半径为1.
例题讲解
利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
归纳总结
随堂演练
1. 若直线m与⊙O的公共点个数为2,则直线m与⊙O的位置关系是( )
A.相交 B.相切
C.相交或相切 D.相离
A
2. ☉O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与☉O的位置关系是( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
A
3. 如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则☉C的半径为 ( )
A.2.3 B.2.4 C.2.5 D.2.6
B
4. 如图,C为☉O外一点,CA与☉O相切,切点为A,AB为☉O的直径,连接CB.若☉O的半径为2,∠ABC=60°,则BC= .
8
5. 如图,已知AB为☉O的直径,CD,CB为☉O的两条切线,切点分别为D,B,连接AD.求证:AD//OC.
证明:如图,连接OD.
∵CD,CB为☉O的两条切线,
∴OD⊥CD,OB⊥CB,
∴∠ODC=∠OBC=90°.
又∵OD=OB,OC=OC,
∴Rt△COD≌Rt△COB,
∴∠BOD=2∠BOC.
∵OA=OD,∴∠ODA=∠A.
∵AB为☉O的直径,∠BOD是△AOD的外角,
∴∠BOD=∠ODA+∠A=2∠A.
∴∠BOC=∠A,
∴AD//OC.
课堂小结
