九年级数学上第二十五章《概率初步》单元练习题(word版含简单答案)
文档属性
| 名称 | 九年级数学上第二十五章《概率初步》单元练习题(word版含简单答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 156.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览


文档简介
九年级上数学第二十五章《概率初步》单元练习题(含答案)
(总分120分)
第I卷(选择题)
一、单选题(共30分,每小题3分)
1.把一枚均匀的骰子抛掷一次,朝上面的点数为3的概率是( )
A.0 B. C. D.1
2.下列事件中属于必然事件的是( )
A.正数大于负数
B.下周二,温州的天气是阴天
C.在一个只装有白球的袋子中摸出一个红球
D.在一张纸上任意画两条线段,这两条线段相交
3.袋中装有10个黑球、5个红球,1个白球,它们除颜色外无差别,随机从袋子中摸出一球,则下列事件可能性最大的是( )
A.摸到黄球 B.摸到白球 C.摸到红球 D.摸到黑球
4.一枚质地均匀的正六面体骰子六个面分别刻有1到6的点数,掷这枚骰子,前5次朝上的点数恰好是1~5,则第6次朝上的点数是6的可能性( )
A.等于朝上点数为5的可能性
B.大于朝上点数为5的可能性
C.小于朝上点数为5的可能性
D.无法确定
5.一个不透明的箱子中有2个白球,3个黄球和4个红球,这些球除颜色不同外,其他完全相同.从箱子中随机摸出一个球,则它是红球的概率是( )
A. B. C. D.
6.如图,小明周末从家到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( ).
A. B. C. D.0
7.小明同学平时不用功学习,某次数学测验做选择题时,他有1道题不会做,于是随意选了一个答案(每小题4个选项且只有一个选项正确),他选对的概率是( )
A. B. C. D.
8.某校为庆祝中国共产党建党100周年举行“传承红色基因,沐浴阳光成长”歌咏比赛,七年级8个班通过抽签决定出场顺序,七年级(1)班恰好抽到第1个出场的概率为( )
A. B. C. D.
9.在一个不透明的盒子中装有个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是,则黄球的个数为( )
A. B. C. D.
10.一个不透明的袋子里装有黄球18个和红球若干,小明通过多次摸球试验后发现摸到红球的频率稳定在0.4左右,则袋子里有红球( )个
A.12 B.15 C.18 D.24
第II卷(非选择题)
二、填空题(共24分,每小题3分)
11.用图中两个可以自由转动的转盘做“配紫色”游戏.同时转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则同时转动两个转盘可配成紫色的概率是__________.
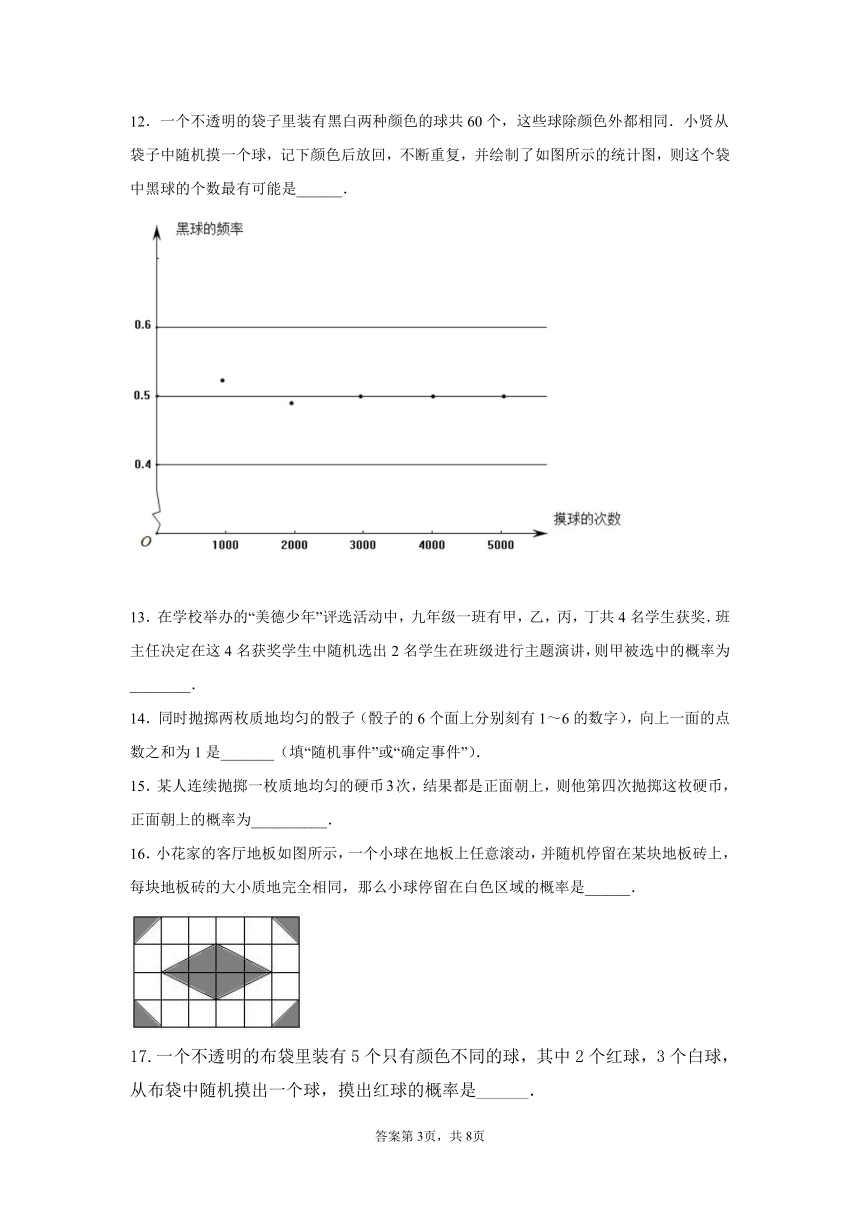
12.一个不透明的袋子里装有黑白两种颜色的球共60个,这些球除颜色外都相同.小贤从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,则这个袋中黑球的个数最有可能是______.
13.在学校举办的“美德少年”评选活动中,九年级一班有甲,乙,丙,丁共4名学生获奖.班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲,则甲被选中的概率为________.
14.同时抛掷两枚质地均匀的骰子(骰子的6个面上分别刻有1~6的数字),向上一面的点数之和为1是_______(填“随机事件”或“确定事件”).
15.某人连续抛掷一枚质地均匀的硬币次,结果都是正面朝上,则他第四次抛掷这枚硬币,正面朝上的概率为__________.
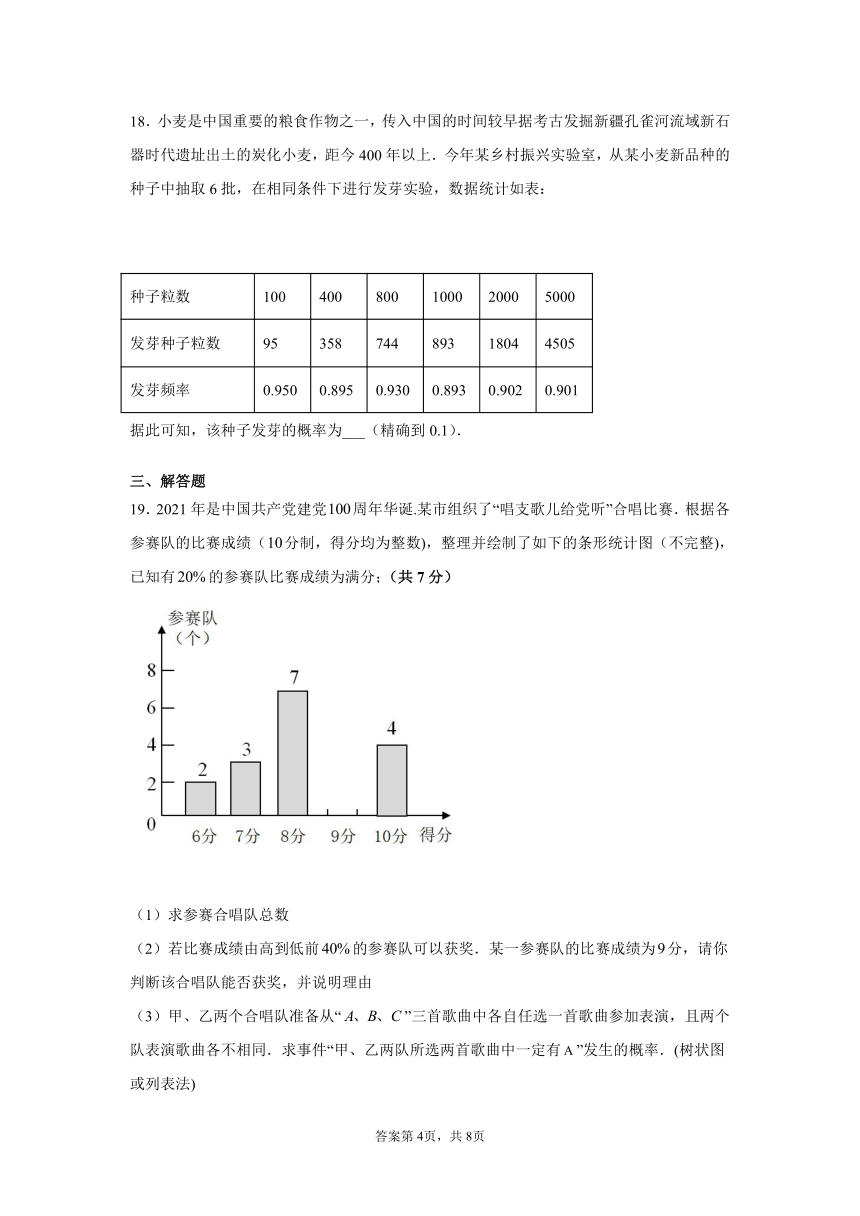
16.小花家的客厅地板如图所示,一个小球在地板上任意滚动,并随机停留在某块地板砖上,每块地板砖的大小质地完全相同,那么小球停留在白色区域的概率是______.
17.一个不透明的布袋里装有5个只有颜色不同的球,其中2个红球,3个白球,从布袋中随机摸出一个球,摸出红球的概率是______.
18.小麦是中国重要的粮食作物之一,传入中国的时间较早据考古发掘新疆孔雀河流域新石器时代遗址出土的炭化小麦,距今400年以上.今年某乡村振兴实验室,从某小麦新品种的种子中抽取6批,在相同条件下进行发芽实验,数据统计如表:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 95 358 744 893 1804 4505
发芽频率 0.950 0.895 0.930 0.893 0.902 0.901
据此可知,该种子发芽的概率为___(精确到0.1).
三、解答题
19.2021年是中国共产党建党周年华诞.某市组织了“唱支歌儿给党听”合唱比赛.根据各参赛队的比赛成绩(分制,得分均为整数),整理并绘制了如下的条形统计图(不完整),已知有的参赛队比赛成绩为满分;(共7分)
(1)求参赛合唱队总数
(2)若比赛成绩由高到低前的参赛队可以获奖.某一参赛队的比赛成绩为分,请你判断该合唱队能否获奖,并说明理由
(3)甲、乙两个合唱队准备从“”三首歌曲中各自任选一首歌曲参加表演,且两个队表演歌曲各不相同.求事件“甲、乙两队所选两首歌曲中一定有”发生的概率.(树状图或列表法)
20.在一个不透明的布袋里装有3个标号为1、2、3的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的2个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).(共7分)
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(x,y)在函数y=﹣x+3图象上的概率.
21.在一个不透明的袋中装有材质、大小完全相同的红球和黑球共100个,小明每次摇匀后随机从袋中摸出一个球,记录颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,估计袋中红球的个数.(共7分)
22.一个口袋中装有7个白球,8个红球,5个黄球,这些球除颜色外完全相同,充分搅匀后随即摸出一球,发现是红球.(共7分)
(1)如果将这个红球放回,再摸出一球,那么摸到红球的概率是多少?
(2)如果将这个红球不放回,再摸出一球,那么它不是红球的概率是多少?
23.在不透明的袋子中有四张标着数字1,2,3,4的卡片.随机抽出一张卡片后不放回,再随机抽出一张卡片,求两次抽到的数字之和为奇数的概率.(共8分)
24.从一副扑克牌中随机抽取一张.(共6分)
(1)它是王牌的概率是多少?
(2)它是Q的概率是多少?
(3)它是梅花的概率是多少?
25.指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是不确定事件? (共8分)
①若 a、b、c都是实数,则a(bc)=(ab)c;
②没有空气,动物也能生存下去;
③在标准大气压下,水在 90℃时沸腾;
④直线 y=k(x+1)过定点(-1,0);
⑤某一天内电话收到的呼叫次数为 0;
⑥一个袋内装有形状大小完全相同的一个白球和一个黑球,从中任意摸出 1个球则为白球.
26.某校教务处为了解九年级学生“居家学习”的学习能力,随机抽取该年级部分学生,对他们的学习能力进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图(其中学习能力指数级别“1”级,代表学习能力很强;“2”级,代表学习能力较强;“3”级,代表学习能力一般;“4“级,代表学习能力较弱)请结合图中相关数据回答问题.(共8分)
(1)本次抽查的学生人数 人,并将条形统计图补充完整;
(2)本次抽查学生“居家学习”能力指数级别的众数为 级,中位数为 级.
(3)已知学习能力很强的学生中只有1名女生,现从中随机抽取两人写有关“居家学习”的报告,请用列表或画树状图的方法求所抽查的两位学生中恰好是一男一女的概率.
27.一个不透明的口袋中装有个红球和个白球,小球除颜色外其余均相同.从口袋中随机摸出一个小球,记下颜色后放回,再随机摸出一个小球.请用画树状图(或列表) 的方法,求两次摸出的小球颜色不同的概率.(共8分)
参考答案
1.C
2.A
3.D
4.A
5.C
6.B
7.A
8.B
9.B
10.A
11.
12.30
13.
14.确定事件
15.
16.
17.2/5
18.0.9
19.(1)20;(2)可以获奖,理由见解析;(3)
20.(1)树状图见解析,共有6种等可能的结果,点P所有可能的坐标为(1,2)、(1,3)、(2,1)、(2,3)、(3,1)、(3,2);(2)
21.85个
22.(1);(2).
23.两次抽到的数字之和为奇数的概率为.
24.(1);(2);(3)
25.①④是必然事件;②③是不可能事件;⑤⑥是不确定事件
26.(1)50,详见解析;(2)3,3;(3).
27.
答案第2页,共8页
答案第1页,共8页
(总分120分)
第I卷(选择题)
一、单选题(共30分,每小题3分)
1.把一枚均匀的骰子抛掷一次,朝上面的点数为3的概率是( )
A.0 B. C. D.1
2.下列事件中属于必然事件的是( )
A.正数大于负数
B.下周二,温州的天气是阴天
C.在一个只装有白球的袋子中摸出一个红球
D.在一张纸上任意画两条线段,这两条线段相交
3.袋中装有10个黑球、5个红球,1个白球,它们除颜色外无差别,随机从袋子中摸出一球,则下列事件可能性最大的是( )
A.摸到黄球 B.摸到白球 C.摸到红球 D.摸到黑球
4.一枚质地均匀的正六面体骰子六个面分别刻有1到6的点数,掷这枚骰子,前5次朝上的点数恰好是1~5,则第6次朝上的点数是6的可能性( )
A.等于朝上点数为5的可能性
B.大于朝上点数为5的可能性
C.小于朝上点数为5的可能性
D.无法确定
5.一个不透明的箱子中有2个白球,3个黄球和4个红球,这些球除颜色不同外,其他完全相同.从箱子中随机摸出一个球,则它是红球的概率是( )
A. B. C. D.
6.如图,小明周末从家到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( ).
A. B. C. D.0
7.小明同学平时不用功学习,某次数学测验做选择题时,他有1道题不会做,于是随意选了一个答案(每小题4个选项且只有一个选项正确),他选对的概率是( )
A. B. C. D.
8.某校为庆祝中国共产党建党100周年举行“传承红色基因,沐浴阳光成长”歌咏比赛,七年级8个班通过抽签决定出场顺序,七年级(1)班恰好抽到第1个出场的概率为( )
A. B. C. D.
9.在一个不透明的盒子中装有个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是,则黄球的个数为( )
A. B. C. D.
10.一个不透明的袋子里装有黄球18个和红球若干,小明通过多次摸球试验后发现摸到红球的频率稳定在0.4左右,则袋子里有红球( )个
A.12 B.15 C.18 D.24
第II卷(非选择题)
二、填空题(共24分,每小题3分)
11.用图中两个可以自由转动的转盘做“配紫色”游戏.同时转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则同时转动两个转盘可配成紫色的概率是__________.
12.一个不透明的袋子里装有黑白两种颜色的球共60个,这些球除颜色外都相同.小贤从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,则这个袋中黑球的个数最有可能是______.
13.在学校举办的“美德少年”评选活动中,九年级一班有甲,乙,丙,丁共4名学生获奖.班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲,则甲被选中的概率为________.
14.同时抛掷两枚质地均匀的骰子(骰子的6个面上分别刻有1~6的数字),向上一面的点数之和为1是_______(填“随机事件”或“确定事件”).
15.某人连续抛掷一枚质地均匀的硬币次,结果都是正面朝上,则他第四次抛掷这枚硬币,正面朝上的概率为__________.
16.小花家的客厅地板如图所示,一个小球在地板上任意滚动,并随机停留在某块地板砖上,每块地板砖的大小质地完全相同,那么小球停留在白色区域的概率是______.
17.一个不透明的布袋里装有5个只有颜色不同的球,其中2个红球,3个白球,从布袋中随机摸出一个球,摸出红球的概率是______.
18.小麦是中国重要的粮食作物之一,传入中国的时间较早据考古发掘新疆孔雀河流域新石器时代遗址出土的炭化小麦,距今400年以上.今年某乡村振兴实验室,从某小麦新品种的种子中抽取6批,在相同条件下进行发芽实验,数据统计如表:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 95 358 744 893 1804 4505
发芽频率 0.950 0.895 0.930 0.893 0.902 0.901
据此可知,该种子发芽的概率为___(精确到0.1).
三、解答题
19.2021年是中国共产党建党周年华诞.某市组织了“唱支歌儿给党听”合唱比赛.根据各参赛队的比赛成绩(分制,得分均为整数),整理并绘制了如下的条形统计图(不完整),已知有的参赛队比赛成绩为满分;(共7分)
(1)求参赛合唱队总数
(2)若比赛成绩由高到低前的参赛队可以获奖.某一参赛队的比赛成绩为分,请你判断该合唱队能否获奖,并说明理由
(3)甲、乙两个合唱队准备从“”三首歌曲中各自任选一首歌曲参加表演,且两个队表演歌曲各不相同.求事件“甲、乙两队所选两首歌曲中一定有”发生的概率.(树状图或列表法)
20.在一个不透明的布袋里装有3个标号为1、2、3的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的2个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).(共7分)
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(x,y)在函数y=﹣x+3图象上的概率.
21.在一个不透明的袋中装有材质、大小完全相同的红球和黑球共100个,小明每次摇匀后随机从袋中摸出一个球,记录颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,估计袋中红球的个数.(共7分)
22.一个口袋中装有7个白球,8个红球,5个黄球,这些球除颜色外完全相同,充分搅匀后随即摸出一球,发现是红球.(共7分)
(1)如果将这个红球放回,再摸出一球,那么摸到红球的概率是多少?
(2)如果将这个红球不放回,再摸出一球,那么它不是红球的概率是多少?
23.在不透明的袋子中有四张标着数字1,2,3,4的卡片.随机抽出一张卡片后不放回,再随机抽出一张卡片,求两次抽到的数字之和为奇数的概率.(共8分)
24.从一副扑克牌中随机抽取一张.(共6分)
(1)它是王牌的概率是多少?
(2)它是Q的概率是多少?
(3)它是梅花的概率是多少?
25.指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是不确定事件? (共8分)
①若 a、b、c都是实数,则a(bc)=(ab)c;
②没有空气,动物也能生存下去;
③在标准大气压下,水在 90℃时沸腾;
④直线 y=k(x+1)过定点(-1,0);
⑤某一天内电话收到的呼叫次数为 0;
⑥一个袋内装有形状大小完全相同的一个白球和一个黑球,从中任意摸出 1个球则为白球.
26.某校教务处为了解九年级学生“居家学习”的学习能力,随机抽取该年级部分学生,对他们的学习能力进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图(其中学习能力指数级别“1”级,代表学习能力很强;“2”级,代表学习能力较强;“3”级,代表学习能力一般;“4“级,代表学习能力较弱)请结合图中相关数据回答问题.(共8分)
(1)本次抽查的学生人数 人,并将条形统计图补充完整;
(2)本次抽查学生“居家学习”能力指数级别的众数为 级,中位数为 级.
(3)已知学习能力很强的学生中只有1名女生,现从中随机抽取两人写有关“居家学习”的报告,请用列表或画树状图的方法求所抽查的两位学生中恰好是一男一女的概率.
27.一个不透明的口袋中装有个红球和个白球,小球除颜色外其余均相同.从口袋中随机摸出一个小球,记下颜色后放回,再随机摸出一个小球.请用画树状图(或列表) 的方法,求两次摸出的小球颜色不同的概率.(共8分)
参考答案
1.C
2.A
3.D
4.A
5.C
6.B
7.A
8.B
9.B
10.A
11.
12.30
13.
14.确定事件
15.
16.
17.2/5
18.0.9
19.(1)20;(2)可以获奖,理由见解析;(3)
20.(1)树状图见解析,共有6种等可能的结果,点P所有可能的坐标为(1,2)、(1,3)、(2,1)、(2,3)、(3,1)、(3,2);(2)
21.85个
22.(1);(2).
23.两次抽到的数字之和为奇数的概率为.
24.(1);(2);(3)
25.①④是必然事件;②③是不可能事件;⑤⑥是不确定事件
26.(1)50,详见解析;(2)3,3;(3).
27.
答案第2页,共8页
答案第1页,共8页
同课章节目录
