沪科版数学七年级上册 4.4 角 课件(共20张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 4.4 角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
4.4 角
你能再举出一些能抽象出角的实例吗?
创设情境,引入新知
自主预习
·
请同学们根据自己对角的认识,画一个角。
观察手中的角的图形,试着说一下在你心目中
什么样的平面图形才是角?
角的描述性定义:
有公共端点的两条射线组成的图形叫做角。
角的顶点
角的两条边
·
试着叙述“平角与周角 ”的形成过程
角的形成性定义:
由一条射线绕着它的端点旋转而形成的图形。
·
始边
终边
O
思考:1、我们把角分成了哪几类?
2、按从大到小的顺序应怎样排列?
3、它们分别有什么特征?
名称: 周角
平角
钝角
直角
锐角
特征: 等于
360度
等于
180度
等于
90度
大于90度
小于180度
大于0度
小于90度
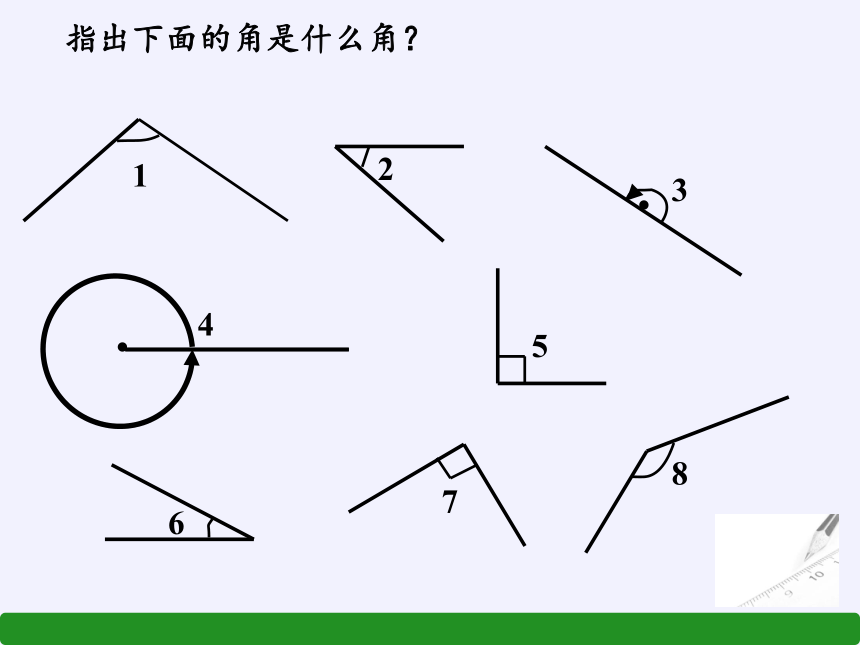
指出下面的角是什么角?
1
2
3
4
5
6
7
8
试着将你手中的角表示出来,
并且思考:
角通常用什么方法表示呢?
自主探究
如图,如何表示这个角?
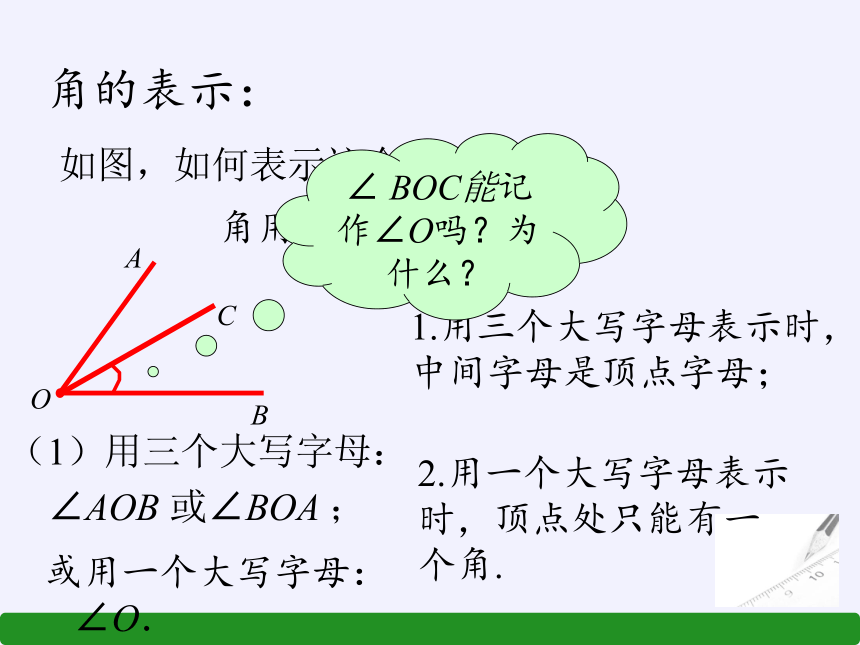
(1)用三个大写字母:
∠AOB 或∠BOA ;
A
O
B
注意:
1.用三个大写字母表示时,中间字母是顶点字母;
2.用一个大写字母表示时,顶点处只能有一个角.
或用一个大写字母:
∠O.
角用符号“∠”来表示.
角的表示:
C
∠ BOC能记作∠O吗?为什么?
角的表示:
(2)用一个数字加弧线表示:
1
α
(3)用一个小写希腊字母加弧线表示:
∠1
∠α
注意:
这两种方法必须在图上标注后才能使用,并且只能表示单独的一个角.
A
O
B
C
1
能把∠ AOB记作∠ 1吗?为什么?
我会判断!
1、一条射线比一条直线短。 ( )
2、一条射线长100米。 ( )
3、角的两条边都是射线。 ( )
4、角的两条边越长,角的度数越大。( )
5、有端点的线就是线段 。 ( )
6、用直尺可以度量线段的长度,用量角器可以度量角的大小。 ( )
×
×
√
×
×
√
把一个周角360等分,每一份就是1度的角,记做1°.除了“度”之外,还有其它的度量单位吗?
1°的60分之一为1分,记作1′,即1°=60′
1′的60分之一为1秒,记作1″,即1′=60″
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.
如图,已知∠AOB,用量角器量出它的度数.
A
O
B
1.对中——角的顶点对量角器的中心;
3.读数——读出角的另一边所对的度数.
2.重合——角的一边与量角器的零线重合;
用量角器度量角的方法:
例1 计算:
(1)用度、分、秒表示30.26
(2)42 18‘15“等于多少度?
例2 把一个周角17等分,每份是多少?
(精确到1')
自主探究
1. 判断下面各角的表示方法是否正确.
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
∠ACB
∠B
∠ABC
∠CAB
∠A
( )
( )
( )
( )
( )
×
×
×
√
√
2. 下面表示∠DEF的图是( )
E
D
E
F
(1)
E
D
F
(2)
D
E
F
(3)
D
E
F
(4)
(3)
随堂练习
3.如图,点O是直线AB上任意一点,OC、OD、OE是三条射线,图中共有几个小于平角的角?
9个
1). 1小时= 分, 1分= 秒.
2). 3.3小时= 小时 分,
2小时30分= 小时.
3). 1°= ′,1′= ″.
4). 0.75°= ′= ″,
34.37°= ° ′ ″.
5). 1800″= °,39°36′= °.
60
60
3
18
2.5
60
60
45
34
22
12
0.5
39.6
2700
4.填一填:
经常不断地学习,你就什么都知道。 你知道得越多,你就越有力量。
———— 高尔基
结束语
谢 谢
4.4 角
你能再举出一些能抽象出角的实例吗?
创设情境,引入新知
自主预习
·
请同学们根据自己对角的认识,画一个角。
观察手中的角的图形,试着说一下在你心目中
什么样的平面图形才是角?
角的描述性定义:
有公共端点的两条射线组成的图形叫做角。
角的顶点
角的两条边
·
试着叙述“平角与周角 ”的形成过程
角的形成性定义:
由一条射线绕着它的端点旋转而形成的图形。
·
始边
终边
O
思考:1、我们把角分成了哪几类?
2、按从大到小的顺序应怎样排列?
3、它们分别有什么特征?
名称: 周角
平角
钝角
直角
锐角
特征: 等于
360度
等于
180度
等于
90度
大于90度
小于180度
大于0度
小于90度
指出下面的角是什么角?
1
2
3
4
5
6
7
8
试着将你手中的角表示出来,
并且思考:
角通常用什么方法表示呢?
自主探究
如图,如何表示这个角?
(1)用三个大写字母:
∠AOB 或∠BOA ;
A
O
B
注意:
1.用三个大写字母表示时,中间字母是顶点字母;
2.用一个大写字母表示时,顶点处只能有一个角.
或用一个大写字母:
∠O.
角用符号“∠”来表示.
角的表示:
C
∠ BOC能记作∠O吗?为什么?
角的表示:
(2)用一个数字加弧线表示:
1
α
(3)用一个小写希腊字母加弧线表示:
∠1
∠α
注意:
这两种方法必须在图上标注后才能使用,并且只能表示单独的一个角.
A
O
B
C
1
能把∠ AOB记作∠ 1吗?为什么?
我会判断!
1、一条射线比一条直线短。 ( )
2、一条射线长100米。 ( )
3、角的两条边都是射线。 ( )
4、角的两条边越长,角的度数越大。( )
5、有端点的线就是线段 。 ( )
6、用直尺可以度量线段的长度,用量角器可以度量角的大小。 ( )
×
×
√
×
×
√
把一个周角360等分,每一份就是1度的角,记做1°.除了“度”之外,还有其它的度量单位吗?
1°的60分之一为1分,记作1′,即1°=60′
1′的60分之一为1秒,记作1″,即1′=60″
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.
如图,已知∠AOB,用量角器量出它的度数.
A
O
B
1.对中——角的顶点对量角器的中心;
3.读数——读出角的另一边所对的度数.
2.重合——角的一边与量角器的零线重合;
用量角器度量角的方法:
例1 计算:
(1)用度、分、秒表示30.26
(2)42 18‘15“等于多少度?
例2 把一个周角17等分,每份是多少?
(精确到1')
自主探究
1. 判断下面各角的表示方法是否正确.
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
∠ACB
∠B
∠ABC
∠CAB
∠A
( )
( )
( )
( )
( )
×
×
×
√
√
2. 下面表示∠DEF的图是( )
E
D
E
F
(1)
E
D
F
(2)
D
E
F
(3)
D
E
F
(4)
(3)
随堂练习
3.如图,点O是直线AB上任意一点,OC、OD、OE是三条射线,图中共有几个小于平角的角?
9个
1). 1小时= 分, 1分= 秒.
2). 3.3小时= 小时 分,
2小时30分= 小时.
3). 1°= ′,1′= ″.
4). 0.75°= ′= ″,
34.37°= ° ′ ″.
5). 1800″= °,39°36′= °.
60
60
3
18
2.5
60
60
45
34
22
12
0.5
39.6
2700
4.填一填:
经常不断地学习,你就什么都知道。 你知道得越多,你就越有力量。
———— 高尔基
结束语
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
