2022年广东高中数学学业水平考试模拟卷三(Word含答案解析)
文档属性
| 名称 | 2022年广东高中数学学业水平考试模拟卷三(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 537.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 11:13:47 | ||
图片预览




文档简介
2022年广东高中数学学业水平考试模拟卷三
学校:___________姓名:___________班级:___________成绩:___________
选择题:在每小题给出的四个选项中,只有一个选项是符合题目要求的,每小题6分,共90分。
1.已知集合A=,B=,则=( )
A.{1,3} B.{1,3,5} C.{1,3,5,7} D.
2.下列等式成立的是( )
A. B.
C. D.
3.设, ,, 则( )
A.cC.c4.为了得到函数的图象,只要把函数图象上所有的点( )
A.向右平行移动个单位长度
B.向左平行移动个单位长度
C.向右平行移动个单位长度
D.向左平行移动个单位长度
5.设用二分法求方程在区间上近似解的过程中,计算得到,则方程的根落在区间( )
A. B. C. D.
6.如图,在矩形ABCD中,,将矩形ABCD绕边AB所在直线旋转一周形成一个圆柱,则该圆柱的体积为( )
A.3π B.6π C.12π D.16π
7.如图,在四面体ABCD中,E,F分别是AC与BD的中点,若CD=2AB=4,EF⊥BA,则EF与CD所成的角为( )
A.90° B.45° C.60° D.30°
8.下列事件:
①如果,那么.
②某人射击一次,命中靶心.
③任取一实数(且),函数是增函数,
④从盛有一红、二白共三个球的袋子中,摸出一球观察结果是黄球.
其中是随机事件的为
A.①② B.③④ C.①④ D.②③
9.设是两条不同的直线,是三个不同的平面,则下列命题为真命题的是( )
A.若,,则
B.若,则
C.若,则
D.若,则
10.如图在边长为1的正方形组成的网格中,平行四边形ABCD的顶点D被阴影遮住,则=( )
A.10 B.11 C.12 D.13
11.某学校有160名教职工,其中教师120名,行政人员16名,后勤服务人员24名,今从中抽取一个容量为20的样本,采用( )较为合适.
A.简单随机抽样 B.系统抽样
C.分层抽样 D.其他抽样
12.下列说法中,正确的是( )
A.每一条直线都有倾斜角和斜率
B.若直线倾斜角为,则斜率为
C.若两直线的斜率,满足,则两直线互相垂直
D.直线与直线()一定互相平行
13.已知某学校高二年级的一班和二班分别有人和人.某次学校考试中,两班学生的平均分分别为和,则这两个班学生的数学平均分为( )
A. B.
C. D.
14.据人口普查统计,育龄妇女生男生女是等可能的,如果允许生育二胎,则某一育龄妇女两胎均
是女孩的概率是
A. B. C. D.
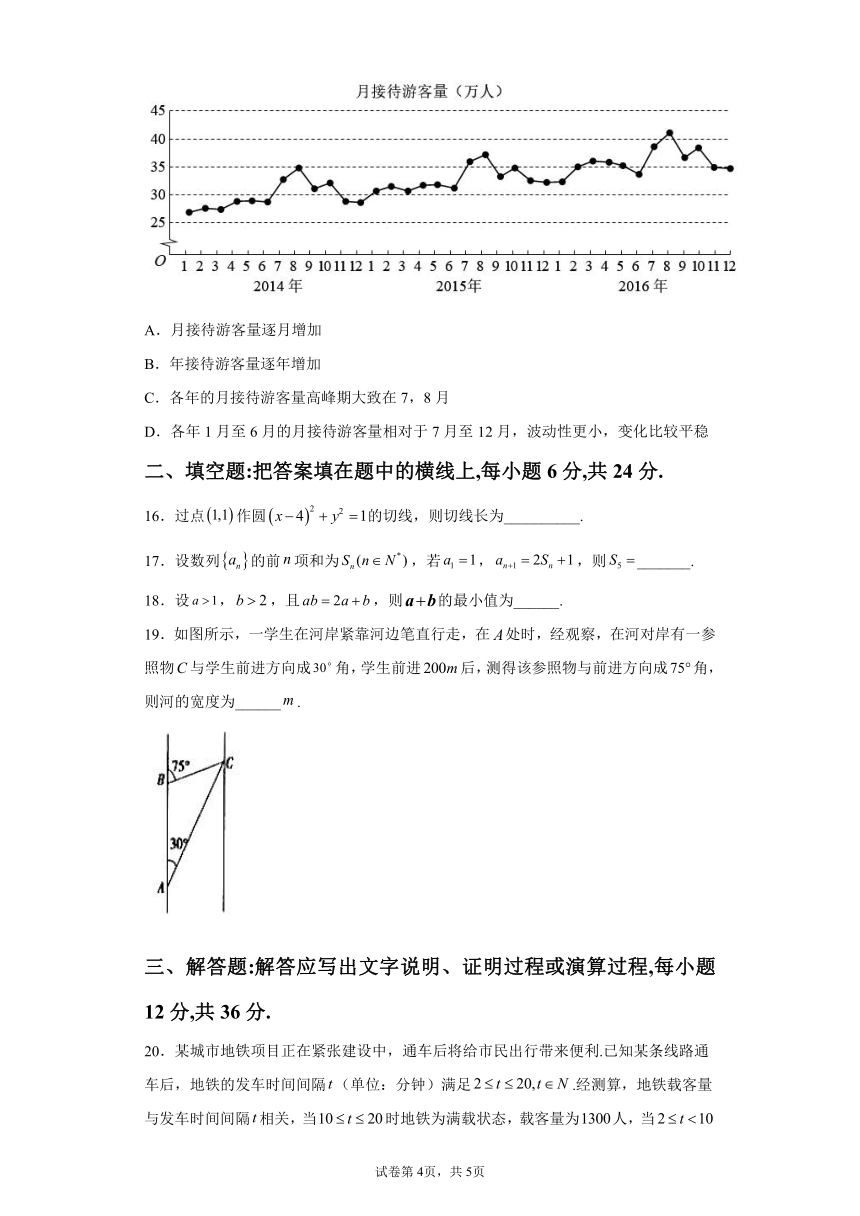
15.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
二、填空题:把答案填在题中的横线上,每小题6分,共24分.
16.过点作圆的切线,则切线长为__________.
17.设数列的前项和为,若,,则_______.
18.设,,且,则的最小值为______.
19.如图所示,一学生在河岸紧靠河边笔直行走,在处时,经观察,在河对岸有一参照物与学生前进方向成角,学生前进后,测得该参照物与前进方向成角,则河的宽度为______.
三、解答题:解答应写出文字说明、证明过程或演算过程,每小题12分,共36分.
20.某城市地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔(单位:分钟)满足.经测算,地铁载客量与发车时间间隔相关,当时地铁为满载状态,载客量为人,当时,载客量会减少,减少的人数与的平方成正比,且发车时间间隔为分钟时的载客量为人,记地铁载客量为.
(1)求的表达式,并求当发车时间间隔为分钟时,地铁的载客量;
(2)若该线路每分钟的净收益为(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?每分钟的最大净收益为多少?
21.已知a,b,c分别为锐角三角形三个内角A,B,C的对边,且.
(1)求A;
(2)若,的面积为,求b,c.
22.如图,三棱柱ABC- A1B1C1的底面是边长为2的正三角形,侧棱BB1⊥底面ABC,BB1=2,D,E分别为CC1, AA1的中点.
(1)求证∶ CE //平面BDA1;
(2)求四棱锥B-CAA1D的体积.
试卷第1页,共3页
试卷第1页,共3页
2022年广东高中数学学业水平考试模拟卷三
参考答案
1.A
【分析】
根据集合的交集定义得到答案.
【详解】
集合B中只有1,3满足集合A中的条件,
∴={1,3},
故选:.
2.C
【分析】
根据对数的运算法则逐一判断可得选项.
【详解】
对于A:,故A不正确;
对于B:,故B不正确;
对于C:∵,∴,故C正确,
对于D:,故D不正确,
故选: C.
3.B
【分析】
根据指数函数与对数函数单调性,结合中间值比较即可.
【详解】
解:因为,,,
所以
故选:B
4.C
【分析】
根据三角图象变换的法则即可求出.
【详解】
因为,所以只要把函数图象上所有的点向右平行移动个单位长度,即可得到函数的图象.
故选:C
5.B
【分析】
利用零点存在性定理求解.
【详解】
函数在单调递增,又因为,
所以由零点存在性定理知,在区间上有零点,
即在区间上的根落在区间上.
故选:B.
6.C
【分析】
根据题意得到圆柱的底面半径和高,结合体积公式,即可求解.
【详解】
由题意,矩形中,,
即圆柱的底面圆的半径为,高为,
所以圆柱的体积为.
故选:C.
7.D
【分析】
设G为AD的中点,连接GF,GE,由三角形中位线定理可得,,则∠GFE即为EF与CD所成的角,结合AB=2,CD=4,EF⊥AB,在△GEF中,利用三角函数即可得到答案.
【详解】
解:设G为AD的中点,连接GF,GE
则GF,GE分别为△ABD,△ACD的中线.
∴ ,且,,且,则EF与CD所成角的度数等于EF与GE所成角的度数
又EF⊥ AB,
∴ EF⊥ GF
则△GEF为直角三角形,GF=1,GE=2,∠GFE=90°
∴ 在直角△GEF中,
∴ ∠GEF=30°.
故选:D.
8.D
【详解】
是必然事件;
中时,单调递增,时,为减函数,故是随机事件;
是随机事件;
是不可能事件
故答案选
9.C
【分析】
根据线面位置关系依次讨论各选项即可得答案.
【详解】
对于A选项,若,,则或异面,故A选项错误;
对于B选项,若,则或相交,故B选项错误;
对于C选项,由得,所以当时,,故C选项正确;
对于D选项,若且时,,故D选项错误;
故选:C
10.B
【分析】
以A为坐标原点,建立平面直角坐标系,利用向量数量积的坐标运算即可求解.
【详解】
以A为坐标原点,建立平面直角坐标系,
则A(0,0),B(4,1),C(6,4),
=(4,1),=(2,3),
=4×2+1×3=11,
故选:B.
【点睛】
本题考查了向量数量积的坐标运算,考查了基本运算能力,属于基础题.
11.C
【分析】
利用分层抽样的概念求解.
【详解】
由题知,学校教职工有3种类别,所以选用分层抽样较为合适.
故选:C.
12.C
【分析】
根据直线的倾斜角与斜率的定义及关系,以及两直线的位置的判定方法,逐项判定,即可求解.
【详解】
对于A中,每条直线都有倾斜角,当倾斜角为,直线的斜率不存在,所以A错误;
对于B中,当直线倾斜角为,此时直线的斜率不存在,所以B错误;
对于C中,若两直线的斜率分别为,,当,则两直线互相垂直,所以C正确;
对于D中,当时,直线与直线为重合直线,所以D错误.
故选:C.
13.C
【分析】
利用平均数公式可求得结果.
【详解】
这两个班学生的数学总分为,故这两个班学生的数学平均分为.
故选:C.
14.C
【解析】
试题分析:所有基本事件有:,两胎均是女孩的基本事件只有,两胎均是女孩的概率,故选C.
考点:古典概型.
15.A
【分析】
观察折线图,结合选项逐一判断即可
【详解】
对于选项A,由图易知月接待游客量每年7,8月份明显高于12月份,故A错;
对于选项B,观察折线图的变化趋势可知年接待游客量逐年增加,故B正确;
对于选项C,观察折线图,各年的月接待游客量高峰期大致在7,8月份,故C正确;
对于D选项,观察折线图,各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳,故D正确.
故选:A
16.
【分析】
求出圆心与点的距离,再利用勾股定理即可得出答案.
【详解】
解:圆的圆心为,半径,
则圆心与点的距离,
所以切线长为.
故答案为:.
17..
【解析】
试题分析:由题意得,,
∴是以为首项,为公比的等比数列,∴,故填:.
考点:数列的通项公式及其运算.
18.
【分析】
将等式变形为,由此得出,展开后利用基本不等式可得出的最小值.
【详解】
在等式两边同时除以得,
,,,
当且仅当时,等号成立,
因此,的最小值为.
故答案为:.
【点睛】
本题考查利用基本不等式求最值,涉及的妙用,解题时将注意将定值条件化简变形,考查计算能力,属于中等题.
19..
【分析】
先在中用正弦定理求出,然后河的宽度为
【详解】
由题意可得在中,,且
所以由正弦定理得:
则
所以河的宽度为:
故答案为:
【点睛】
本题考查的是运用正弦定理解三角形,较简单.
20.(1),人(2)当发车时间间隔为分钟时,该线路每分钟的净收益最大,每分钟的最大净收益为元
【分析】
(1)由题意分别写出与时,的表达式,写成分段函数的形式,可得的表达式,可得的值;
(2)分别求出时,时,净收益为的表达式,并求出其最大值,进行比较可得净收益最大及收益最大时的时间.
【详解】
解:当时,
当时,设
解得,所以,
所以
(人)
当时,
当时
当时,
当且仅当时,即时, 取到最大值.
答:的表达式为
当发车时间间隔为分钟时,地铁的载客量为人.
当发车时间间隔为分钟时,该线路每分钟的净收益最大,每分钟的最大净收益为元.
【点睛】
本题主要考查分段函数解析式的求解及函数模型的实际应用,及利用基本不等式求解函数的最值,综合性大,属于中档题.
21.(1);(2).
【分析】
(1)由正弦定理可得,消去,可得,可得答案;
(2)由(1)所求A及,可得的值,再由余弦定理,可得b,c的值.
【详解】
解:(1)因为,
由正弦定理得:,
因为,所以.
因为A为锐角,所以.
(2)由,得:.
又的面积为,即.
所以.则.解得.
【点睛】
本题主要考查利用正弦定理、余弦定理解三角形,需注意公式的灵活运用.
22.(1)证明见解析;(2).
【分析】
(1)先证明CE //DA1,再利用线面平行的判定定理即可证明;
(2)利用线面垂直的判定定理的判定定理证明BF⊥平面CAA1D,然后求出直角梯形CAA1D的面积,利用锥体体积公式即可求解.
【详解】
(1)在三棱柱中,AA1 //CC1,AA1= CC1
因为D,E分别是CC1, AA1的中点,
所以CD//EA1,CD= EA1
所以四边形CEA1D是平行四边形.
所以CE //DA1
又因为CE平面BDA1,DA1 平面BDA1
所以CE//平面BDA1.
(2)设F为AC的中点,又△ABC为正三角形,
所以BF⊥AC.
在三棱柱ABC-A1B1C1中,AA1//BB1.
因为BB⊥平面ABC,所以AA1⊥平面ABC.
又BF平面ABC
所以AA1⊥BF.
又BF⊥AC,AA1∩AC=A
所以BF⊥平面CAA1D .
因此BF是四棱锥B-CAA1D的高,
因为正△ABC的边长为2,所以.
在三棱柱中,,
又D是CC1的中点,所以CD=1.
于是直角梯形CAA1D的面积
所以
所以四棱锥B-CAA1D的体试卷第1页,共3页
试卷第1页,共3页
学校:___________姓名:___________班级:___________成绩:___________
选择题:在每小题给出的四个选项中,只有一个选项是符合题目要求的,每小题6分,共90分。
1.已知集合A=,B=,则=( )
A.{1,3} B.{1,3,5} C.{1,3,5,7} D.
2.下列等式成立的是( )
A. B.
C. D.
3.设, ,, 则( )
A.c
A.向右平行移动个单位长度
B.向左平行移动个单位长度
C.向右平行移动个单位长度
D.向左平行移动个单位长度
5.设用二分法求方程在区间上近似解的过程中,计算得到,则方程的根落在区间( )
A. B. C. D.
6.如图,在矩形ABCD中,,将矩形ABCD绕边AB所在直线旋转一周形成一个圆柱,则该圆柱的体积为( )
A.3π B.6π C.12π D.16π
7.如图,在四面体ABCD中,E,F分别是AC与BD的中点,若CD=2AB=4,EF⊥BA,则EF与CD所成的角为( )
A.90° B.45° C.60° D.30°
8.下列事件:
①如果,那么.
②某人射击一次,命中靶心.
③任取一实数(且),函数是增函数,
④从盛有一红、二白共三个球的袋子中,摸出一球观察结果是黄球.
其中是随机事件的为
A.①② B.③④ C.①④ D.②③
9.设是两条不同的直线,是三个不同的平面,则下列命题为真命题的是( )
A.若,,则
B.若,则
C.若,则
D.若,则
10.如图在边长为1的正方形组成的网格中,平行四边形ABCD的顶点D被阴影遮住,则=( )
A.10 B.11 C.12 D.13
11.某学校有160名教职工,其中教师120名,行政人员16名,后勤服务人员24名,今从中抽取一个容量为20的样本,采用( )较为合适.
A.简单随机抽样 B.系统抽样
C.分层抽样 D.其他抽样
12.下列说法中,正确的是( )
A.每一条直线都有倾斜角和斜率
B.若直线倾斜角为,则斜率为
C.若两直线的斜率,满足,则两直线互相垂直
D.直线与直线()一定互相平行
13.已知某学校高二年级的一班和二班分别有人和人.某次学校考试中,两班学生的平均分分别为和,则这两个班学生的数学平均分为( )
A. B.
C. D.
14.据人口普查统计,育龄妇女生男生女是等可能的,如果允许生育二胎,则某一育龄妇女两胎均
是女孩的概率是
A. B. C. D.
15.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
二、填空题:把答案填在题中的横线上,每小题6分,共24分.
16.过点作圆的切线,则切线长为__________.
17.设数列的前项和为,若,,则_______.
18.设,,且,则的最小值为______.
19.如图所示,一学生在河岸紧靠河边笔直行走,在处时,经观察,在河对岸有一参照物与学生前进方向成角,学生前进后,测得该参照物与前进方向成角,则河的宽度为______.
三、解答题:解答应写出文字说明、证明过程或演算过程,每小题12分,共36分.
20.某城市地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔(单位:分钟)满足.经测算,地铁载客量与发车时间间隔相关,当时地铁为满载状态,载客量为人,当时,载客量会减少,减少的人数与的平方成正比,且发车时间间隔为分钟时的载客量为人,记地铁载客量为.
(1)求的表达式,并求当发车时间间隔为分钟时,地铁的载客量;
(2)若该线路每分钟的净收益为(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?每分钟的最大净收益为多少?
21.已知a,b,c分别为锐角三角形三个内角A,B,C的对边,且.
(1)求A;
(2)若,的面积为,求b,c.
22.如图,三棱柱ABC- A1B1C1的底面是边长为2的正三角形,侧棱BB1⊥底面ABC,BB1=2,D,E分别为CC1, AA1的中点.
(1)求证∶ CE //平面BDA1;
(2)求四棱锥B-CAA1D的体积.
试卷第1页,共3页
试卷第1页,共3页
2022年广东高中数学学业水平考试模拟卷三
参考答案
1.A
【分析】
根据集合的交集定义得到答案.
【详解】
集合B中只有1,3满足集合A中的条件,
∴={1,3},
故选:.
2.C
【分析】
根据对数的运算法则逐一判断可得选项.
【详解】
对于A:,故A不正确;
对于B:,故B不正确;
对于C:∵,∴,故C正确,
对于D:,故D不正确,
故选: C.
3.B
【分析】
根据指数函数与对数函数单调性,结合中间值比较即可.
【详解】
解:因为,,,
所以
故选:B
4.C
【分析】
根据三角图象变换的法则即可求出.
【详解】
因为,所以只要把函数图象上所有的点向右平行移动个单位长度,即可得到函数的图象.
故选:C
5.B
【分析】
利用零点存在性定理求解.
【详解】
函数在单调递增,又因为,
所以由零点存在性定理知,在区间上有零点,
即在区间上的根落在区间上.
故选:B.
6.C
【分析】
根据题意得到圆柱的底面半径和高,结合体积公式,即可求解.
【详解】
由题意,矩形中,,
即圆柱的底面圆的半径为,高为,
所以圆柱的体积为.
故选:C.
7.D
【分析】
设G为AD的中点,连接GF,GE,由三角形中位线定理可得,,则∠GFE即为EF与CD所成的角,结合AB=2,CD=4,EF⊥AB,在△GEF中,利用三角函数即可得到答案.
【详解】
解:设G为AD的中点,连接GF,GE
则GF,GE分别为△ABD,△ACD的中线.
∴ ,且,,且,则EF与CD所成角的度数等于EF与GE所成角的度数
又EF⊥ AB,
∴ EF⊥ GF
则△GEF为直角三角形,GF=1,GE=2,∠GFE=90°
∴ 在直角△GEF中,
∴ ∠GEF=30°.
故选:D.
8.D
【详解】
是必然事件;
中时,单调递增,时,为减函数,故是随机事件;
是随机事件;
是不可能事件
故答案选
9.C
【分析】
根据线面位置关系依次讨论各选项即可得答案.
【详解】
对于A选项,若,,则或异面,故A选项错误;
对于B选项,若,则或相交,故B选项错误;
对于C选项,由得,所以当时,,故C选项正确;
对于D选项,若且时,,故D选项错误;
故选:C
10.B
【分析】
以A为坐标原点,建立平面直角坐标系,利用向量数量积的坐标运算即可求解.
【详解】
以A为坐标原点,建立平面直角坐标系,
则A(0,0),B(4,1),C(6,4),
=(4,1),=(2,3),
=4×2+1×3=11,
故选:B.
【点睛】
本题考查了向量数量积的坐标运算,考查了基本运算能力,属于基础题.
11.C
【分析】
利用分层抽样的概念求解.
【详解】
由题知,学校教职工有3种类别,所以选用分层抽样较为合适.
故选:C.
12.C
【分析】
根据直线的倾斜角与斜率的定义及关系,以及两直线的位置的判定方法,逐项判定,即可求解.
【详解】
对于A中,每条直线都有倾斜角,当倾斜角为,直线的斜率不存在,所以A错误;
对于B中,当直线倾斜角为,此时直线的斜率不存在,所以B错误;
对于C中,若两直线的斜率分别为,,当,则两直线互相垂直,所以C正确;
对于D中,当时,直线与直线为重合直线,所以D错误.
故选:C.
13.C
【分析】
利用平均数公式可求得结果.
【详解】
这两个班学生的数学总分为,故这两个班学生的数学平均分为.
故选:C.
14.C
【解析】
试题分析:所有基本事件有:,两胎均是女孩的基本事件只有,两胎均是女孩的概率,故选C.
考点:古典概型.
15.A
【分析】
观察折线图,结合选项逐一判断即可
【详解】
对于选项A,由图易知月接待游客量每年7,8月份明显高于12月份,故A错;
对于选项B,观察折线图的变化趋势可知年接待游客量逐年增加,故B正确;
对于选项C,观察折线图,各年的月接待游客量高峰期大致在7,8月份,故C正确;
对于D选项,观察折线图,各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳,故D正确.
故选:A
16.
【分析】
求出圆心与点的距离,再利用勾股定理即可得出答案.
【详解】
解:圆的圆心为,半径,
则圆心与点的距离,
所以切线长为.
故答案为:.
17..
【解析】
试题分析:由题意得,,
∴是以为首项,为公比的等比数列,∴,故填:.
考点:数列的通项公式及其运算.
18.
【分析】
将等式变形为,由此得出,展开后利用基本不等式可得出的最小值.
【详解】
在等式两边同时除以得,
,,,
当且仅当时,等号成立,
因此,的最小值为.
故答案为:.
【点睛】
本题考查利用基本不等式求最值,涉及的妙用,解题时将注意将定值条件化简变形,考查计算能力,属于中等题.
19..
【分析】
先在中用正弦定理求出,然后河的宽度为
【详解】
由题意可得在中,,且
所以由正弦定理得:
则
所以河的宽度为:
故答案为:
【点睛】
本题考查的是运用正弦定理解三角形,较简单.
20.(1),人(2)当发车时间间隔为分钟时,该线路每分钟的净收益最大,每分钟的最大净收益为元
【分析】
(1)由题意分别写出与时,的表达式,写成分段函数的形式,可得的表达式,可得的值;
(2)分别求出时,时,净收益为的表达式,并求出其最大值,进行比较可得净收益最大及收益最大时的时间.
【详解】
解:当时,
当时,设
解得,所以,
所以
(人)
当时,
当时
当时,
当且仅当时,即时, 取到最大值.
答:的表达式为
当发车时间间隔为分钟时,地铁的载客量为人.
当发车时间间隔为分钟时,该线路每分钟的净收益最大,每分钟的最大净收益为元.
【点睛】
本题主要考查分段函数解析式的求解及函数模型的实际应用,及利用基本不等式求解函数的最值,综合性大,属于中档题.
21.(1);(2).
【分析】
(1)由正弦定理可得,消去,可得,可得答案;
(2)由(1)所求A及,可得的值,再由余弦定理,可得b,c的值.
【详解】
解:(1)因为,
由正弦定理得:,
因为,所以.
因为A为锐角,所以.
(2)由,得:.
又的面积为,即.
所以.则.解得.
【点睛】
本题主要考查利用正弦定理、余弦定理解三角形,需注意公式的灵活运用.
22.(1)证明见解析;(2).
【分析】
(1)先证明CE //DA1,再利用线面平行的判定定理即可证明;
(2)利用线面垂直的判定定理的判定定理证明BF⊥平面CAA1D,然后求出直角梯形CAA1D的面积,利用锥体体积公式即可求解.
【详解】
(1)在三棱柱中,AA1 //CC1,AA1= CC1
因为D,E分别是CC1, AA1的中点,
所以CD//EA1,CD= EA1
所以四边形CEA1D是平行四边形.
所以CE //DA1
又因为CE平面BDA1,DA1 平面BDA1
所以CE//平面BDA1.
(2)设F为AC的中点,又△ABC为正三角形,
所以BF⊥AC.
在三棱柱ABC-A1B1C1中,AA1//BB1.
因为BB⊥平面ABC,所以AA1⊥平面ABC.
又BF平面ABC
所以AA1⊥BF.
又BF⊥AC,AA1∩AC=A
所以BF⊥平面CAA1D .
因此BF是四棱锥B-CAA1D的高,
因为正△ABC的边长为2,所以.
在三棱柱中,,
又D是CC1的中点,所以CD=1.
于是直角梯形CAA1D的面积
所以
所以四棱锥B-CAA1D的体试卷第1页,共3页
试卷第1页,共3页
同课章节目录
