北师大版2021--2022八年级(上)数学第五单元质量检测试卷C(含解析)
文档属性
| 名称 | 北师大版2021--2022八年级(上)数学第五单元质量检测试卷C(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1018.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 07:09:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2021-2022学年八年级(上)第五章二元一次方程组检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 方程组① ② ③ ④ 中,属于二元一次方程组的个数有
A. 个 B. 个 C. 个 D. 个
2. 下列方程组中,为三元一次方程组的是
A. B.
C. D.
3. 一副三角板按如图方式摆放,且 比 大 .若设 ,,则可得到的方程组为
A. B. C. D.
4. 数学课代表对全班 名学生业余时间数学小制作上交作品的情况进行了统计,统计结果如下表:
共上交作品 件,其中上交 件作品的有 人,上交 件作品的有 人,若 恰好是两条直线的交点,则这两条直线的解析式是
A. 与 B. 与
C. 与 D. 与
5. 同型号的甲、乙两辆车加满气体燃料后均可行驶 ,它们各自单独行驶并返回的最远距离是 .现在它们都从 地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回 地,而乙车继续行驶,到 地后再行驶返回 地,则 地最远可距离 地
A. B. C. D.
6. 在二元一次方程 的解中,当 时,对应的 的值是
A. B. C. D.
7. 如图是甲、乙两家商店销售同一种产品的销售价 (元)与销售量 (件)之间的函数图象.下列说法中,正确的是
①售 件时甲、乙两家售价一样;
②买 件时买乙家的合算;
③买 件时买甲家的合算;
④买乙家的 件售价约为 .
A. ①② B. ②③④ C. ②③ D. ①②③
8. 三元一次方程组 的解是
A. B. C. D.
9. 已知方程组 与 的值之和等于 ,则 的值为
A. B. C. D.
10. 二元一次方程组 的解是
A. B. C. D.
11. 用如图①中的长方形和正方形纸板分别作侧面和底面,做成如图②中的竖式和横式的两种无盖纸盒.现有 张正方形纸板和 张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,那么 的值可能是
A. B. C. D.
12. 篮球比赛中,每场比赛都要分出胜负,每队胜 场得 分,负一场扣 分,某队在 场比赛中得到 分,若设该队胜的场数为 ,负的场数为 ,则可列出方程组
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 一次函数的图象经过点 和 ,那么这个一次函数的解析式是 .
14. 在方程 中,已知 ,,则 .
15. 李师傅加工 个甲种零件和 个乙种零件的时间分别是固定的.现知道李师傅加工 个甲种零件和 个乙种零件共需 分钟;加工 个甲种零件和 个乙种零件共需 分钟.则李师傅加工 个甲种零件和 个乙种零件共需 分钟.
16. 若 是二元一次方程,则 , .
17. 若 是一个关于 ,, 的三元一次方程,那么 , .
18. “ 第二届中国,四明山国际越野跑挑战赛”将延期至 月 日开赛.小张和小李报名参加了这次活动.为了更好地参赛,赛前两人不断训练.每天下午他们定时定量训练,当小李跑了 米时,小张跑了 米,小李、小张在此后所跑的路程 (米)与时间 (秒)之间的函数关系如图所示,则训练跑的全程为 米.
三、解答题(共7小题;共60分)
19. (8分)班主任给参加数学和外语兴趣小组的学生购买课外读物,每人一本,共买回 本.数学课外读物每本 元,外语课外读物每本 元,另外已知购买两种课外读物用去的钱一样多.问参加数学与外语课外兴趣小组的学生各有多少人 共用去了多少钱
20(8分)若 ,且 求 的值.
21.(8分) 已知方程 ,用含 的代数式表示 ,并求 时 的值.
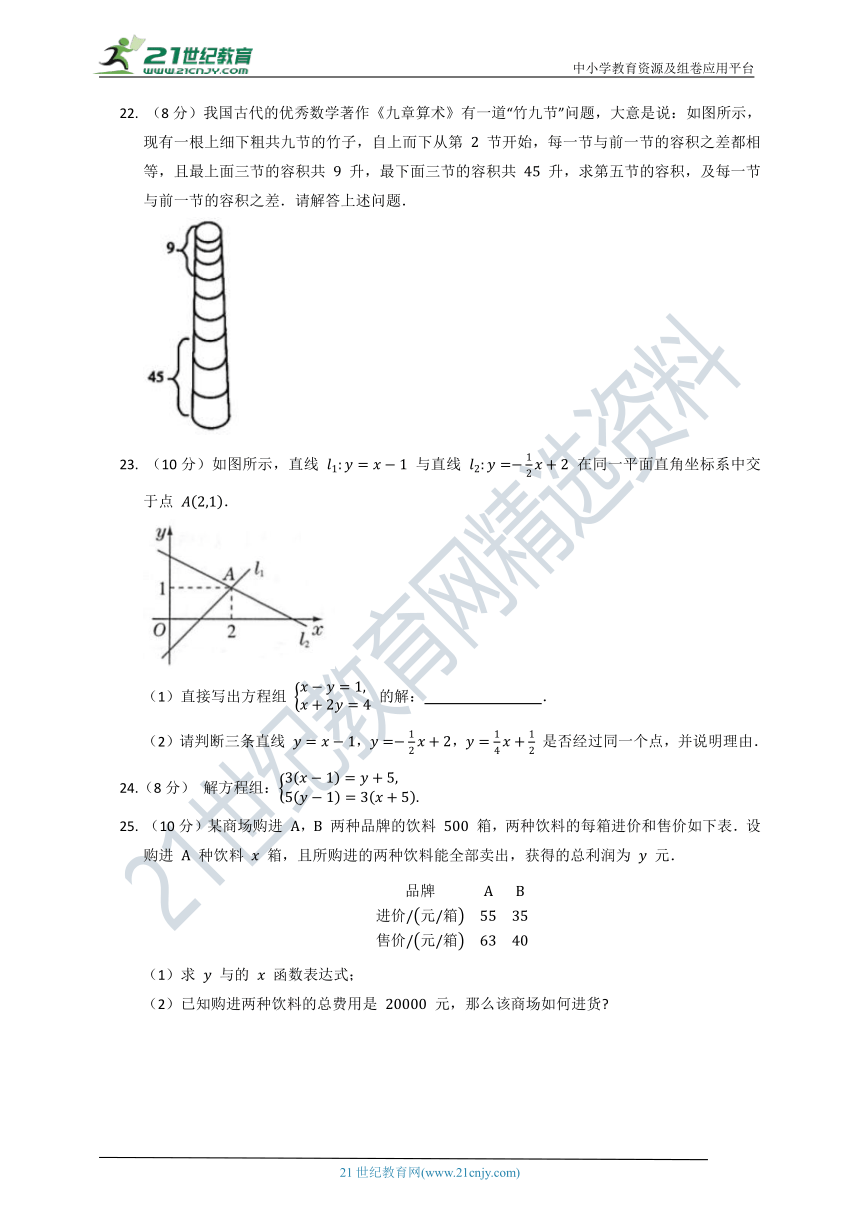
22. (8分)我国古代的优秀数学著作《九章算术》有一道“竹九节”问题,大意是说:如图所示,现有一根上细下粗共九节的竹子,自上而下从第 节开始,每一节与前一节的容积之差都相等,且最上面三节的容积共 升,最下面三节的容积共 升,求第五节的容积,及每一节与前一节的容积之差.请解答上述问题.
23. (10分)如图所示,直线 与直线 在同一平面直角坐标系中交于点 .
(1)直接写出方程组 的解: .
(2)请判断三条直线 ,, 是否经过同一个点,并说明理由.
24.(8分) 解方程组:
25. (10分)某商场购进 , 两种品牌的饮料 箱,两种饮料的每箱进价和售价如下表.设购进 种饮料 箱,且所购进的两种饮料能全部卖出,获得的总利润为 元.
(1)求 与的 函数表达式;
(2)已知购进两种饮料的总费用是 元,那么该商场如何进货
答案
第一部分
1. B
2. B 【解析】 A选项和C选项中都有四个未知数,而D选项中含未知数的项的最高次数是 ,
选项A,C,D 都不是三元一次方程组,
故选B.
3. D
4. D 【解析】根据共上交作品 件可得 ,
.
全班共有 名学生,
,
.
故选D.
5. B
【解析】设甲行驶到 地时返回,到达 地燃料用完,乙行驶到 地再返回 地时燃料用完,如图:
设 ,,根据题意得
解得
所以乙在 地时加注行驶 的燃料,则 的最大长度是 .
6. B 【解析】将 代入方程,得 ,则 .
故选B.
7. D
8. C 【解析】,
,,
把 , 代入 ,得 ,解得 ,
把 分别代入 ,,得 ,,
方程组的解为
9. B 【解析】
① ②得 ,
因为 与 的值之和等于 ,
所以 ,解得 .
10. D
【解析】由 得 ,把 代入 得 ,
所以 ,
所以原方程组的解是
11. A 【解析】设做竖式和横式的两种无盖纸盒分别 个, 个,
根据题意,得 两式相加,得 ,
因为 , 都是正整数,
所以 是 的倍数,
因为 ,,, 四个数中只有 是 的倍数,
所以 的值可能是 .故选A.
12. A
第二部分
13.
14.
15.
【解析】设李师傅加工 个甲种零件需 分钟,加工 个乙种零件需 分钟,
根据题意,得
,得 ,
,
.
16. ,
17. ,
【解析】根据题意得 ,,,解得 ,.
18.
【解析】设小李的速度为 米/秒,小张的速度为 米/秒,
由题意,得
解得
这次越野跑的全程为 米.
第三部分
19. 数学 人,外语 人,共用去 元.
20. .
21. , 时,.
22. 设第五节的容积为 升,每一节与前一节的容积之差为 升,依题意得
解得
答:第五节的容积为 升,每一节与前一节的容积之差为 升.
23. (1)
(2) 三条直线经过同一个点,理由如下:
解方程组 可得
把 代入 ,成立,
三条直线 ,, 经过同一个点 .
24.
去括号,得
① ②得:
解得:
把 代入①解得
所以这个方程组的解为
25. (1) 依题意得 .
(2) 根据题意,得
解得
.
该商场购进 , 两种品牌的饮料分别为 箱、 箱.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2021-2022学年八年级(上)第五章二元一次方程组检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 方程组① ② ③ ④ 中,属于二元一次方程组的个数有
A. 个 B. 个 C. 个 D. 个
2. 下列方程组中,为三元一次方程组的是
A. B.
C. D.
3. 一副三角板按如图方式摆放,且 比 大 .若设 ,,则可得到的方程组为
A. B. C. D.
4. 数学课代表对全班 名学生业余时间数学小制作上交作品的情况进行了统计,统计结果如下表:
共上交作品 件,其中上交 件作品的有 人,上交 件作品的有 人,若 恰好是两条直线的交点,则这两条直线的解析式是
A. 与 B. 与
C. 与 D. 与
5. 同型号的甲、乙两辆车加满气体燃料后均可行驶 ,它们各自单独行驶并返回的最远距离是 .现在它们都从 地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回 地,而乙车继续行驶,到 地后再行驶返回 地,则 地最远可距离 地
A. B. C. D.
6. 在二元一次方程 的解中,当 时,对应的 的值是
A. B. C. D.
7. 如图是甲、乙两家商店销售同一种产品的销售价 (元)与销售量 (件)之间的函数图象.下列说法中,正确的是
①售 件时甲、乙两家售价一样;
②买 件时买乙家的合算;
③买 件时买甲家的合算;
④买乙家的 件售价约为 .
A. ①② B. ②③④ C. ②③ D. ①②③
8. 三元一次方程组 的解是
A. B. C. D.
9. 已知方程组 与 的值之和等于 ,则 的值为
A. B. C. D.
10. 二元一次方程组 的解是
A. B. C. D.
11. 用如图①中的长方形和正方形纸板分别作侧面和底面,做成如图②中的竖式和横式的两种无盖纸盒.现有 张正方形纸板和 张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,那么 的值可能是
A. B. C. D.
12. 篮球比赛中,每场比赛都要分出胜负,每队胜 场得 分,负一场扣 分,某队在 场比赛中得到 分,若设该队胜的场数为 ,负的场数为 ,则可列出方程组
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 一次函数的图象经过点 和 ,那么这个一次函数的解析式是 .
14. 在方程 中,已知 ,,则 .
15. 李师傅加工 个甲种零件和 个乙种零件的时间分别是固定的.现知道李师傅加工 个甲种零件和 个乙种零件共需 分钟;加工 个甲种零件和 个乙种零件共需 分钟.则李师傅加工 个甲种零件和 个乙种零件共需 分钟.
16. 若 是二元一次方程,则 , .
17. 若 是一个关于 ,, 的三元一次方程,那么 , .
18. “ 第二届中国,四明山国际越野跑挑战赛”将延期至 月 日开赛.小张和小李报名参加了这次活动.为了更好地参赛,赛前两人不断训练.每天下午他们定时定量训练,当小李跑了 米时,小张跑了 米,小李、小张在此后所跑的路程 (米)与时间 (秒)之间的函数关系如图所示,则训练跑的全程为 米.
三、解答题(共7小题;共60分)
19. (8分)班主任给参加数学和外语兴趣小组的学生购买课外读物,每人一本,共买回 本.数学课外读物每本 元,外语课外读物每本 元,另外已知购买两种课外读物用去的钱一样多.问参加数学与外语课外兴趣小组的学生各有多少人 共用去了多少钱
20(8分)若 ,且 求 的值.
21.(8分) 已知方程 ,用含 的代数式表示 ,并求 时 的值.
22. (8分)我国古代的优秀数学著作《九章算术》有一道“竹九节”问题,大意是说:如图所示,现有一根上细下粗共九节的竹子,自上而下从第 节开始,每一节与前一节的容积之差都相等,且最上面三节的容积共 升,最下面三节的容积共 升,求第五节的容积,及每一节与前一节的容积之差.请解答上述问题.
23. (10分)如图所示,直线 与直线 在同一平面直角坐标系中交于点 .
(1)直接写出方程组 的解: .
(2)请判断三条直线 ,, 是否经过同一个点,并说明理由.
24.(8分) 解方程组:
25. (10分)某商场购进 , 两种品牌的饮料 箱,两种饮料的每箱进价和售价如下表.设购进 种饮料 箱,且所购进的两种饮料能全部卖出,获得的总利润为 元.
(1)求 与的 函数表达式;
(2)已知购进两种饮料的总费用是 元,那么该商场如何进货
答案
第一部分
1. B
2. B 【解析】 A选项和C选项中都有四个未知数,而D选项中含未知数的项的最高次数是 ,
选项A,C,D 都不是三元一次方程组,
故选B.
3. D
4. D 【解析】根据共上交作品 件可得 ,
.
全班共有 名学生,
,
.
故选D.
5. B
【解析】设甲行驶到 地时返回,到达 地燃料用完,乙行驶到 地再返回 地时燃料用完,如图:
设 ,,根据题意得
解得
所以乙在 地时加注行驶 的燃料,则 的最大长度是 .
6. B 【解析】将 代入方程,得 ,则 .
故选B.
7. D
8. C 【解析】,
,,
把 , 代入 ,得 ,解得 ,
把 分别代入 ,,得 ,,
方程组的解为
9. B 【解析】
① ②得 ,
因为 与 的值之和等于 ,
所以 ,解得 .
10. D
【解析】由 得 ,把 代入 得 ,
所以 ,
所以原方程组的解是
11. A 【解析】设做竖式和横式的两种无盖纸盒分别 个, 个,
根据题意,得 两式相加,得 ,
因为 , 都是正整数,
所以 是 的倍数,
因为 ,,, 四个数中只有 是 的倍数,
所以 的值可能是 .故选A.
12. A
第二部分
13.
14.
15.
【解析】设李师傅加工 个甲种零件需 分钟,加工 个乙种零件需 分钟,
根据题意,得
,得 ,
,
.
16. ,
17. ,
【解析】根据题意得 ,,,解得 ,.
18.
【解析】设小李的速度为 米/秒,小张的速度为 米/秒,
由题意,得
解得
这次越野跑的全程为 米.
第三部分
19. 数学 人,外语 人,共用去 元.
20. .
21. , 时,.
22. 设第五节的容积为 升,每一节与前一节的容积之差为 升,依题意得
解得
答:第五节的容积为 升,每一节与前一节的容积之差为 升.
23. (1)
(2) 三条直线经过同一个点,理由如下:
解方程组 可得
把 代入 ,成立,
三条直线 ,, 经过同一个点 .
24.
去括号,得
① ②得:
解得:
把 代入①解得
所以这个方程组的解为
25. (1) 依题意得 .
(2) 根据题意,得
解得
.
该商场购进 , 两种品牌的饮料分别为 箱、 箱.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
