人教版数学七年级上册_4.3.3 余角和补角 课件(35张)
文档属性
| 名称 | 人教版数学七年级上册_4.3.3 余角和补角 课件(35张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 10:46:02 | ||
图片预览






文档简介
(共35张PPT)
1.用度、分、秒表示:
1.38 °
50.675°
2.用度表示:
50°40′30″
1°22′48″
计算:
(1)7°49′+ 4°28′
(2) 9°18′ -6.5°
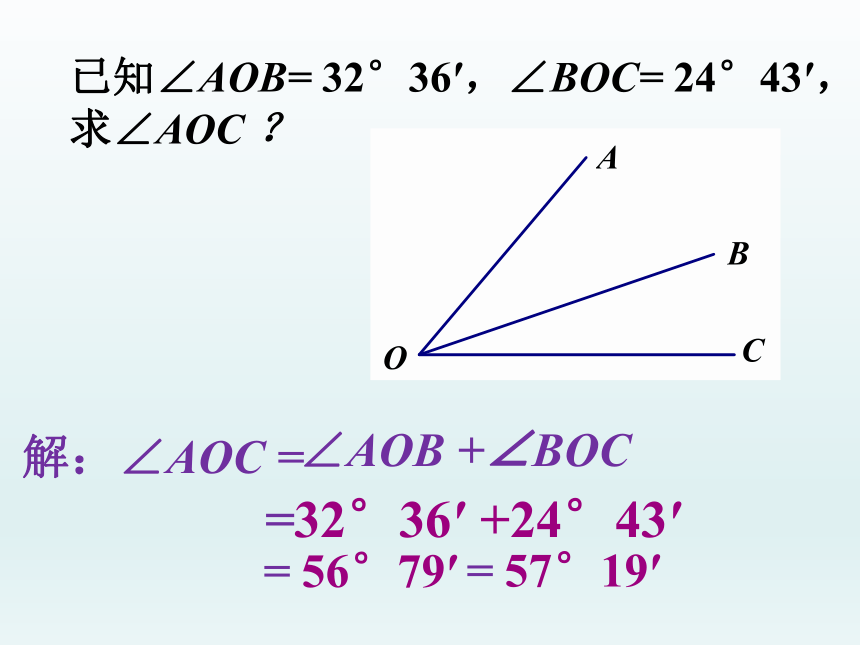
已知∠AOB= 32°36′,∠BOC= 24°43′,
求∠AOC ?
解:∠AOC =
∠AOB +∠BOC
= 56°79′
= 57°19′
=32°36′ +24°43′
P
A
O
B
1
2
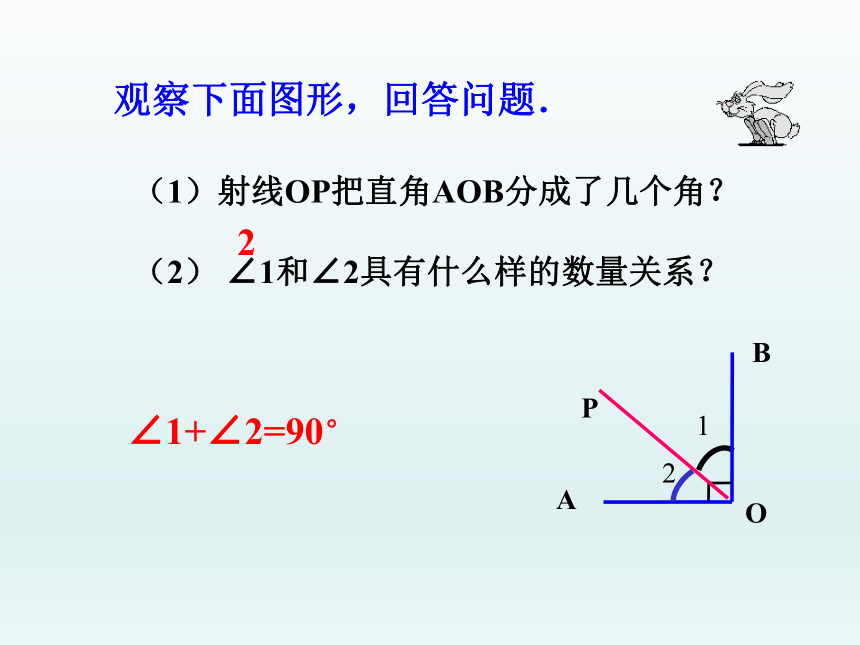
∠1+∠2=90°
观察下面图形,回答问题.
(1)射线OP把直角AOB分成了几个角?
(2) ∠1和∠2具有什么样的数量关系?
2
如果两个角的和等于90°(直角),那么称这两个角互为余角;简称两个角互余。
一、余角定义
也可以说其中一个角是另一个角的余角.
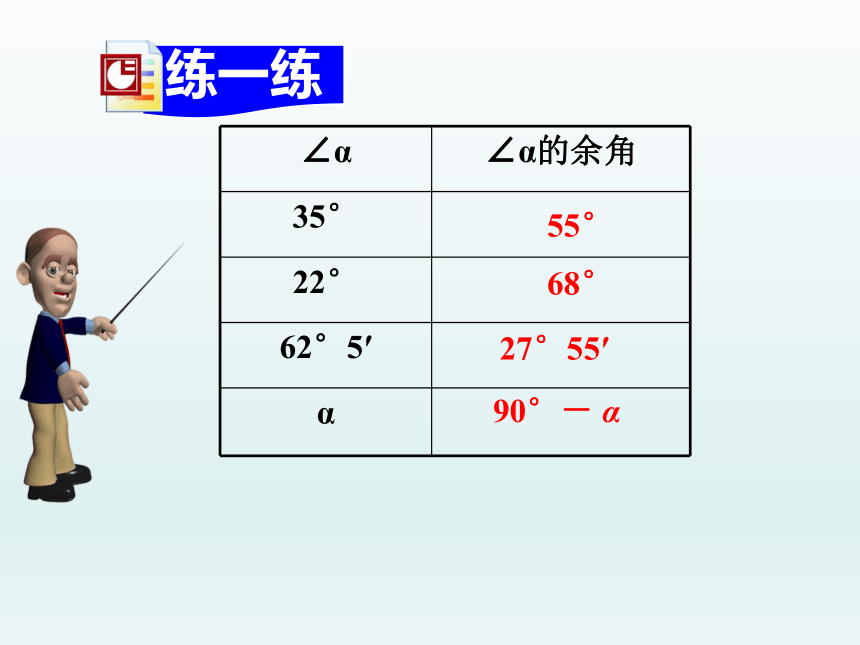
∠α ∠α的余角
35°
22°
62°5′
α
27°55′
55°
68°
90°- α
练一练
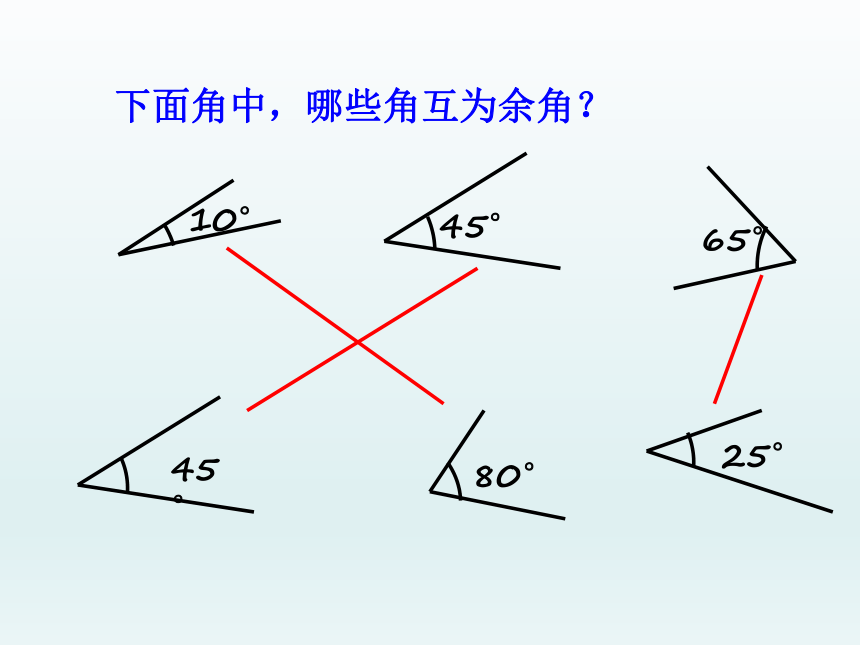
10°
45°
65°
45°
80°
25°
下面角中,哪些角互为余角?
观察下面图形,回答以下问题.
(1)射线OP把平角MON,分成了几个角?
(2)∠1和∠2具有什么样的数量关系?
∠1+∠2=180°
2
P
M
O
N
1
2
二、补角定义
如果两个角的和等于180°(平角),那么称这两个角互为补角;简称两个角互补。
也可以说其中一个角是另一个角的补角.
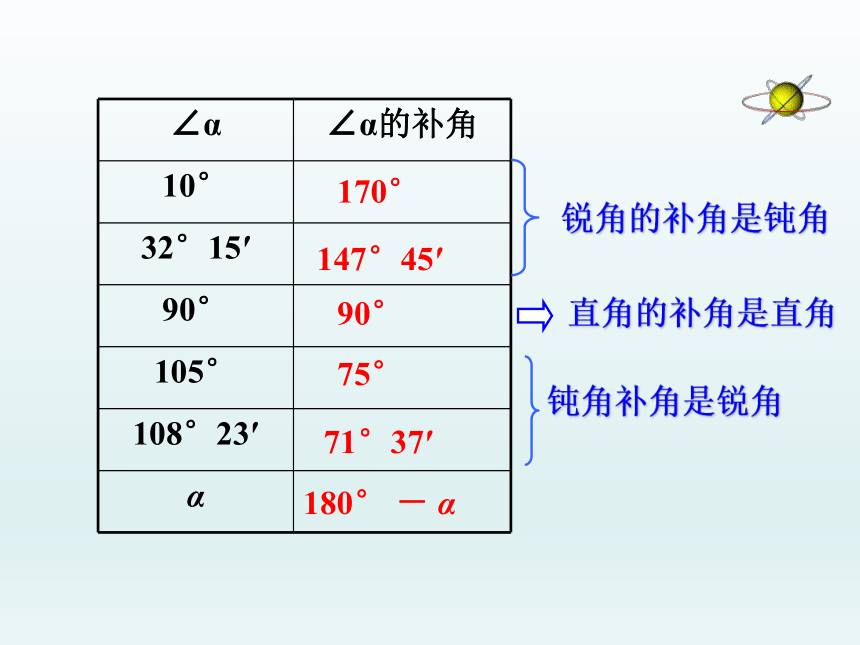
∠α ∠α的补角
10°
32°15′
90°
105°
108°23′
α
71°37′
170°
147°45′
90°
75°
180° - α
锐角的补角是钝角
直角的补角是直角
钝角补角是锐角
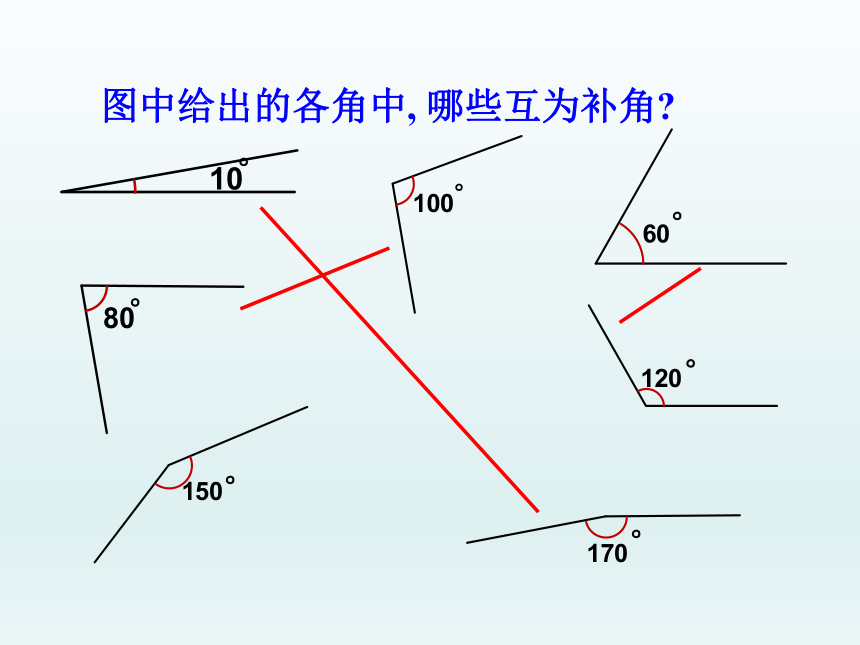
图中给出的各角中, 哪些互为补角
°
°
°
°
°
°
°
(1)图中互余的角是__________与___________.
(2)图中互补的角是__________与_______;_______与______.
M
P
O
N
Q
∠MOQ
∠QOP
∠MOP
∠PON
∠MOQ
∠QON
练一练
一个角的补角是这个角的余角的2.5倍,求这个角.
解:设这个角为x°.
180-x=2.5(90-x)
180-x=225-2.5x
2.5x-x=225-180
1.5x=45
x=30
答:这个角是30°
例题
判断:
1.锐角的余角一定是锐角.( )
2.一个锐角和一个钝角一定互为补角.( )
3.一个角的补角比这个角的余角大90°.( )
4.一个角的补角一定比这个角大.( )
√
×
√
×
练一练
2.如果两个角互补,其中一个角是另一个角的3.5倍,则这个角分别是( )
A.60°,210° B.20°,70°
C.40°,140° D.30°,150°
3.下列叙述正确的是( )
A.180°是补角
B.130°和50°互为补角
C.130°和 50°是补角
D.40°是50°的补角
C
B
4.(1)若∠α的补角与∠β的余角相等,求
∠α,∠β的关系.
解:因为180°- ∠α=90°- ∠β,
所以∠α- ∠β=90°.
所以∠α= ∠β+ 90°.
答: ∠α,∠β的关系为: ∠α= ∠β+ 90°.
∵∠AOB =90 °,
∴∠1+ ∠BOD = 90 °
∵∠COD = 90 °,
∴∠2+∠BOD =90 °
∴∠1+ ∠BOD = ∠2+ ∠BOD ,
∴ ∠1=∠2.
答:∠1=∠2.
∠AOB = 90 °,∠COD = 90 °
则∠1与∠2有什么数量关系?
A
O
B
C
D
1
2
答:∠1=∠2
同角的余角相等.
余角的性质1
知识要点
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
答:∠2=∠4
∵∠1 与∠2互余,
∴∠2= 90 °-∠1,
∵∠3与∠4互余 ,
∴∠4=90°- ∠3.
∵∠1=∠3,
∴90 °-∠1= 90°- ∠3
∴∠2=∠4.
余角的性质2
等角的余角相等.
知识要点
同角或等角的余角相等.
如图∠1 与∠2互补,∠3 与∠2互补 ,那么∠1与∠3相等吗?为什么?
∵∠1 与∠2互补,
∴ ∠1= 180 °-∠2;
∵∠3与∠2互补 ,
∴ ∠3= 180° -∠2.
∴ ∠1=∠3.
答:∠1=∠3
补角的性质1
同角的补角相等.
知识要点
答:∠1与∠3相等.
解: ∵∠1+∠2=180° ,
∴∠1=180 ° - ∠2;
∵∠3+∠4=180° ,
∴∠3= 180°- ∠4;
∵∠2=∠4,
∴ 180°- ∠2= 180°- ∠4,
∴ ∠1=∠3.
如图∠1+∠2=180°,∠3+∠4=180°,如果∠2=∠4,那么∠1与∠3有什么关系?为什么?
补角的性质2
等角的补角相等.
知识要点
同角或等角的补角相等.
互余 互补
对应
图形
数量
关系
性质
1
2
∠1+∠2=90°
∠1+∠2=180°
同角或等角的补角相等
同角或等角的余角相等
2
1
例 货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上, 在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
40°
B
C
10°
45°
D
例:下图中,OA是表示南偏西30 方向上的一条射线,仿照这条射线,画出表示下列方向的射线:(1)南偏东25 的射线OB;(2)北偏西50 的射线OC; (3)东北方向(即东偏北45 )的射线OD.
A
45°
25°
30°
50°
B
C
D
西
东
南
北
O
1.余角、补角的概念:
2.余角、补角的性质:
(1) 和为90°的两个角称互为余角;
(2) 和为180°的两个角称互为补角.
(1) 等角的余角相等;
(2) 等角的补角相等.
课堂小结
射线OC与射线OA所成的角是多少度?
射线OB与射线OD的所成的角是多少度?
A
45°
25°
30°
50°
B
C
D
西
东
南
北
O
100°
110°
1.6小时,12小时.
2.略.
3.(1)116°10′;(2)106°25′.
4.如果∠1=∠2,∠2=∠3,则∠1=∠3;
如果∠1>∠2,∠2>∠3,则 ∠1>∠3.
5.∠ABC=∠ACB=62°.
6.(1)∠AOB+∠BOC=∠AOC;
(2)∠AOC+∠COD=∠AOD;
(3)∠BOD-∠COD=∠BOC;
(4)∠AOD-∠BOD=∠AOB.
习题答案
7.延长AO或BO,先测量∠AOB的补角,然后
计算出∠AOB的大小.
8.10°与80°、30°与60°互为余角,10°与
170°、30°与150°、60°与120°、80°与
100°与为补角.
9.如图.
北
北偏东15°
东
南偏东60°
南
西南方向
西
北偏西30°
10.(1)∠BOD=70°;
(2)∠AOB=40°.
11.齿轮有15个齿,相邻两齿中心线的夹角是
24°,如果是22个齿轮,这个夹角约为
16°22′.
12.如图.
60°
30°
A
B
C
船的位置
13.(1)45°;(2)90°.
14.另外一个角等于135°,四边形的内角和等
于360°.
15.(1)这些和都等于360°;
(2)这些和等于360°,猜想:多边形外
角和等于360°.
1.用度、分、秒表示:
1.38 °
50.675°
2.用度表示:
50°40′30″
1°22′48″
计算:
(1)7°49′+ 4°28′
(2) 9°18′ -6.5°
已知∠AOB= 32°36′,∠BOC= 24°43′,
求∠AOC ?
解:∠AOC =
∠AOB +∠BOC
= 56°79′
= 57°19′
=32°36′ +24°43′
P
A
O
B
1
2
∠1+∠2=90°
观察下面图形,回答问题.
(1)射线OP把直角AOB分成了几个角?
(2) ∠1和∠2具有什么样的数量关系?
2
如果两个角的和等于90°(直角),那么称这两个角互为余角;简称两个角互余。
一、余角定义
也可以说其中一个角是另一个角的余角.
∠α ∠α的余角
35°
22°
62°5′
α
27°55′
55°
68°
90°- α
练一练
10°
45°
65°
45°
80°
25°
下面角中,哪些角互为余角?
观察下面图形,回答以下问题.
(1)射线OP把平角MON,分成了几个角?
(2)∠1和∠2具有什么样的数量关系?
∠1+∠2=180°
2
P
M
O
N
1
2
二、补角定义
如果两个角的和等于180°(平角),那么称这两个角互为补角;简称两个角互补。
也可以说其中一个角是另一个角的补角.
∠α ∠α的补角
10°
32°15′
90°
105°
108°23′
α
71°37′
170°
147°45′
90°
75°
180° - α
锐角的补角是钝角
直角的补角是直角
钝角补角是锐角
图中给出的各角中, 哪些互为补角
°
°
°
°
°
°
°
(1)图中互余的角是__________与___________.
(2)图中互补的角是__________与_______;_______与______.
M
P
O
N
Q
∠MOQ
∠QOP
∠MOP
∠PON
∠MOQ
∠QON
练一练
一个角的补角是这个角的余角的2.5倍,求这个角.
解:设这个角为x°.
180-x=2.5(90-x)
180-x=225-2.5x
2.5x-x=225-180
1.5x=45
x=30
答:这个角是30°
例题
判断:
1.锐角的余角一定是锐角.( )
2.一个锐角和一个钝角一定互为补角.( )
3.一个角的补角比这个角的余角大90°.( )
4.一个角的补角一定比这个角大.( )
√
×
√
×
练一练
2.如果两个角互补,其中一个角是另一个角的3.5倍,则这个角分别是( )
A.60°,210° B.20°,70°
C.40°,140° D.30°,150°
3.下列叙述正确的是( )
A.180°是补角
B.130°和50°互为补角
C.130°和 50°是补角
D.40°是50°的补角
C
B
4.(1)若∠α的补角与∠β的余角相等,求
∠α,∠β的关系.
解:因为180°- ∠α=90°- ∠β,
所以∠α- ∠β=90°.
所以∠α= ∠β+ 90°.
答: ∠α,∠β的关系为: ∠α= ∠β+ 90°.
∵∠AOB =90 °,
∴∠1+ ∠BOD = 90 °
∵∠COD = 90 °,
∴∠2+∠BOD =90 °
∴∠1+ ∠BOD = ∠2+ ∠BOD ,
∴ ∠1=∠2.
答:∠1=∠2.
∠AOB = 90 °,∠COD = 90 °
则∠1与∠2有什么数量关系?
A
O
B
C
D
1
2
答:∠1=∠2
同角的余角相等.
余角的性质1
知识要点
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
答:∠2=∠4
∵∠1 与∠2互余,
∴∠2= 90 °-∠1,
∵∠3与∠4互余 ,
∴∠4=90°- ∠3.
∵∠1=∠3,
∴90 °-∠1= 90°- ∠3
∴∠2=∠4.
余角的性质2
等角的余角相等.
知识要点
同角或等角的余角相等.
如图∠1 与∠2互补,∠3 与∠2互补 ,那么∠1与∠3相等吗?为什么?
∵∠1 与∠2互补,
∴ ∠1= 180 °-∠2;
∵∠3与∠2互补 ,
∴ ∠3= 180° -∠2.
∴ ∠1=∠3.
答:∠1=∠3
补角的性质1
同角的补角相等.
知识要点
答:∠1与∠3相等.
解: ∵∠1+∠2=180° ,
∴∠1=180 ° - ∠2;
∵∠3+∠4=180° ,
∴∠3= 180°- ∠4;
∵∠2=∠4,
∴ 180°- ∠2= 180°- ∠4,
∴ ∠1=∠3.
如图∠1+∠2=180°,∠3+∠4=180°,如果∠2=∠4,那么∠1与∠3有什么关系?为什么?
补角的性质2
等角的补角相等.
知识要点
同角或等角的补角相等.
互余 互补
对应
图形
数量
关系
性质
1
2
∠1+∠2=90°
∠1+∠2=180°
同角或等角的补角相等
同角或等角的余角相等
2
1
例 货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上, 在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
40°
B
C
10°
45°
D
例:下图中,OA是表示南偏西30 方向上的一条射线,仿照这条射线,画出表示下列方向的射线:(1)南偏东25 的射线OB;(2)北偏西50 的射线OC; (3)东北方向(即东偏北45 )的射线OD.
A
45°
25°
30°
50°
B
C
D
西
东
南
北
O
1.余角、补角的概念:
2.余角、补角的性质:
(1) 和为90°的两个角称互为余角;
(2) 和为180°的两个角称互为补角.
(1) 等角的余角相等;
(2) 等角的补角相等.
课堂小结
射线OC与射线OA所成的角是多少度?
射线OB与射线OD的所成的角是多少度?
A
45°
25°
30°
50°
B
C
D
西
东
南
北
O
100°
110°
1.6小时,12小时.
2.略.
3.(1)116°10′;(2)106°25′.
4.如果∠1=∠2,∠2=∠3,则∠1=∠3;
如果∠1>∠2,∠2>∠3,则 ∠1>∠3.
5.∠ABC=∠ACB=62°.
6.(1)∠AOB+∠BOC=∠AOC;
(2)∠AOC+∠COD=∠AOD;
(3)∠BOD-∠COD=∠BOC;
(4)∠AOD-∠BOD=∠AOB.
习题答案
7.延长AO或BO,先测量∠AOB的补角,然后
计算出∠AOB的大小.
8.10°与80°、30°与60°互为余角,10°与
170°、30°与150°、60°与120°、80°与
100°与为补角.
9.如图.
北
北偏东15°
东
南偏东60°
南
西南方向
西
北偏西30°
10.(1)∠BOD=70°;
(2)∠AOB=40°.
11.齿轮有15个齿,相邻两齿中心线的夹角是
24°,如果是22个齿轮,这个夹角约为
16°22′.
12.如图.
60°
30°
A
B
C
船的位置
13.(1)45°;(2)90°.
14.另外一个角等于135°,四边形的内角和等
于360°.
15.(1)这些和都等于360°;
(2)这些和等于360°,猜想:多边形外
角和等于360°.
